Уравнение пучка прямых

Совокупность прямых, проходящих через некоторую точку, называется пучком прямых с центром в этой точке.

Есл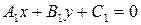и и 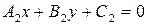- уравнения двух пересекающихся прямых, то уравнение

,

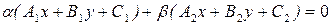где 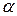и β любые числа, не равные нулю одновременно, называется уравнением пучка прямых, проходящих через точку пересечения данных прямых, причем при α=0 получаем уравнение второй прямой, при β=0 получаем уравнение первой прямой.

Пример. Написать уравнение пучка прямых, проходящих через точку пересечения прямых x-2y+3=0 и 2x+3y-1=0 и точку М₁(-1,2).

Решение. Запишем уравнение пучка прямых в виде

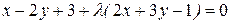
(Разделим обе части уравнения на )

Так как искомая прямая проходит через точку М₁(-1,2), то ее координаты удовлетворяют уравнению этой прямой.

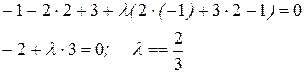
Подставив полученное значение λ в уравнение пучка, получим

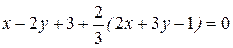или x+1=0

Ключевые слова: Угловой коэффициент, уравнение прямой, нормальный вектор, пучок прямых.