Рассмотрим условие условие 1, воспользуемся общим алгоритмом составления уравнения линии (структурная схема 1)
1. Дано:
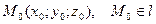
S (l, m, n) S? l
Составить уравнение прямой l
2 Выполним схематичный чертёж (рис. 14).
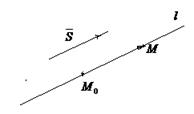
Рис.14
3. Возьмем на прямой l произвольную точку M(x, y, z).
4. Составим математическую модель задачи.
Точка M0? l по условию, точка M? l согласно алгоритму, тогда вектор 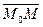 лежит на прямой l.
лежит на прямой l.
По условию задачи S?l, значит S? 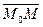 . Запишем условие параллельности векторов в векторной форме:
. Запишем условие параллельности векторов в векторной форме:
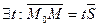
5. Запишем полученное уравнение в координатной форме, используя условия параллельности векторов в координатной форме.
Найдем координаты вектора 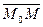 :
:
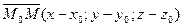 ,
,
т.к. вектора параллельные, то их координаты пропорциональные, тогда
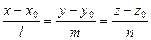 (10)
(10)
Полученные уравнения (10) называют каноническими уравнениями прямой.
Задача 10 Составить уравнение прямой проходящей через точку 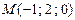 параллельно вектору
параллельно вектору 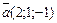 .
.
Решение
1. Установим точку, через которую проходит прямая: 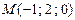 .
.
2. Найдем направляющий вектор S.
Так как вектор 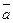 ? l, то его можно рассматривать как направляющий вектор прямой, т.е.
? l, то его можно рассматривать как направляющий вектор прямой, т.е. 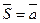 , тогда
, тогда 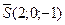 .
.
3. Составим уравнение прямой, используя канонические уравнения прямой (10):
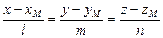 , Получим
, Получим
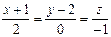 .
.
Ответ: 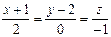
 2015-06-28
2015-06-28 18739
18739
