АЛГОРИТМ 7 Уравнение плоскости, проходящей через прямую и точку, не принадлежащую данной прямой Дано: 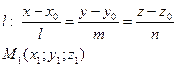 ________________________________ Составить уравнение плоскости α: ________________________________ Составить уравнение плоскости α: 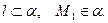 Решение Выполним схематичный чертеж (рис. 23) Решение Выполним схематичный чертеж (рис. 23) 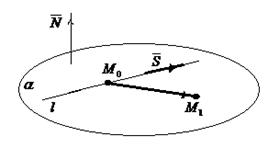 Рис.23 1 Рис.23 1 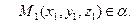 2 Найдем нормальный вектор плоскости α (рис. 23): 2 Найдем нормальный вектор плоскости α (рис. 23): 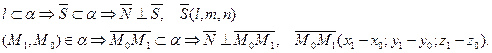 Нормальный вектор плоскости N как векторное произведение векторов: Нормальный вектор плоскости N как векторное произведение векторов: 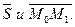 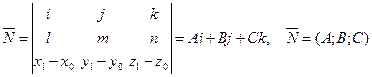 3 Подставим координаты точки 3 Подставим координаты точки  и вектора и вектора 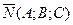 в «основное» уравнение (1) плоскости, получим в «основное» уравнение (1) плоскости, получим 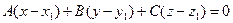 |
Задача 25 Составить уравнение плоскости, проходящей через точку 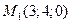 и прямую
и прямую 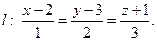
Решение
1 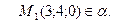
2 Найдем нормальный вектор плоскости α (рис. 32):
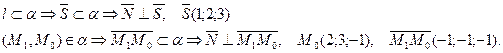
Нормальный вектор плоскости N найдем как векторное произведение векторов: 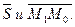
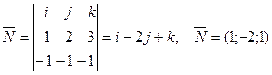
3 Подставим координаты точки 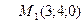 и вектора
и вектора 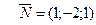 в уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
в уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору 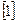 , получим
, получим
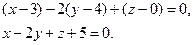
Ответ: 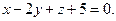
Выполните самостоятельно
Задача 25.1 Найти расстояние от точки 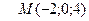 до плоскости, проходящей через прямую
до плоскости, проходящей через прямую 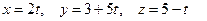 и точку
и точку 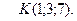
Ответ: точка М лежит в плоскости
3.4 Взаимное расположение прямой и плоскости в пространстве
Прямая и плоскость в пространстве могут пересекаться, быть параллельными или прямая лежит в плоскости.
|
|
|
Пусть прямая 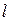 задана каноническими уравнениями:
задана каноническими уравнениями: 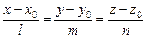 , а плоскость
, а плоскость 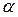 своим общим уравнением:
своим общим уравнением: 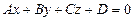
Структурная схема 4
 |
 2015-06-28
2015-06-28 9418
9418
