Списком можно задать лишь множества, содержащие несколько элементов. Задание типа
N = 1, 2, 3...
не список, а условное обозначение, допустимое, когда оно заведомо не вызывает разногласий.
Пример:
Определим А как множество все целых чисел х строго между 6 и 10. Это можно записать следующим образом:
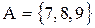
и прочитать как: “А- множество, содержащее 7, 8, 9”.
Множества часто рассматриваются как “неупорядоченные совокупности элементов”, хотя иногда полезно подчеркнуть, что, например,
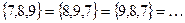 .
.
Мы не делаем никакой оговорки о порядке, в котором рассматриваются элементы, поэтому было бы неправильно допускать какой-либо определенный порядок.
Выясним далее, какие из приведенных определений верные:
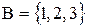
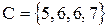
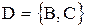 .
.
Если число членов множества В легко вычисляется, и среди элементов множества нет повторений, то определение верно.
Множество С также выглядит правильным, за исключением лишь того, что число 6 повторяется дважды. Мы можем проверить, принадлежит ли элемент или нет. Таким образом, это наиболее важное требование в определении множества выполнено. Следовательно, мы можем рассматривать эту запись как верную и эквивалентную 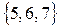 . Однако в этой ситуации возникают следующие проблемы. Если мы рассмотрим первоначальное определение Си выбросим одно из чисел 6 из множества, то мы, очевидно, будем иметь
. Однако в этой ситуации возникают следующие проблемы. Если мы рассмотрим первоначальное определение Си выбросим одно из чисел 6 из множества, то мы, очевидно, будем иметь 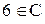 и
и 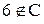 . Возникает противоречие. Поэтому мы будем рассматривать повторение символов в определении множеств как упоминание одного и того же символа, а его дублирование как недосмотр.
. Возникает противоречие. Поэтому мы будем рассматривать повторение символов в определении множеств как упоминание одного и того же символа, а его дублирование как недосмотр.
Определение D также справедливо. Заметим, что это множество множеств, такое, что оно имеет только два элемента, в частности, 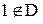 , даже если
, даже если 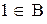 и
и 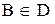 . Это легко проверить, так как
. Это легко проверить, так как 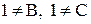 и только В и С являются элементами D.
и только В и С являются элементами D.
 2015-06-28
2015-06-28 2072
2072
