Для доказательства существования в системе свободных гармонических колебаний, необходимо было получить дифференциальное уравнение вида 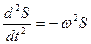 . Из дифференциального уравнения можно было определить циклическую частоту собственных колебаний ω и, следовательно, рассчитать период колебаний
. Из дифференциального уравнения можно было определить циклическую частоту собственных колебаний ω и, следовательно, рассчитать период колебаний 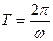 .
.
Можно предположить, что наличие в системе волнового процесса тоже описывается дифференциальным уравнением. Каков вид этого уравнения? Какие характеристики волнового процесса можно определить из этого уравнения?
Рассмотрим длинный твердый стержень, вдоль которого бежит продольная волна. Распространение продольной волны связано с возникновением в теле деформации растяжения-сжатия. Кроме того, все точки среды, по которой бежит волна, двигаются.
Пусть малый участок стержня длиной 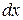 , расположенный между сечениями стержня с координатами x и
, расположенный между сечениями стержня с координатами x и 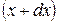 , испытывает деформацию растяжения.
, испытывает деформацию растяжения.
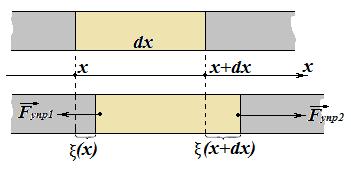
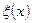 - смещение от положения равновесия точек, находящихся в левом сечении рассматриваемого участка стержня и имеющих координату х.
- смещение от положения равновесия точек, находящихся в левом сечении рассматриваемого участка стержня и имеющих координату х.
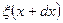 - смещение от положения равновесия точек, находящихся в правом сечении рассматриваемого участка стержня и имеющих координату
- смещение от положения равновесия точек, находящихся в правом сечении рассматриваемого участка стержня и имеющих координату 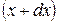 .
.
На выделенный участок стержня действуют силы упругости 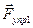 и
и 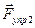 со стороны растянутых соседних участков стержня. Строго говоря, скорости и ускорения различных точек рассматриваемого участка разные, но ввиду малости участка
со стороны растянутых соседних участков стержня. Строго говоря, скорости и ускорения различных точек рассматриваемого участка разные, но ввиду малости участка 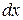 отличием скоростей и ускорений можно пренебречь. Запишем для выделенного участка стержня
отличием скоростей и ускорений можно пренебречь. Запишем для выделенного участка стержня 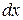 второй закон Ньютона:
второй закон Ньютона:
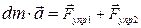 ,
,
где 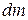 - масса рассматриваемого участка. В проекции на ОХ:
- масса рассматриваемого участка. В проекции на ОХ:
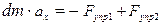
Масса рассматриваемого участка стержня 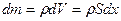 .
.
По определению проекция ускорения 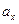 – это вторая производная от смещения
– это вторая производная от смещения 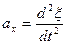 .
.
Силы упругости могут быть рассчитаны через напряжения в соответствующих сечениях: 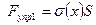 и
и 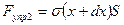 .
.
После подстановки получаем
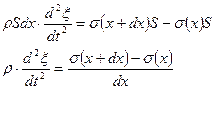
Очевидно, что отношение 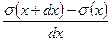 - это не что иное, как производная от напряжения по координате
- это не что иное, как производная от напряжения по координате 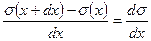 .
.
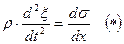
Согласно закону и напряжение прямо пропорционально относительному удлинению 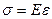 , где Е – модуль упругости вещества или модуль Юнга. Относительное удлинение ε – это отношение абсолютного удлинения к начальной длине образца. В нашем случае абсолютное удлинение равно
, где Е – модуль упругости вещества или модуль Юнга. Относительное удлинение ε – это отношение абсолютного удлинения к начальной длине образца. В нашем случае абсолютное удлинение равно 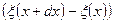 , а первоначальная длина рассматриваемого участка -
, а первоначальная длина рассматриваемого участка - 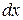 . Тогда относительное удлинение
. Тогда относительное удлинение 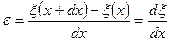 - производная от смещения по координате. Подставляем значение относительного удлинения в уравнение (*):
- производная от смещения по координате. Подставляем значение относительного удлинения в уравнение (*):
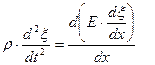
С учетом того, что модуль Юнга Е – это постоянная величина, получаем уравнение
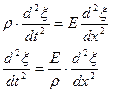
Нетрудно показать, что если ввести обозначение 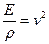 , то решением уравнения
, то решением уравнения 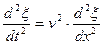 является уравнение плоской бегущей волны
является уравнение плоской бегущей волны 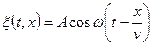 .
.
Подведем итоги.
1. Если для какой-либо системы удается получить дифференциальное уравнение вида 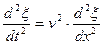 , то в системе распространяется волновой процесс. По этой причине дифференциальное уравнение
, то в системе распространяется волновой процесс. По этой причине дифференциальное уравнение 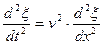 называется волновым уравнением.
называется волновым уравнением.
2. Волновое уравнение позволяет определить скорость волны v. Константа, стоящая в волновом уравнении перед второй производной по координате, - это величина, равная квадрату скорости волны.
В нашем случае получено значение скорости продольной волны в твердом теле 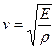 (как уже было сказано выше).
(как уже было сказано выше).
Энергия упругой волны
Процесс распространения упругой волны связан с вовлечением в колебательное движение частиц среды. Любое же колеблющееся тело обладает энергией, следовательно, можно говорить о передаче энергии колебательного движения от одних частиц среды другим. Иными словами, упругая волна переносит энергию.
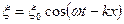 Пусть в некоторой области пространства вдоль оси ОХ распространяется плоская продольная волна. Ее уравнение имеет вид
Пусть в некоторой области пространства вдоль оси ОХ распространяется плоская продольная волна. Ее уравнение имеет вид
Рассмотрим малый элемент объема dV среды, в которой распространяется волна.
Частицы среды, находящиеся в выделенном нами объеме, двигаются, участвуя в колебательном движении, а значит, они обладают кинетической энергией.
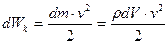 Поскольку выбранный нами элемент объема очень мал, можно считать, что все его точки имеют одинаковые скорости. Тогда кинетическая энергия выделенного объема может быть рассчитана как
Поскольку выбранный нами элемент объема очень мал, можно считать, что все его точки имеют одинаковые скорости. Тогда кинетическая энергия выделенного объема может быть рассчитана как
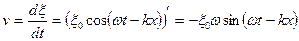 |
где r - плотность упругой среды, v – скорость всех точек выделенного нами объема. Скорость колебательного движения может быть найдена как производная от смещения по времени:
Тогда кинетическая энергия выделенного объема будет равна:
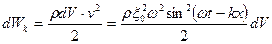 |
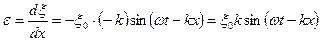 |
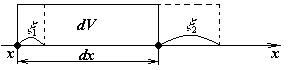 Распространение волны связано с деформацией упругой среды. Величина относительной деформации выделенного нами участка равна
Распространение волны связано с деформацией упругой среды. Величина относительной деформации выделенного нами участка равна 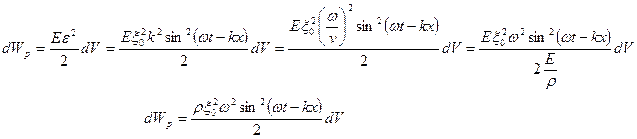
Потенциальная энергия упругой деформации выделенного объема dV:
Интересно!! Кинетическая и потенциальная энергии выделенного объема упругой среды (он, кстати, был выбран произвольно) одинаковы, более того, они меняются в одной фазе (в отличие от кинетической и потенциальной энергий колеблющегося маятника).
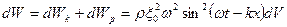 |
Полная энергия выделенного участка
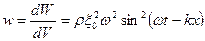 |
Плотность энергии волны (энергия единицы объема)
Видно, что плотность энергии любого участка среды, в которой распространяется волна, меняется с течением времени – переносится, передается от одних частиц другим.
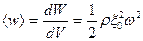 |
Среднее за период значение квадрата синуса равно ½, следовательно, средняя за период плотность энергии волны будет равна
Обычно, для характеристики волновых процессов пользуются понятием интенсивности волны. Интенсивностью волны называют энергию, переносимую волной за 1 секунду через поверхность площадью в 1 м2, расположенную перпендикулярно скорости распространения волны.
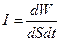 |
Рассчитаем интенсивность волны.
Через площадку dS за время dt будет перенесена энергия, заключенная в объеме цилиндра с основанием dS и высотой vdt. Поскольку размеры цилиндра очень малы, можно считать плотность энергии в каждой его точке одинаковой. Тогда: 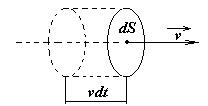
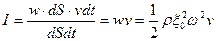 |
Интенсивность волны прямо пропорциональна:
1. плотности среды;
2. квадрату амплитуды волны (эта зависимость характерна для волнового процесса любой природы);
3. квадрату частоты волны;
4. скорости волны.
Если волна плоская, то ежесекундно в колебательное движение вовлекается одинаковое количество частиц, волновой фронт проходит через поверхность одинаковой площади. Это значит интенсивность волны везде одинаковая, следовательно, амплитуды колебания всех точек среды одинаковые.
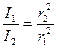 |
Если волна сферическая, то волновыми поверхностями для нее будут сферы. Энергия, переносимая волной за секунду через каждую сферу одинакова, а вот интенсивность волны будет убывать обратно пропорционально площади поверхности, т.е. обратно пропорционально расстоянию до источника волны:
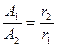 Тогда амплитуда колебания точек в сферической волне будет убывать обратно пропорционально расстоянию до источника волны:
Тогда амплитуда колебания точек в сферической волне будет убывать обратно пропорционально расстоянию до источника волны:
Выводы, полученные нами, справедливы и для поперечной волны.
Мы рассмотрели идеальный случай незатухающей волны. В реальной плоской волне амплитуда и интенсивность убывают с расстоянием по закону
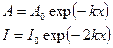
Энергия волны поглощается средой, в которой она распространяется.
 2015-07-14
2015-07-14 4122
4122
