Общие сведения о выборочном наблюдении

В связи с тем, что статистика имеет дело с массовыми совокупностями статистические исследования весьма трудоемки. Поэтому давно возникла мысль о замене сплошного наблюдения выборочным.

Выборочное наблюдение - это наиболее совершенный способ несплошного наблюдения, при котором обследуется не вся совокупность, а лишь ее часть, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.

При проведении выборочного наблюдения нельзя получить абсолютно точные данные. Как при сплошном, так как при выборочном наблюдении неизбежны ошибки, которые делятся на ошибки регистрации и ошибки репрезентативности. В свою очередь, ошибки репрезентативности бывают случайные и систематические.

Важнейшим условием применения выборочного метода является правильный отбор единиц совокупности, а именно:

а) строго объективный отбор единиц совокупности, при котором каждая из них получала бы абсолютно одинаковую возможность попасть в выборку;

б) достаточное количество отобранных единиц совокупности. При соблюдении этих условий выборка будет репрезентативной или представительной.

Вся совокупность единиц, из которой производится отбор, называется генеральной совокупностью и обозначается буквой N. Часть генеральной совокупности, попавшая в выборку, называется выборочной совокупностью и обозначается n.

Обобщающие показатели генеральной совокупности - средняя, дисперсная и доля - называются генеральными и соответственно обозначается 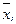σ, р, где p - доля или отношение числа единиц совокупности М, обладающих данным признаком ко всей численности генеральной совокупности, т.е. 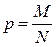. Те же обобщающие характеристики в выборочной совокупности обозначаются соответственно 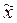, 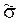², ω.

Теоретической основой выборочного метода является теорема П.Л.Чебышева, которая формулируется следующим образом: с вероятностью, сколь угодно близкой к единице (достоверности), можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности разность между выборочной средней и генеральной средней будет сколь угодно мала:

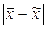< ε.

При практическом использовании теоремы Чебышева генеральную дисперсию 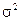, которая неизвестна, заменяют выборочной дисперсией.

Виды и схемы отбора

Формирование выборочной совокупности из генеральной может осуществляться по-разному. Различают следующие виды отбора: собственно-случайный; механический; типический; серийный; комбинированный.

1. Собственно-случайный отбор. Он ориентирован на выборку единиц из генеральной совокупности без всякого расчленения ее на части или группы. Либо применяется жеребьевка, либо используются таблицы случайных чисел.

2. Механический отбор. Он состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы), причем все единицы генеральной совокупности должны располагаться в определенном порядке. Размер интервала или группы равен обратной величине доли выборки (или количеству отбираемых единиц). Из каждой группы (интервала) берется только одна единица. Так, при 2%-ной выборке отбирается каждая 50-ая единица (1:0,02; или формируется 50 групп или интервалов), при 20%-ной выборке - каждая 5-я единица (1:0,2) и т. д.

3. Типический отбор. При его осуществлении вся генеральная совокупность делится на группы по типическому признаку, а затем в каждой группе проводится тот или иной отбор. Наиболее часто из каждой группы выбирается количество единиц, пропорциональное удельному весу группы в общей совокупности и как правило - механическим отбором. Такой отбор часто называют пропорциональным типическим отбором с механической выборкой.

4. Серийный отбор с равновеликими сериями состоит в выборке не отдельных единиц генеральной совокупности, а целых серий (гнезд). Попавшие в выборку серии подвергаются сплошному наблюдению. Сами серии могут формироваться различными методами и способами.

5. Комбинированный отбор. Все вышеперечисленные виды отбора комбинируются между собой.

Используя различные виды отбора, можно применить и различные схемы отбора: бесповторный отбор (схема невозвращенного шара)- после выбора какой-либо единицы она обратно в генеральную совокупность не попадает и не может быть выбрана снова; повторный отбор (схема возвращенного шара) - после выбора какой-либо единицы она вновь возвращается в генеральную совокупность и может быть выбрана снова.

Определение средних и предельных ошибок при различных видах отбора

Ошибка выборки 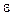- разность между характеристиками выборочной и генеральной совокупности.

Если 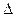представляет собой предел, которого не превосходит абсолютная величина 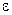то

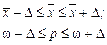
Ошибка выборки зависит от многих факторов, и, если из одной и той же генеральной совокупности можно сформировать бесконечное множество выборочных совокупностей, каждая из них даст и свою ошибку. Поэтому при выборочном наблюдении говорят о средней из возможных ошибок ( средняя или стандартная ошибка выборки), которую обозначают как .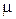

Величина 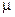прямо пропорциональна корню квадратному из дисперсии и обратно пропорциональна квадратному корню из объема выборочной совокупности;

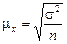, для доли, соответственно .

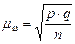Эти формулы справедливы для повторной схемы отбора. При бесповторном отборе вводится поправочный коэффициент, равный

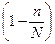, тогда .

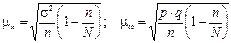В тех случаях, когда выборка небольшая этим множителем можно пренебречь, так как его значение близко к единице (обычно при ).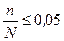

Для решения практических задач важна не средняя ошибка выборки, а пределы, за которые она не выйдет, т.е. говорят о предельной ошибке выборки.

Предельная ошибка выборки связана со средней ошибкой соотношением 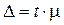, где t - коэффициент доверия, или t - статистика; t принимает значения 1, 2 или 3 и связан с вероятностью достижения заданного предела. Если t =1 это значит, что вероятность того, что ошибка выборки не превысит заданного значения, равна 0,683 или 68,3%. При t =2 - P =0,954 или 95,4%; t =3 - P =0,997 или 99,7%.

Таким образом, предельная ошибка выборки зависит от трех факторов: дисперсии 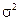, объема выборки n, и коэффициента доверия t. Формулы для определения предельных ошибок при различных видах и схемах отбора приведены в табл. 6

Таблица 6

Определение предельной ошибки выборки при различных видах отбора

	Схема отбора	Предельная ошибка выборки
	для средней	для доли
Собственно - случайный и механический отбор
Повторный отбор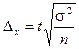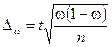
Бесповторный отбор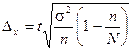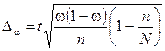
Типический отбор
Поторный отбор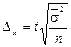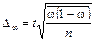
Бесповторный отбор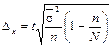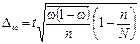
Серийный отбор
Повторный отбор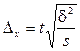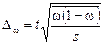
Бесповторный отбор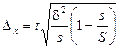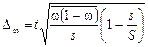

Виды и формы взаимосвязи между явлениями

Одной из важнейших задач статистики является изучение, измерение и количественное выражение взаимосвязи между явлениями общественной жизни, установленной на основе качественного анализа.

Различают два вида связей: функциональную и корреляционную, обусловленные двумя типами закономерностей: динамическими и статистическими.

Для явлений, в которых проявляются динамические закономерности, характерна жесткая, механическая причинность, которая может быть выражена в виде уравнения, четкой зависимости и т.д. Такая зависимость называется функциональной. При функциональной связи каждому значению одной величины (аргумента) соответствует одно или несколько вполне определенных значений другой величины (функции).

В общественных процессах, в которых проявляются статистические закономерности, нет строгой зависимости между причиной и результатом и обычно не представляется возможным выявить строгую зависимость.

Связь, при которой каждому значению аргумента соответствует не одно, а несколько значений функции и между аргументом и функциями нельзя установить строгой зависимости называется корреляционной. Корреляционная зависимость проявляется только в средних величинах и выражает числовое соотношение между ними в виде тенденции к возрастанию или убыванию одной переменной величины при возрастании или убывании другой.

По направлению различают прямую и обратную связи.

По аналитическому выражению корреляционная связь может быть прямолинейной и криволинейной.

Основные приемы изучения взаимосвязей

а) Метод параллельных рядов. Чтобы установить связь между явлениями достаточно расположить полученные в результате сводки и обработки материалы в виде параллельных рядов и сопоставить их между собой.

б) Балансовый метод. Для характеристики взаимосвязи между явлениями в статистике широко применяется балансовый метод. Сущность его заключается в том, что данные взаимосвязанных показателей изображаются в виде таблицы и располагаются таким образом, чтобы итоги между отдельными частями были равны, т.е. чтобы был баланс. Балансовый метод используется для характеристики взаимосвязи между производством и распределением продуктов, денежными доходами и расходами населения и т.д.

в) Метод аналитических группировок. При наличии массовых статистических данных для изучения и измерения взаимосвязей социально-экономических явлений широко пользуются методом аналитических группировок. Аналитические группировки позволяют установить наличие связи между двумя и более признаками и ее направление. Метод группировок сочетается с методом средних и относительных величин.

г) Дисперсионный анализ. Аналитические группировки при всей своей значимости не дают количественного выражения тесноты связи между признаками. Эта задача решается при помощи дисперсионного и корреляционного анализов.

Дисперсионный анализ дает, прежде всего, возможность определить роль систематической и случайной вариаций в общей вариации и, следовательно, установить роль изучаемого фактора в изменении результативного признака. Для этого пользуются правилом сложения дисперсий.

Корреляционный анализ

Определение формы связи

Изучение взаимосвязей между признаками статистической совокупности заключается в определении формы и количественной характеристики связи, а также степени тесноты связи. Корреляционный анализ и решает эти двеосновныезадачи.

Первая задача заключается в определении формы связи, т.е. в установлении математической формы, в которой выражается данная связь.

Предварительный этап при установлении формы связи заключается в теоретическом анализе изучаемого явления, а также в представлении искомой связи графически. График, построенный по исходным данным, позволяет приблизительно определить: есть ли какая-то связь между явлениями; ее направление (прямая или обратная); примерную тесноту связи (естественно, что при графическом анализе используются только две переменные).

Применение методов корреляционного анализа дает возможность выражать связь между признаками аналитически - в виде уравнения - и придавать ей количественное выражение.

Другими словами необходимо найти зависимость вида y=f(x), причем в качестве функции f(x) могут быть

полином 1-го порядка -

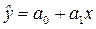
полином 2-го порядка -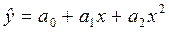

степенная функция -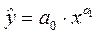

гиперболическая функция -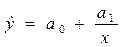

(могут быть использованы и другие виды функций).

Неизвестные параметры функций (аналитических уравнений связи) находятся методом наименьших квадратов, сущность которого в следующем: сумма квадратов отклонений фактических данных от выровненных должна быть наименьшей (см. рисунок):

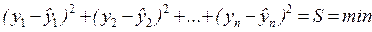
или

y

x

Ù

y

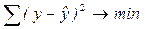
Отклонение фактических уровней от выровненных

Измерение тесноты связи

При изучении корреляционной связи важно выяснить не только форму, но и тесноту связи между факторным и результативным признаком. Для этого (при прямолинейной связи) рассчитывается показатель, называемый парным линейным коэффициентом корреляции 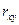, вычисляемый по формуле

.

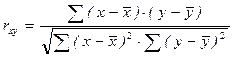Коэффициент корреляции принимает значение от -1 до +1, причем если 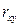>0, то корреляция прямая, если 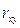<0, то корреляция обратная, а если 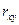=0, то корреляция отсутствует полностью.

В зависимости от того, насколько 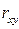приближается к единице, различают связь слабую, умеренную, заметную, высокую, тесную и весьма тесную.

Коэффициент корреляции может быть исчислен и по следующей формуле ,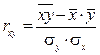

где 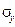- среднее квадратическое отклонение результативного признака;

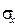- среднее квадратическое отклонение факторного признака.

Зная линейный коэффициент корреляции, можно определить и параметры уравнения регрессии вида 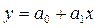потому что:

.

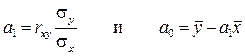Коэффициент корреляции 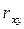применяется только в тех случаях, когда между явлениями существует прямолинейная связь. Если же связь криволинейная, то пользуются коэффициентом корреляции, вычисляемым по формуле

,

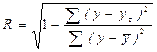где y - исходные значения результативного показателя;

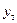-теоретические значения;

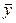-среднее значение y.

Имея среднее значение дисперсий, коэффициент корреляции можно вычислить как

,

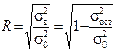где 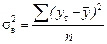- факторная (межгрупповая) дисперсия или дисперсия воспроизводимости;

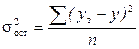- случайная (средняя из внутригрупповых) дисперсия или остаточная дисперсия; 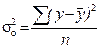- общая дисперсия.

Коэффициент корреляции по своему абсолютному значению находится в пределах от 0 до 1.

Если коэффициент корреляции возвести в квадрат и выразить в процентах, получим показатель, называемый коэффициентом детерминации

D = R ²∙100%.

Он показывает, на сколько процентов изменение результативного фактора зависит от изменения факторного признака. Коэффициент детерминации является наиболее конкретным показателем, так как он отвечает на вопрос о том, какая доля в общем результате зависит от фактора, положенного в основании группировки.

Примерные вопросы для собеседования

1. Ряды распределения: понятие, виды, элементы. Графическое изображение рядов распределения.

2. Выборочный метод: причины применения, решаемые задачи. Выборочная совокупность: способы отбора, виды выборки, ошибка выборки.

3. Корреляционно-регрессионный анализ (КРА): понятие, условия применения, задачи КРА.

4. Вычисление и интерпретация параметров парной линейной корреляции.

Тематика, выносимая на самостоятельное изучение (в объеме 9 часов):

1. Показатели вариации и способы их расчета.

2. Определение необходимой численности выборки

3. Множественная корреляция.

4. Методы измерения тесноты связи.