В систему уравнения Максвелла входят частные производные пот четырем независимым переменным − координаты и время. Для упрощения решения было бы весьма целесообразно исключить одну из этих переменных. Такая операция оказывается действительно возможной, если рассматриваемый электромагнитный процесс является монохроматическим, т.е. изменение полей во времени представляется гармоническими колебаниями с некоторой частотой. В буквальном переводе «монохроматический» означает «одноцветный», это название взято из оптики: известно, что каждому чистому цвету соответствуют колебания одной определенной частоты. Помимо того, что случай монохроматических колебаний наиболее часто встречается на практике, знание поведения поля на всех частотах позволяет воссоздать любой закон изменения во времени, воспользовавшись преобразованием Фурье.
Вектор, проекции которого на оси координат изменяются по гармоническому закону, называется гармоническим. Тогда
 .
.
Здесь  ,
,  ,
,  − амплитуды проекции вектора на координатные оси,
− амплитуды проекции вектора на координатные оси,  ,
,  ,
,  −начальные фазы проекций вектора,
−начальные фазы проекций вектора,  − круговая частота. Все перечисленные величины являются вещественными.
− круговая частота. Все перечисленные величины являются вещественными.
С течением времени конец вектора  описывает в пространстве замкнутую кривую, причем можно показать, то данная кривая является эллипсом. Положение плоскости эллипса и его эллиптичность определяются как амплитудами, так и фазами отдельных составляющих.
описывает в пространстве замкнутую кривую, причем можно показать, то данная кривая является эллипсом. Положение плоскости эллипса и его эллиптичность определяются как амплитудами, так и фазами отдельных составляющих.
Анализ гармонических процессов существенно упрощается при использовании метода комплексных амплитуд. В этом случае вместо любой скалярной функции (например, компонент вектора  ), которая изменяется по гармоническому закону:
), которая изменяется по гармоническому закону:
 ,
,
вводится в рассмотрение комплексная функция:

Величина
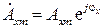
называется комплексной амплитудой функции  или комплексной амплитудой проекции вектора
или комплексной амплитудой проекции вектора  . Признак комплексной амплитуды обозначается точкой сверху. Если к значению комплексной амплитуды применить формулу Эйлера и взять вещественную часть, то получим исходную функцию
. Признак комплексной амплитуды обозначается точкой сверху. Если к значению комплексной амплитуды применить формулу Эйлера и взять вещественную часть, то получим исходную функцию  .
.
 ;
;
 .
.
Аналогично, вместо вектора  можно ввести в рассмотрение комплексный вектор
можно ввести в рассмотрение комплексный вектор
 .
.
Вводя комплексные амплитуды для каждой из компонент, получим

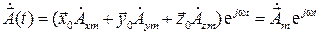 .
.
Здесь величина

называется комплексной амплитудой вектора  . Таким образом, комплексная амплитуда вектора представляет собой сумму комплексных амплитуд проекций вектора, умноженных на соответствующие координатные орты. Комплексный вектор представляет собой произведение функции координат – комплексной амплитуды
. Таким образом, комплексная амплитуда вектора представляет собой сумму комплексных амплитуд проекций вектора, умноженных на соответствующие координатные орты. Комплексный вектор представляет собой произведение функции координат – комплексной амплитуды  и функции времени
и функции времени 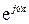 :
:

Для перехода от комплексного вектора к гармоническому надо от комплексного вектора взять реальную часть:
 .
.
Экспоненциальные множители с мнимыми показателями стоящие при комплексных амплитудах, характеризуют исключительно фазовые, а не пространственные соотношения между величинами.
Метод комплексных амплитуд значительно упрощает технику преобразований при получении решений дифференциальных уравнений в частных производных. Все члены линейного дифференциального уравнения оказываются умноженными на 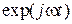 . Опуская этот множитель, получим уравнение относительно комплексной амплитуды, не зависящей от времени. Если в результате решения уравнения комплексная амплитуда определена, то для получения искомой физической величины нужно лишь умножить комплексную амплитуду на
. Опуская этот множитель, получим уравнение относительно комплексной амплитуды, не зависящей от времени. Если в результате решения уравнения комплексная амплитуда определена, то для получения искомой физической величины нужно лишь умножить комплексную амплитуду на 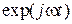 и отделить вещественную часть.
и отделить вещественную часть.
Почему такой подход правомерен? Дело в том, что если существует решение некоторого линейного уравнения (алгебраического, дифференциального или интегрального) в виде комплексного представления, то этому уравнению удовлетворяют в отдельности его вещественная и мнимая части, а тем самым решением является рассматриваемая физическая величина.
Определение комплексных функций во многих случаях оказывается проще определения исходных функций. Это объясняется тем, что дифференцирование комплексной функции по времени сводится к ее умножению на  , а интегрирование − делению на
, а интегрирование − делению на  :
:
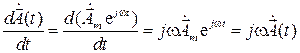 ,
,
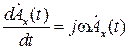 ,
,

 .
.
 2015-10-22
2015-10-22 4355
4355