ВЕКТОРНАЯ АЛГЕБРА
В математике и ее приложениях различают два типа величин: векторные и скалярные.
Скалярной называется величина, которая полностью определяется числом, выражающим отношение величины к соответствующей единице измерения.
Векторной называется величина, для полного определения которой нужно задать кроме численного значения еще направление в пространстве.
Вектором называется направленный отрезок прямой, с начальной точкой А и конечной точкой В.
Вектор называется свободным, если для него заданы направление и длина, а положение в пространстве не фиксировано. Т.Е. при параллельном переносе он не меняется.
Два вектора  и
и  равны, если:
равны, если:
1) они сонаправлены (имеют одинаковое направление);
2) длины отрезков  и
и  равны.
равны.
Нулевым называется вектор, начало и конец которого совпадают.
Длиной вектора  называется длина отрезка
называется длина отрезка  .
.
Единичным вектором или орт-вектором называется вектор единичной длины.
Векторы  и
и  называются коллинеарными, если они лежат на одной или параллельных прямых. При этом они могут быть сонаправлены (имеют одно направление) или противонаправлены (имеют противоположное направление).
называются коллинеарными, если они лежат на одной или параллельных прямых. При этом они могут быть сонаправлены (имеют одно направление) или противонаправлены (имеют противоположное направление).
Векторы называются компланарными, если они лежат на одной или параллельных плоскостях.
Линейные операции над векторами.
К линейным относятся операции сложения векторов и умножение вектора на число.
Суммой векторов  и
и  называется вектор, полученный по правилу сложения векторов:
называется вектор, полученный по правилу сложения векторов:
А) если совместить начала векторов, то суммой будет вектор, начало которого совпадает с началами векторов, а конечная точка - противоположная вершина параллелограмма, сторонами которого будут  и
и  ;
;
В) если совместить начало второго вектора и конечную точку первого, то сумма – вектор, начало которого совпадает с начальной точкой первого вектора, а конечная – с конечной точкой второго.
Суммой конечного числа векторов служит замыкающий вектор:
Вектор  называется противоположным вектору
называется противоположным вектору  , если их длины совпадают, а направления противоположны.
, если их длины совпадают, а направления противоположны.
Разностью векторов  и
и  называется вектор
называется вектор  , который является суммой векторов
, который является суммой векторов  и -
и -  . Вектор
. Вектор  направлен к концу вектора
направлен к концу вектора  , если
, если  и
и  приведены к одному началу.
приведены к одному началу.
Произведением вектора  на число
на число  называется вектор
называется вектор  , для которого:
, для которого:
1) длина в  раз больше:
раз больше: 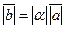
2) направления совпадают, если  и противоположны, если
и противоположны, если 
Для любого ненулевого вектора  можно определить орт вектора:
можно определить орт вектора:
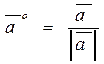
Введенные операции называются линейными и обладают рядом свойств:
1) Сложение векторов коммутативно: 
2) Сложение векторов ассоциативно: 
3) 
4) 
5) Умножение вектора на число ассоциативно: 
6) 
7) Умножение вектора на число дистрибутивно относительно сложения чисел: 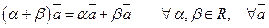
8) Умножение вектора на число дистрибутивно относительно сложения векторов: 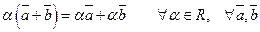
Множество векторов, удовлетворяющих этим свойствам, образуют линейное векторное пространство 
Проекция вектора.
Ось – прямая, на которой задано направление.
Углом между двумя векторами (вектором и осью, двумя осями) называется меньший угол  , на который нужно повернуть один вектор (ось), чтобы он совпал по направлению с другим вектором (осью).
, на который нужно повернуть один вектор (ось), чтобы он совпал по направлению с другим вектором (осью).
Очевидно,  .
.
Проекцией вектора  на ось
на ось 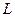 называется длина отрезка
называется длина отрезка 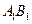 , заключенного между ортогональными проекциями начала и конца вектора на эту ось, взятая со знаком «+», если направление оси и направление от
, заключенного между ортогональными проекциями начала и конца вектора на эту ось, взятая со знаком «+», если направление оси и направление от  к
к  совпадают и со знаком «-», если не совпадают.
совпадают и со знаком «-», если не совпадают.
Из рисунка видно, что проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью:
 (1)
(1)
Направленный отрезок  называется ортогональной составляющей вектора
называется ортогональной составляющей вектора  по оси
по оси 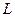 . Очевидно,
. Очевидно, 
 (2)
(2)
СВОЙСТВА проекции:
1) 
2) 
 2015-10-22
2015-10-22 10575
10575







