Предпосылки метода наименьших квадратов

Метод наименьших квадратов (МНК) позволяетпостроить уравнение регрессии на основе минимизации суммы квадратов отклонений: , или .

Поэтому важно исследовать поведение остаточных величин регрессии – ε. Они должны отвечать определенным критериям:

1. Несмещенность – означает, что математическое ожидание остатков равно нулю: , т.е. при большом числе наблюдений остатки не будут накапливаться и найденный параметр регрессии b можно рассматривать как среднее значение из возможного большого количества несмещенных оценок. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным выборкам.

2. Эффективность – оценки считаются эффективными, если они характеризуются наименьшей дисперсией.

3. Состоятельность – характеризует увеличение точности оценок с увеличением объема выборки.

Условия, необходимые для получения несмещенных, эффективных и состоятельных оценок, представляют собой предпосылки МНК (условия Гаусса-Маркова), соблюдение которых желательно для получения достоверных результатов регрессии.

Выделяют пять предпосылок МНК:

ü случайный характер остатков;

ü нулевая средняя величина остатков, не зависящая от х;

ü гомоскедастичность;

ü отсутствие автокорреляции остатков;

ü нормальное распределение остатков.

I предпосылка МНК. Прежде всего проверяется случайный характер остатков ε. С этой целью строится график их зависимости от теоретических значений результативного признака :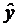

Рис. 2.1. Зависимость случайных остатков от теоретическихзначений

 

Если на графике нет направленности в расположении точек, то остатки представляют собой случайные величины и МНК оправдан.

Возможны следующие случаи, если зависит от , то:

1) остатки не случайны

2) остатки не имеют постоянной дисперсии

3) остатки носят систематический характер

 

В этих случаях необходимо либо применять другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки не будут случайными величинами.

II предпосылка МНК. Нулевая средняя величина остатков, не зависящая от х, т.е. . С целью проверки выполнения этой предпосылки строится график зависимости случайных остатков от факторов , включенных в регрессию (рис. 2.3).

Рис. 2.3. Зависимость величины остатков от величины фактора .

 

Если расположение остатков на графике не имеет направленности, то они независимы от значений . Если же график показывает наличие зависимости и , то модель неадекватна.

III предпосылка МНК. Гомоскедастичность – это однородность относительно дисперсии, т.е. дисперсия остатков одинакова для каждого значения х. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность (неоднородность относительно дисперсии).

Примеры гетероскедастичности:

а – дисперсия остатков растет

по мере увеличения б – дисперсия остатков достигает

максимальной величины при средних

значениях переменной и уменьшается

при минимальных и максимальных значениях

в – максимальная дисперсия остатков при малых значениях и дисперсия остатков однородна по мере увеличения значений

Для проверки выполнения предпосылки МНК о гомоскедастичности остатков используются различные методы:

1. Тест Гольдфельда-Квандта. Процедура применения теста Гольдфелда-Квандта состоит из следующих шагов:

1) наблюдения упорядочиваются по возрастанию фактора хi;

2) из рассмотрения исключаются С центральных наблюдений. При этом должно выполняться условие (n-С)/2 > р, где p – число оцениваемых параметров (авторами метода рекомендовано для случая одного фактора при n =30 принимать С=8, а при n =60 принимать С =16);

3) совокупность из n-C наблюдений разделяется на две группы (соответственно с большими и малыми значениями фактора х) и по каждой группе определяется уравнение регрессии;

4) определяются остаточные суммы квадратов для первой () и второй () групп и находится их отношение: R = , где S2 >S1;

5) нулевая гипотеза о гомоскедастичности остатков отвергается, если выполнено условие R>F, где F– табличное значение F -критерия Фишера на уровне значимости α при числе степеней свободы (n-С-2р)/2.

2. Тест ранговой корреляции Спирмена. Суть теста заключается в том, что в случае гетероскедастичности остатки ε коррелированы со значениями фактора х. Эту корреляцию можно измерить с помощью коэффициента ранговой корреляции Спирмена:

,

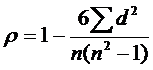где d – абсолютная разность между рангами значений х и ε.

Статистическая значимость данного коэффициента оценивается с помощью t-критерия:

Если (табличное значение t -критерия Стьюдента на уровне значимости α и при числе степеней свободы (n –2)), то корреляция между х и ε статистически значима, т.е. имеет место гетероскедастичность остатков. В противном случае принимается гипотеза об отсутствии гетероскедастичности.

3. Рассмотренные методы не дают количественной оценки зависимости дисперсии ошибок регрессии от соответствующих значений факторов. Они лишь позволяют определить наличие или отсутствие гетероскедастичности остатков. Поэтому если гетероскедастичность остатков установлена, можно количественно оценить зависимость дисперсии ошибок регрессии от значений факторов. Для этого используются тесты Уайта, Парка, Глейзера и др.

IV предпосылка МНК. Отсутствие автокорреляции остатков.

Под автокорреляцией остатков понимают зависимость распределения значений остатков друг от друга. Это означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Оценить эту зависимость можно, вычислив коэффициент корреляции между этими остатками по формуле линейного коэффициента корреляции:

Если этот коэффициент окажется существенно отличным от нуля, то остатки автокоррелированны.

V предпосылка МНК о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев Фишера и Стьюдента. Вместе с тем, оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т.е. при нарушении пятой предпосылки МНК.

При нарушении гомоскедастичности и наличии автокорреляции рекомендуется заменять традиционный МНК обобщенным методом.