Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в модель.
Частные показатели корреляции широко используются при отборе факторов, когда необходимо оценить целесообразность включения того или иного фактора в уравнение множественной регрессии. Кроме того, они позволяют ранжировать факторы по тесноте их связи с результатом.
Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
В общем виде частный коэффициент корреляции, измеряющий влияние на у фактора хi при неизменном уровне других факторов, можно определить по формуле:
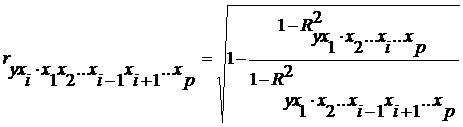 ,
,
где 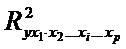 - коэффициент множественной детерминации для модели с полным набором факторов;
- коэффициент множественной детерминации для модели с полным набором факторов;
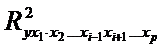 - тот же показатель, но без введения в модель фактора xi.
- тот же показатель, но без введения в модель фактора xi.
При i=1 формула примет вид:
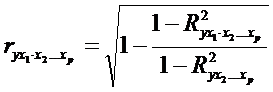
Коэффициенты частной корреляции могут быть первого, второго, третьего и т.д. порядка. Это зависит от того, влияние скольких факторов элиминируется.
Частная корреляция первого порядка – когда фиксируется теснота связи двух переменных при устранении влияния одного фактора: 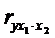 (точка отделяет фактор, значение которого элиминируется (закрепляется на неизменном уровне)).
(точка отделяет фактор, значение которого элиминируется (закрепляется на неизменном уровне)).
Частная корреляция второго и т.д. порядка – когда фиксируется теснота связи двух переменных при устранении влияния двух и более факторов, например:
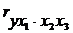 - частная корреляция второго порядка при постоянном действии факторов х2 и х3;
- частная корреляция второго порядка при постоянном действии факторов х2 и х3;
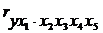 - частная корреляция четвертого порядка при постоянном действии факторов х2, х3, х4, х5.
- частная корреляция четвертого порядка при постоянном действии факторов х2, х3, х4, х5.
Соответственно, коэффициенты парной корреляции называются коэффициентами нулевого порядка.
Коэффициенты частной корреляции более высоких порядков можно найти через коэффициенты частной корреляции более низких порядков по рекуррентной формуле:
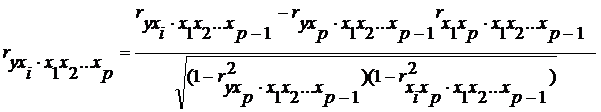
При i=1 и двух факторах формула примет вид:

При i=2 и двух факторах:
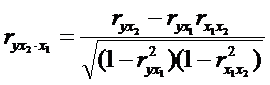
Частные коэффициенты корреляции, рассчитанные по рекуррентной формуле, изменяются в пределах от -1 до +1, а по формуле через множественный коэффициент детерминации – от 0 до 1.
Сравнение частных коэффициентов друг с другом позволяет ранжировать факторы по тесноте их связи с результатом. Обычно частные коэффициенты корреляции не имеют самостоятельного значения, они используются на стадии формирования модели, в частности в процедуре отсева факторов.
Контрольные вопросы:
1. В каких ситуациях применяется множественная регрессия?
2. Какие этапы включает в себя построение уравнения множественной регрессии?
3. Какие виды уравнений множественной регрессии различают?
4. Что означает построение модели множественной регрессии в стандартизированном масштабе?
5. Что показывают стандартизированные коэффициенты регрессии?
6. По какой формуле рассчитывается показатель множественной регрессии?
7. Что характеризуют частные коэффициенты корреляции?
Литература: [1], [2].
 2017-12-16
2017-12-16 7828
7828
