Во II группу аксиом Гильберта не входят такие понятия как пространство, полупространство, луч, полуплоскость. Об этом говорилось выше.
III группа Аксиомы конгруэнтности
Основным неопределяемым понятием в этой группе аксиом Гильберта является понятие " конгруэнтности", или " равенства", отрезков и углов. Будем использовать слово равенство и обозначения: AB = CD ( для отрезков) и 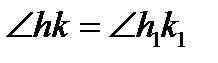 или
или 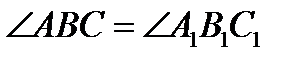 ; ( для углов).
; ( для углов).
III1 Если А и В - две точки прямой а и А' - точка на той же прямой или на другой прямой 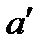 , то всегда можно найти по данную от точки А' сторону прямой а' такую точку
, то всегда можно найти по данную от точки А' сторону прямой а' такую точку 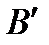 , что АВ = A
, что АВ = A 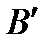 . Для каждого отрезка АВ требуется АВ = ВА. '
. Для каждого отрезка АВ требуется АВ = ВА. '
III2 Если 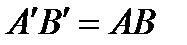 и
и 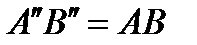 , то
, то 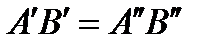 .
.
III3 Пусть АВ и BC - два отрезка прямой а, не имеющие общих внутренних точек, и пусть 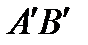 и В'С' - два отрезка на той же или другой прямой
и В'С' - два отрезка на той же или другой прямой 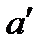 , тоже не имеющие общих точек. Если
, тоже не имеющие общих точек. Если 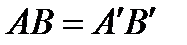 и
и 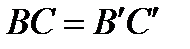 , то
, то 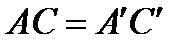 .
.
III4. Пусть в некоторой плоскости даны угол 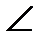 hk и луч h'. Тогда в заданной полуплоскости относительно прямой, содержащей луч
hk и луч h'. Тогда в заданной полуплоскости относительно прямой, содержащей луч 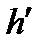 , существует и единственный луч k' такой, что
, существует и единственный луч k' такой, что 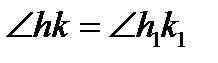 , и все внутренние точки
, и все внутренние точки 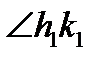 лежат в заданной полуплоскости. Каждый угол равен самому себе:
лежат в заданной полуплоскости. Каждый угол равен самому себе: 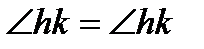
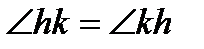 .
.
III5 Пусть А, В, С - три точки, не лежащие на одной прямой, и 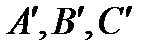 - тоже три точки, не лежащие на одной прямой. Если при этом
- тоже три точки, не лежащие на одной прямой. Если при этом 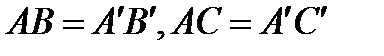 и
и 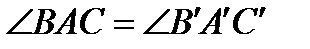 , то
, то 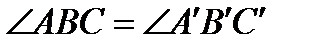 и
и 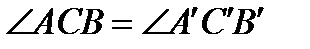 .
.
Сравним эту группу аксиом с аксиомами учебника Атанасяна.
Во-первых: Гильберт не использует такое понятие как "наложение".
 2018-01-21
2018-01-21 1294
1294
