Линейный коэффициент корреляции

При расчете этого показателя учитываются величины отклонений индивидуальных значений признака от средней, т.е. соответственно для факторного и результативного признаков величины .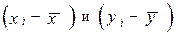

Однако непосредственно сопоставлять между собой данные абсолютные величины нельзя. Признаки могут быть выражены в разных единицах, а при одинаковых единицах измерения средние могут быть различны по величине. Сравнению подлежат отклонения, выраженные в долях среднего квадратического отклонения (нормированные отклонения).

Рассчитывают среднее произведение нормированных отклонений, которое называется линейным коэффициентом корреляции:

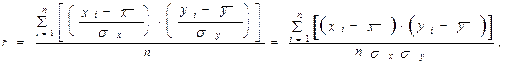
где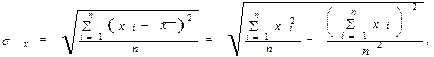

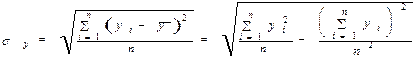
Выполнив несложные преобразования, можно получить следующую формулу для расчета линейного коэффициента корреляции:

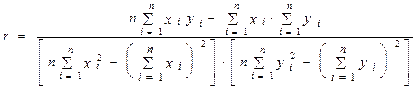
При пользовании этой формулой отпадает необходимость вычислять отклонения индивидуальных значений признаков от средней величины, что исключает ошибку в расчетах при округлении средних величин.

Линейный коэффициент корреляции может принимать любые значения в пределах от -1 до + 1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Знак при линейном коэффициенте корреляции указывает на направление связи. Прямой зависимости соответствует знак плюс, а обратной зависимости - знак минус. Линейный коэффициент корреляции применяется для измерения тесноты связи только при линейной форме связи.

Равенство 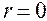говорит лишь об отсутствии линейной корреляционной зависимости, но не вообще об отсутствии корреляционной, а тем более статистической зависимости. Величина коэффициента корреляции не является доказательством наличия причинно-следственной связи между исследуемыми признаками, а является оценкой степени взаимной согласованности в изменениях признаков. Установлению причинно-следственной зависимости предшествует анализ качественной природы явлений. Особенно осторожно следует подходить к истолкованию полученных коэффициентов корреляции при незначительных объемах выборочной совокупности.

Пусть по результатам выборочного наблюдения 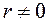. Объясняется ли это действительно существующей корреляционной связью между признаками 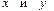в генеральной совокупности или является следствием случайности отбора элементов в выборку?

По вычисленному значению выборочного коэффициента корреляции 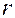требуется проверить гипотезу

Н₀: коэффициент корреляции в генеральной совокупности равен нулю при альтернативе

Н₁: коэффициент корреляции в генеральной совокупности не равен нулю.

В качестве статистического критерия для гипотезы Н₀ обычно используется величина

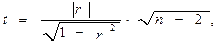
которая распределена по закону Стьюдента с 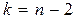степенями свободы. Гипотеза Н₀ отвергается (т.е. зависимость считается установленной), если 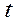превысит допустимое значение 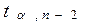при уровне значимост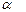и и 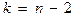степенями свободы. Некоторые значения критерия приведены ниже в таблице.

Таблица 11.

Допустимые значения критерия Стьюдента при числе степеней свободы 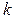и уровне значимости .

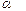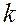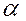0,05	0,01
	2,10	2,88
	2,09	2,86
	2,09	2,85
	2,08	2,83
	2,07	2,82
	2,07	2,81
	2,06	2,80
	2,06	2,79
	2,06	2,78
	2,05	2,77
	2,05	2,76
	2,05	2,76
	2,04	2,75
	2,02	2,70
	2,00	2,66
	1,98	2,62
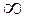	1,96	2,58

Коэффициент корреляции достаточно точно оценивает степень тесноты связи лишь в случае линейной зависимости между признаками. При криволинейной зависимости линейный коэффициент корреляции недооценивает степень тесноты связи и даже может быть равен 0, а потому в таких случаях рекомендуется использовать в качестве показателя степени тесноты связи другие величины. Рассмотрим эмпирическое корреляционное отношение .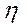

Согласно правилу сложения дисперсий, общая дисперсия 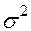равна сумме средней из групповых и межгрупповой дисперсий:

.

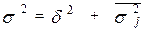Первая составляющая - межгрупповая дисперсия 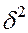, характеризует ту часть колеблемости результативного признака, которая складывается под влиянием изменения признака-фактора, положенного в основу группировки. Вариацию, обусловленную влиянием прочих факторов, характеризует средняя из  групповых дисперсий .

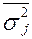Зная общую и межгрупповую дисперсии, можно оценить долю, которую составляет вариация под действием фактора 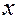в общей вариации результативного признака 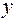, т.е. найти отношение .

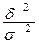Извлекая квадратный корень из этого отношения, получим эмпирическое корреляционное отношение

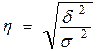или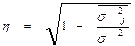

Корреляционное отношение равно нулю, когда нет колеблемости в величине средних значений результативного признака по выделенным группам. В тех случаях, когда средняя из групповых дисперсий близка к нулю, т.е. практически вся вариация результативного признака обусловлена действием фактора 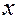, величина корреляционного отношения близка к 1. Направление связи мы легко установим по данным групповой таблицы (см. пример 9).