Линейные пространства: определение и примеры. Критерий линейной зависимости векторов

Определение линейного пространства

Пусть V - непустое множество (его элементы будем называть векторами и обозначать ...), в котором установлены правила:

1) любым двум элементам соответствует третий элемент называемый суммой элементов (внутренняя операция);

2) каждому 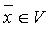и каждому отвечает определенный элемент (внешняя операция).

Множество V называется действительным линейным (векторным) пространством, если выполняются аксиомы:

I.

II.

III. (нулевой элемент, такой, что ).

IV. (элемент, противоположный элементу ), такой, что

V.

VI.

VII.

VIII.

 

Примерами линейного пространства являются:

 

1. множество столбцов

2. множество строк

3. множество ненулевых столбцов

4. множество ненулевых строк

5. все многочлены

6. многочлены степени от n до m

 

Теорема. (Необходимое и достаточное условие линейной зависимости системы векторов.)

Система векторов векторного пространства является линейно зависимой тогда и только тогда, когда один из векторов системы линейно выражается через другие вектора этой системы.

 

Базис. Примеры базисов. Координаты вектора. Свойства координатных столбцов.

Ба́зис- множество векторов в векторном пространстве, таких, что любой вектор пространства может быть единственным образом представлен в виде их линейной
СМОТРИ ЛЕКЦИИ.

 

Теорема о числе базисных векторов. Ранг системы векторов. Теорема о ранге конечной системы числовых векторов. Размерность пространства. Конечномерные и бесконечномерные пространства. Теорема о дополнении системы векторов до базиса.

Если a₁,..a_n- базис системы векторов S в пространстве V, то любой другой базис системы S также состоит из r векторов.

 r=rgS ранг системы векторов.

rg=dimV-размерность пространства

Пространство V называется конечным, если V имеет конечный базис, иначе V наз. Бесконечномерным пространством.

Например: dimE₃=3

 dimkⁿ=n

dimk[x]=∞                                                                              

Теорема: Ранг конечной системы числовых векторов(строк или столбцов) равен рангу матрицы составленной из этих векторов.

Y₁=(….) 

Y₂=(….)                                         rg=

Y_n=(….)

rg=r –размерность системы строк;

Y_i1,…Y_ir-базис системы

Теорема о дополнении системы векторов до базиса

Если размерность dimV=n; e₁, … e_n- линейно-независимая система, то e₁, … e_k расширяется до базиса пространства v.

Док-во: Если K=Y, то e₁…e_k-базис пространства v(по теореме о числе базисных векторов)

Если k<n, e₁,…e_k линейно-независимы, то существует e_k+1, не является линейной комбинацией векторов e₁…e_k.

e₁…e_k, e_k+1, e_k+2, … e_n- линейно-независима