Уравнения прямой в пространстве. Взаимное расположение прямых, прямой и плоскости

 

Прямая в пространстве в общем виде:

(1)

n1 n2

каноническое уравнение:

q (l, m, n) – направляющий вектор прямой

Прямая через 2 точки: M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂)

Параметрическое уравнение прямой в пространстве:

M₀ – решение системы уравнений(1)

q =[ n₁, n₂ ]

OM=OM₀+t q – векторная запись параметрического уравнения

Взаимное расположение прямых в пространстве:

Возможны четыре различных случая расположения двух прямых в пространстве:

 

– прямые скрещивающиеся, т.е. не лежат в одной плоскости;

– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;

– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;

– прямые совпадают.

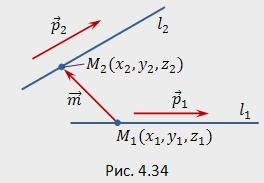
Получим признаки этих случаев взаимного расположения прямых, заданных каноническими уравнениями

 

 

где — точки, принадлежащие прямым и соответственно, a — направляющие векторы (рис.4.34). Обозначим через вектор, соединяющий заданные точки.

Перечисленным выше случаям взаимного расположения прямых и соответствуют следующие признаки:

 

– прямые и скрещивающиеся векторы не компланарны;

 

– прямые и пересекаются векторы компланарны, а векторы не коллинеарны;

 

– прямые и параллельные векторы коллинеарны, а векторы не коллинеарны;

 

– прямые и совпадают векторы коллинеарны.

 

Эти условия можно записать, используя свойства смешанного и векторного произведений. Напомним, что смешанное произведение векторов в правой прямоугольной системе координат находится по формуле:

 

Равенство нулю смешанного произведения векторов является необходимым и достаточным условием их компланарности. Поэтому:

 

– прямые и скрещивающиеся определитель отличен от нуля;

…………………………………………………………………………………………………………………………………………………………..

Теорема. Пусть плоскость задана общим уравнением

,

а прямая L задана каноническими уравнениями

или параметрическими уравнениями

, ,

в которых – координаты нормального вектора плоскости , – координаты произвольной фиксированной точки прямой L, –

координаты направляющего вектора прямой L. Тогда:

1) если , то прямая L пересекает плоскость в точке,координаты которой можно найти из системы уравнений

; (7)

2) если и , то прямая лежит на плоскости;

3) если и , то прямая параллельна плоскости.