Содержание
| Предисловие ………………………………………. | 4 |
| Цели и задачи курса ………………………………. | 5 |
| Содержание основных тем программы …………. | 5 |
| Парная регрессия …………………………………. | 6 |
| Множественная регрессия ………………………... | 18 |
| Реализация типовых задач на персональном компьютере ………………………………………... | 23 |
| Рекомендуемая литература ………………………. | 25 |
| Приложение 1 ……………………………………... | 26 |
| Приложение 2 ……………………………………... | 27 |
| Приложение 3 ……………………………………... | 28 |
| Приложение 4 ……………………………………... | 29 |
| Контрольные вопросы для проверки знаний студентов ………………………………………….. | 30 |
| Контрольная работа по дисциплине «Эконометрика» ………………………………….. | 30 |
Основные положения оценки качества знаний сту-
дентов 33
Предисловие
Успешное овладение дисциплиной “эконометрика” предполагает знание основных положений теории вероятностей и математической статистики, линейной алгебры и математического анализа, общей теории статистики, макро- и микроэкономики. Данная дисциплина иллюстрирует эффективность применения математики в задачах экономики.
Целью настоящего пособия является помощь студентам вечерней и заочной форм обучения в освоении основных положений курса. Изложение материала проводится на основе разбора типовых задач.
Экономист в своей практической деятельности использует пакеты прикладных программ, современную экономическую литературу. В связи с этим в настоящем пособии приводятся англоязычные аналоги основных показателей.
В ходе решения задачи студент должен выбрать приемлемую модель, наилучшим способом отражающую реальные процессы и произвести прогноз на заданный интервал. Такая последовательность соответствует схеме работы экономиста – “анализ-прогноз-план”.
Сложность усвоения курса вызвана также отсутствием литературы, учитывающей реальные учебные планы для студентов экономических специальностей. Автор рекомендует использовать учебники из списка, приведенного в конце методического пособия.
Цель и задачи курса
Целью дисциплины “Эконометрика” является овладение студентами методами количественного исследования экономических процессов для построения качественных эконометрических моделей и прогнозирования.
Задачами курса являются:
- обучение теории и практике формализации задач, возникающих в микро- и макроэкономике;
- развитие навыков математического моделирования экономических процессов;
- рассмотрение широкого круга задач, возникающих при анализе и прогнозировании.
В результате изучения дисциплины студент должен:
- знать области применения и содержательную сторону эконометрических моделей;
- владеть математическими методами построения и анализа основных моделей;
- уметь использовать полученные знания для прогнозирования реальных экономических процессов;
- применять информационные технологии в процессе моделирования и оптимизации.
По завершении курса студент должен выполнить контрольную работу и сдать её на рецензию в установленный срок.
Содержание основных тем программы
1. Предпосылки корреляционного и регрессионного анализов. Виды связей и характер данных в экономике.
2. Модель парной регрессии. Условия Гаусса-Маркова. Проверка значимости параметров модели и уравнения в целом.
3. Модель множественной регрессии. Условия Гаусса-Маркова. Проверка значимости параметров модели и уравнения в целом.
4. Временные ряды. Учет автокорреляции и гетероскедастичности.
5. Выявление адекватности и точности оцененных моделей. Прогнозирование.
6. Системы регрессионных уравнений.
7. Обобщенный метод наименьших квадратов.
Таблица соответствия основных параметров
| Англоязычное обозначение | Отечественное обозначение | Пояснение |
| 1. Е (х) | M(x) | Математическое ожидание |
| 2. V(x), Var(x) | D(x) = s2(x) | Дисперсия |
| 3. pop.var(x) | s2(x) | Дисперсия генеральной совокупности |
| 4. plim | - | Предел по вероятности |
| 5. cov(x, y) | K(x, y) | Ковариация |
| 6. TSS (total squares sum) | Q | Общая сумма квадратов |
| 7. ESS (error squares sum) | Qe | Сумма квадратов ошибки |
| 8. RSS (regression squares sum) | QR | Регрессионная сумма квадратов |
| 9. BLUE (Best linear unbiased estimator) | Наилучшая (с минимальной дисперсией) оценка в классе несмещенных линейных оценок | |
| 10. Стандартное отклонение, S | 1.Исправленное среднеквадратическое отклонение. 2. Выборочное среднеквадратическое отклонение | |
| 11. F.O.C. (first order condition) | Необходимое условие экстремума | |
| 12. S.O.C. (second order condition) | Достаточное условие экстремума | |
| 1 13. df (degrees of freedom) | ||
| 14. MSS (mean squares sum) | Сумма квадратов, деленная на число степеней свободы Оценка дисперсии.
| |
| 15. P-value | Р-значение, Р( | |
Парная регрессия
Рассмотрим типовую задачу. Пусть имеются данные о стоимости произведенной продукции (О) и стоимости основных производственных фондов (Ф) за год.
| t(мес) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| О | 48 | 50 | 52 | 58 | 57 | 60 | 62 | 68 | 70 | 71 | ||
| Ф | 24 | 26 | 30 | 32 | 35 | 40 | 42 | 45 | 46 | 48 | 51 | 53 |
1. Исходя из экономических соображений, определяем, что факторным признаком (х) является стоимость основных производственных фондов (Ф), а результативным (у) – объем произведенной продукции (О).
В данной задаче имеем два вида данных: перекрестный и временной ряд (у (х), у(t)).
Данные получены путем случайной выборки из достаточно большой генеральной совокупности. Следовательно, закономерности в изменении фактических данных есть лишь отражение общих закономерностей в генеральной совокупности.
2. Проведем графический анализ фактических данных для модели парной регрессии и модели временного ряда. Для этого на соответствующих диаграммах рассеяния отразим фактическое изменение объема произведенной продукции (у) от стоимости фондов (х) и изменение у от t.
Для двух истинных моделей:

определяем ориентировочный вид зависимости:

Характер зависимостей может быть оценен также исходя из экономических соображений, а также на основании специальных процедур.
3. Допустим, выбраны линейные модели:
 и
и

Данные модели мы будем называть истинными, как отражающими закономерности в генеральной совокупности. Выбор типа модели, а также регрессоров, входящих в модель, называется спецификацией. Само уравнение регрессии описывает “процесс, порождающий данные”.
Причина появления ошибки (возмущения) e состоит в неполном учете всех параметров, неточности измерений.
Модель называется нормальной линейной регрессионной, если выполнены условия Гаусса-Маркова:
1. Зависимая величина у (или возмущение e) есть величина случайная, а объясняющая переменная х – величина неслучайная.
2. М(e) = 0
3. D(e) = s2 = const
4. Cov(ei; ej) = 
5. Зависимая величина у (или возмущение e) есть нормально распределенная случайная величина.
Студентам следует обратить особое внимание на осмысление условий Гаусса-Маркова.
Первое условие характеризует выбранный тип связи.
Второе условие говорит о том, что ошибка в среднем равна нулю (иначе это не ошибка, а неучтенный фактор).
Третье условие характеризует режим гомоскедастичности, в противном случае – гетероскедастичности. Дисперсия случайного члена должна оставаться постоянной.
Четвертое условие предполагает отсутствие систематической связи между значениями случайного члена (отсутствие автокорреляции).
Пятое условие не является обязательным, его соблюдение дает возможность проводить интервальную оценку.
В реальных условиях могут существовать процессы, не вписывающиеся в модель (например, корректировка планов, и т.д.). Однако, все явления, не учтенные при спецификации, будут для нас источниками ошибок, т.е. будут вредными.
Реальная экономика – это очень сложная, многофакторная, открытая система. Измерить параметры истинной модели не представляется возможным. Поэтому произведем оценку параметров генеральной совокупности (на примере модели парной регрессии).
 - истинная модель
- истинная модель

 - оцененная модель, где
- оцененная модель, где
a0 =  0 - оценка a0,
0 - оценка a0, 
a1 =  1 - оценка a1,
1 - оценка a1,
е = 
 - оценка e; e = y -
- оценка e; e = y - 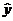 .
.
Подобрать а0 и а1 это значит обеспечить наилучшую точность приближения оцененной модели к истинной. Ошибка е - это различие между фактическими и расчетными данными. 
Оценки параметров регрессии получают исходя из следующего условия:



Другие возможные формы представления:
 ;
;  .
.
Удобно для вычислений использовать уравнение в отклонениях:
 .
.
Согласно теореме Гаусса-Маркова МНК-оценки не только обеспечивают наилучшую точность, но и являются наилучшими оценками в классе несмещенных оценок (BLUE). При этом дисперсия ошибок  , а дисперсия оценок:
, а дисперсия оценок:


Для определения МНК-оценок составим таблицу.
| у | х |  |  |  |  |  | 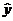  |  |  |  |
| 48 | 24 | -11,6 | -12.8 | 148,5 | 163,8 | 134,6 | 47,7 | 0,3 | 0,1 | 576 |
| 50 | 26 | -9,6 | -10.8 | 103,7 | 116,6 | 92,2 | 49,6 | 0,4 | 0,2 | 676 |
| 52 | 30 | -7,6 | -6.8 | 51,7 | 46,2 | 57,8 | 53,3 | -1,3 | 1,7 | 900 |
| 58 | 32 | -1,6 | -4.8 | 7,7 | 23,0 | 2,6 | 55,2 | 2,8 | 8,1 | 1024 |
| 57 | 35 | -2,6 | -1,8 | 4,7 | 3,2 | 6,8 | 58,0 | -1,0 | 1,0 | 1225 |
| 60 | 40 | 0,4 | 3,2 | 1,3 | 10,2 | 0,2 | 62,6 | -2,6 | 6,8 | 1600 |
| 62 | 42 | 2,4 | 5,2 | 12,5 | 27,0 | 5,8 | 64,5 | -2,5 | 6,1 | 1764 |
| 68 | 45 | 8,4 | 8,2 | 68,9 | 67,2 | 70,6 | 67,3 | 0,8 | 0,6 | 2025 |
| 70 | 46 | 10,4 | 9,2 | 95,7 | 84,6 | 108,2 | 68,2 | 1,8 | 3,3 | 2116 |
| 71 | 48 | 11,4 | 11,2 | 127,7 | 125,4 | 130,0 | 70,0 | 1,.0 | 1,0 | 2304 |
| 596 | 368 | 0 | 0 | 622,2 | 667,6 | 608,4 | -0,3 | 28,5 | 14210 |
Здесь  = 36,8,
= 36,8,  = 59,6.
= 59,6.
Итоговые данные таблицы позволяют определить МНК-оценки параметров линейной парной регрессии: а0 = 25,4; а1 = 0,93. Таким образом, оцененная модель имеет вид:  .
.
Полезно определить выборочную оценку коэффициента корреляции:

Для правильно специфицированной модели связь между зависимой (у) и независимой (х) переменными должна быть сильной.
По принятой классификации 
В нашем случае r = 0,98 – сильная положительная связь.
Качество оцененной модели характеризует коэффициент детерминации R2:


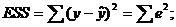

Для нашего случая 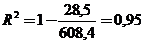 .
.
Это значит, что изменение зависимой переменной y на 95 % объясняется моделью и на 5 % прочими факторами.
Проверить значимость уравнения в целом и отдельных параметров модели можно, используя соответствующие нулевые гипотезы.
В общем случае для уравнения множественной регрессии
у = a0 + a1х + a2х + …anхn + e
Н0: a1 = a2 = … = an = 0.
Сравнивают наблюдаемое и критическое значения критерия Фишера-Снедекора. Гипотеза выполняется, если Fнабл < Fкр.
 (для парной регрессии).
(для парной регрессии).
Fкр находят по соответствующим таблицам, исходя из принятой доверительной вероятности. В нашем случае Fкр(0,95; 1; 8) = 5,32.

Так как Fнабл > Fкр нулевую гипотезу отвергаем. Уравнение в целом значимо.
Значимость параметров модели оцениваем исходя из гипотез:
Н0: a0 = 0; Н0: a1 = 0.
Н1: a0  0; Н1: a1
0; Н1: a1  0.
0.
Гипотеза принимается, если tнабл < tкр.


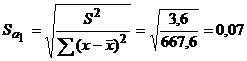
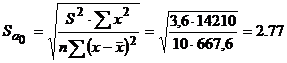
Для удобства в эконометрике принята следующая форма записи оцененной модели:

 R2 = 0, 98
R2 = 0, 98
(2,77) (0,07)

tкр для a = 5% и количестве степеней свободы к = n – 2 = 8 находим по таблицам распределения Стьюдента. tкр (0,95; 8) = 2,3.
 , следовательно, нулевые гипотезы отвергаем.
, следовательно, нулевые гипотезы отвергаем.
Полезно проверить гипотезу о значимости коэффициента корреляции: Н0:r =0; Н1:r  0;
0;
 аналогично сравниваем с tкр.
аналогично сравниваем с tкр.
Важнейшим этапом является интерпретация полученных результатов. Для оцененной модели  - увеличение стоимости основных производственных фондов на 1 единицу ведет к росту объема продукции на 0,93 единиц. При отсутствии производственных фондов объем продукции равен 25,4 единиц. Интерпретация параметра а0 может и не иметь экономического смысла.
- увеличение стоимости основных производственных фондов на 1 единицу ведет к росту объема продукции на 0,93 единиц. При отсутствии производственных фондов объем продукции равен 25,4 единиц. Интерпретация параметра а0 может и не иметь экономического смысла.
Графический анализ временного ряда показывает отсутствие сезонной компоненты. Следовательно, модель  представляет собой линейный временной тренд. Построение и анализ оцененной модели тренда аналогичен вычислениям, произведенным для парной регрессии - проводим простую замену одной независимой переменной х на другую – t.
представляет собой линейный временной тренд. Построение и анализ оцененной модели тренда аналогичен вычислениям, произведенным для парной регрессии - проводим простую замену одной независимой переменной х на другую – t.
Важной разновидностью модели временного ряда являются адаптивные модели. В процедуре нахождения сглаженного уровня используют значения только предшествующих уровней ряда, взятые с определенным весом, причем вес наблюдения уменьшается по мере удаления его от момента сглаживания. Обозначим сглаженные значения как St, тогда
 где
где
a - параметр сглаживания,
b = 1 - a - параметр дисконтирования.
По модели Брауна:
ур(t) = а0(t - 1) + a1(t - 1)k, где
k – шаг прогнозирования. Примем k = 1.
ур(t) = а0(t - 1) + a1(t - 1)
а0(t) = a1(t - 1) + а0(t - 1) +e(t)(1 - b2)
a1 (t) = a1 (t - 1) + e (t) a2
Примем a = 0,4; b = 0,6. Тогда модель Брауна примет следующий вид:
ур(t) = а0(t - 1) + a1(t - 1);
а0(t) = a1(t - 1) + а0(t - 1) + 0,64 е(t);
a1 (t) = a1 (t - 1) + 0, 16 e (t)
Таким образом, на каждом шаге в зависимости от величины ошибки происходит корректировка параметров, модель адаптируется к изменяющимся условиям.
Для выявления начальных значений параметров а0 и а1 анализируют первые пять точек временного ряда.
Составим расчетную таблицу
| t | y | 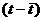 |  |  |  |
| 1 | 48 | -2 | -5 | 10 | 4 |
| 2 | 50 | -1 | -3 | 3 | 1 |
| 3 | 52 | 0 | -1 | 0 | 0 |
| 4 | 58 | 1 | 5 | 5 | 1 |
| 5 | 57 | 2 | 4 | 8 | 4 |
| 15 | 265 | 0 | 0 | 26 | 10 |

 ;
;



Процесс продолжается до t = 10. Полученное на последнем шаге уравнение является основой для линейной экстраполяции тренда. Отметим, что корректировка параметров а0 и а1 геометрически означает вращение в плоскости прямой, её “адаптацию” на изменение ошибки метода.
Таким образом, нами получены оценочные модели парной регрессии, временного тренда и модели Брауна. Для прогнозирования возможно использование только качественных моделей. Модель признается качественной, если она адекватна и точна. Адекватность модели означает её соответствие условиям Гаусса-Маркова. Поскольку прямое определение ошибки истинной модели невозможно, то исследуются ошибки оцененной модели. Адекватность устанавливается в виде проверки соответствующих гипотез.
Составим расчетную таблицу.
| y | e | Т П. | (e(t) – e(t-1))2 | e(t) × e(t-1) |  |
| 48 | 0,3 | - | - | - | 0,6 |
| 50 | 0,4 | 1 | 0,01 | 0,12 | 0,8 |
| 52 | -1,3 | 1 | 2,89 | -0,52 | 2,5 |
| 58 | 2,8 | 1 | 16,81 | -3,6 | 4,8 |
| 57 | -1,0 | 0 | 14,44 | -2,8 | 1,8 |
| 60 | -2,6 | 1 | 2,56 | 2,6 | 4,3 |
| 62 | -2,5 | 0 | 0,01 | 6,5 | 4,0 |
| 68 | 0,8 | 0 | 10,89 | -2,0 | 1,2 |
| 70 | 1,8 | 1 | 1,0 | 1,44 | 2,6 |
| 71 | 1,0 | - | 0.64 | 1,8 | 1,4 |
| å 59,6 | -0,3 | 5 | å 49,99 | 3,5 | 2,4 |
1. Проверка гипотезы о равенстве нулю математического ожидания ошибки.
Используется t-критерий, описанный ранее.
 .
. 
Гипотеза принимается, если tнаб < tкр.
В нашем случае  . tкр = 2,3. Гипотеза принимается.
. tкр = 2,3. Гипотеза принимается.
2. Проверка случайности ряда остатков на основе критерия поворотных точек. Точка в ряду ошибок признается поворотной (т.п.), если она больше или меньше последующей и предыдущей. Сумма поворотных точек для n = 10 и a = 5% должна быть больше критического значения -

В нашем случае 5 > 2. Критерий адекватности выполнен.
3. Проверка отсутствия автокорреляции на основе критерия Дарбина-Уотсона.
 .
.
В специальных таблицах табулированы значения d1 и d2; в нашем случае d1 = 1,08, d2 = 1,36;  .
.
Если dнабл Î (0; d1) –уровни сильно автокоррелированы, модель неадекватна. При dнабл Î (d2; 2) – уровни независимы. Если dнабл Î (d1; d2), требуются дополнительные исследования значимости коэффициента автокорреляции.
 ,
,
В нашем случае r (1) = 0,07 –связь практически отсутствует.
Значимость можно определить либо по t-критерию, либо по таблице Фишера-Йейтса. Так  , следовательно, коэффициент автокорреляции не значим.
, следовательно, коэффициент автокорреляции не значим.
Если dнабл > 2, то исследуют  .
.
4. Проверка гипотезы о нормальном законе распределения ряда остатков. Наиболее прост RS-критерий.
 .
.
Наблюдаемое значение RS должно попадать в интервал от 2,7 до 3,7. В нашем случае RS= 3,.03. Гипотеза принимается.
Для характеристики точности используется средняя относительная ошибка:

Если ошибка менее 5%, то точность признается высокой; если менее 15%, то допустимой.
Точечный прогноз на k шагов вперед при экстраполяции линейного тренда достигается подстановкой t = 10 и t = 11. В модели парной регрессии подставляем х10 и х11. В модели Брауна подставляем k=1 и k=2.
Доверительный интервал прогнозов будет иметь следующие границы:
Верхняя граница прогноза = yр(n + k) + 
Нижняя граница прогноза = yр(n + k) - 
 - для временного ряда и модели Брауна
- для временного ряда и модели Брауна
При вычислении ошибки прогноза для модели Брауна используется значение подкоренного выражения модели временного ряда.
 - для парной регрессии.
- для парной регрессии.
 - стандартное отклонение ошибки
- стандартное отклонение ошибки
Для временного ряда и модели Брауна значения табулированы .
Для парной регрессии хn+k = x11; x12.
Образец оформления прогноза.
| х | Шаг, k | Прогноз, yр(t) | Нижняя граница | Верхняя граница |
| 51 | 1 | 72,83 | 67,7 | 77,96 |
| 52 | 2 | 74,69 | 69,39 | 79,99 |
Прогноз оформляется для всех трех использованных моделей. В заключении приводится итоговая сравнительная таблица
| Модель |  отн отн | Se |
| 1. Парная линейная регрессия | 2,4 | 1,89 |
| 2. Временной тренд | 1,85 | 1,43 |
| 3. Адаптивная модель Брауна | 3,.41 | 2,78 |
На основании сравнительного анализа полученных результатов студент должен выдать рекомендации по использованию моделей прогнозирования.
Множественная регрессия
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Рассматривается два круга вопросов: отбор факторов и выбор вида уравнения регрессии. Факторы должны быть количественно измеримы и не дублировать друг друга. Студент должен уметь составлять и анализировать матрицу парных коэффициентов корреляции. Наиболее проста в интерпретации и доступна для вычислений модель множественной линейной регрессии.
Условия Гаусса – Маркова имеют следующий вид:
1. yt = a1 xt1 + a2 xt2 +…+ akxtk + et;
t = 1… n – спецификация модели.
2. xt1… xtk – детерминированные величины.
3.  - не зависят от t.
- не зависят от t.
4. 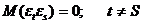 .
.
5.  ~ N(0,s2).
~ N(0,s2).
Удобна запись в матричном виде.

Тогда для нормальной линейной регрессионной модели:
1. Y = X a + e
2. X – детерминированная матрица с максимальным рангом k.
3. М(e) = 0; М (e eт) = s2 En - матрица ковариаций.
4. e ~ N (0, s2 En)
Выборочной оценкой этой модели является уравнение:
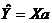 , где
, где

Для определения МНК-оценок используем условие:

Решением является вектор а = (ХТХ)-1 XТ Y

 .
.
Вариации оценок параметров определяют точность уравнения множественной регрессии.
Выборочная оценка ковариационной матрицы
Cov (a) = S2 (XT X)-1, где
S2 – выборочная остаточная дисперсия,
 .
.
Оценка дисперсии коэффициента регрессии  является диагональным элементом матрицы cov(a). Значимость аi определяется по t-критерию путем сравнения с tкр (1-a; n-k-1).
является диагональным элементом матрицы cov(a). Значимость аi определяется по t-критерию путем сравнения с tкр (1-a; n-k-1).
Значимость уравнения в целом проверяется исходя из F-критерия.

Если модель адекватна и точна, то возможен прогноз.
y (n+k) = yp(k) ± u(k), где

Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости. Для устранения таких различий применяют средние частные коэффициенты эластичности

и  - коэффициенты:
- коэффициенты:  .
. 
Коэффициент эластичности показывает, на сколько процентов изменится зависимая переменная при изменении фактора j на 1%. Бета-коэффициент показывает, на какую часть величины среднего квадратического отклонения  y изменится зависимая переменная Y с изменением Х на величину своего среднеквадратического отклонения при фиксированном на постоянном уровне значения остальных независимых переменных.
y изменится зависимая переменная Y с изменением Х на величину своего среднеквадратического отклонения при фиксированном на постоянном уровне значения остальных независимых переменных.
Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта-коэффициентов:
 где
где
r (j) – коэффициент парной корреляции между фактором и зависимой переменной.
Рассмотрим известный пример:
Бюджетное обследование пяти случайно выбранных семей дало следующие результаты:
| Семья | Накопление, S | Доход, Y | Имущество, W |
| 1 | 3 | 40 | 60 |
| 2 | 6 | 55 | 36 |
| 3 | 5 | 45 | 36 |
| 4 | 3,5 | 30 | 15 |
| 5 | 1,5 | 30 | 90 |
Истинная модель: S = a0 + a1Y + a2W + e
Оцененная модель:  = X a
= X a
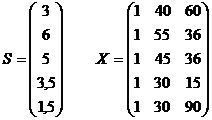
Вычислим:

Отметим, что обратную матрицу удобно находить, используя преобразования Жордана-Гаусса.
В итоге
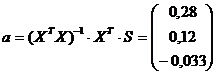 ,
,
Оцененная модель:
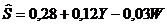
Интерпретация модели:
- изменение дохода на 1 единицу приведет к увеличению накопления на 0,12 единиц;
- увеличение стоимости имущества на 1 единицу приведет к уменьшению накопления на 0,03 денежных единиц.
ESS = (S-  (S-
(S- 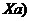 = 0,281, df1 = 2.
= 0,281, df1 = 2.
RSS = ( -
-  = 12,019, df 2= 2.
= 12,019, df 2= 2.
 - 97% изменения накопления объясняются моделью, 3% - неучтенными факторами.
- 97% изменения накопления объясняются моделью, 3% - неучтенными факторами.
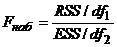 = 42,75
= 42,75
Fкр (0, 05; 2; 2) = 19; Fнаб >Fкр, уравнение признается значимым в целом.
 ,
,
Cov (a) = S2 × (XT X)-1;
 0, 80
0, 80 





Отметим, что несмотря на то, что а0 незначим (tH < tкр), уравнение, исходя из F-критерия в целом значимо.
Пусть некоторая семья имеет доход Y = 30 и имущество W = 52,5.
Определим прогнозное значение накоплений. Для шестой семьи  .
.



В предположении, что для шестой семьи выявленная тенденция сохранится, 95%-й доверительный интервал будет иметь следующий вид:


Верхняя граница прогноза - 8,83 усл. ден.ед.
Нижняя граница прогноза – 3,93 усл. ден.ед.

Составим вспомогательную таблицу:
 |  |  | 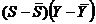 |  |
| -0,8 | 0 | 12,6 | 0 | -10,08 |
| 2,2 | 15 | -11,4 | 33 | -25,08 |
| 1,2 | 5 | -11,4 | 6 | -13,68 |
| -0,3 | -10 | -32,4 | 3 | 9,72 |
| -2,3 | -10 | 42,6 | 23 | -98,00 |
| Итого | 0 | 0 | 65 | -137,12 |

 ;
;

 2018-02-14
2018-02-14 1351
1351

 .
.