Пример 1. По территориям региона приводятся данные за 199X г.
(таб. 1.1).
Таблица 1.1
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., x | Среднедневная заработная плата, руб., y |
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задания:
1. Рассчитать линейный коэффициент парной корреляции, оценить его статистическую значимость и построить для него доверительный интервал с уровнем значимости a=0,05.
2. Построить линейное уравнение парной регрессии y на x и оценить статистическую значимость параметров регрессии. Сделать рисунок.
3. Оценить качество уравнения регрессии при помощи коэффициента детерминации. Проверить качество уравнения регрессии при помощи F -критерия Фишера.
4. Выполнить прогноз заработной платы y при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал для уровня значимости a=0,05.
Решение
1. Для определения степени тесноты связи обычно используют линейный коэффициент корреляции:
 ,
,
где  ,
,  – выборочные дисперсии переменных x и y,
– выборочные дисперсии переменных x и y,  – ковариация признаков. Соответствующие средние определяются по формулам:
– ковариация признаков. Соответствующие средние определяются по формулам:
 , , |  , , |
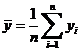 , , |  . . |
Для расчета коэффициента корреляции (1.1) строим расчетную таблицу (табл. 1.2):
Таблица 1.2
| x | y | xy | x2 | y2 |  |  | e2 | |
| 1 | 78 | 133 | 10374 | 6084 | 17689 | 148,77 | -15,77 | 248,70 |
| 2 | 82 | 148 | 12136 | 6724 | 21904 | 152,45 | -4,45 | 19,82 |
| 3 | 87 | 134 | 11658 | 7569 | 17956 | 157,05 | -23,05 | 531,48 |
| 4 | 79 | 154 | 12166 | 6241 | 23716 | 149,69 | 4,31 | 18,57 |
| 5 | 89 | 162 | 14418 | 7921 | 26244 | 158,89 | 3,11 | 9,64 |
| 6 | 106 | 195 | 20670 | 11236 | 38025 | 174,54 | 20,46 | 418,52 |
| 7 | 67 | 139 | 9313 | 4489 | 19321 | 138,65 | 0,35 | 0,13 |
| 8 | 88 | 158 | 13904 | 7744 | 24964 | 157,97 | 0,03 | 0,00 |
| 9 | 73 | 152 | 11096 | 5329 | 23104 | 144,17 | 7,83 | 61,34 |
| 10 | 87 | 162 | 14094 | 7569 | 26244 | 157,05 | 4,95 | 24,46 |
| 11 | 76 | 159 | 12084 | 5776 | 25281 | 146,93 | 12,07 | 145,70 |
| 12 | 115 | 173 | 19895 | 13225 | 29929 | 182,83 | -9,83 | 96,55 |
| Итого | 1027 | 1869 | 161808 | 89907 | 294377 | 0 | 1574,92 | |
| Среднее значение | 85,58 | 155,75 | 13484,00 | 7492,25 | 24531,42 |
По данным таблицы находим:
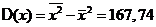 ,
,  ,
,
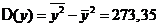 ,
,  ,
,
 ,
,  ,
,
 ,
, 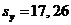 ,
,
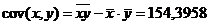 ,.
,.  .
.
Таким образом, между заработной платой (y) и среднедушевым прожиточным минимумом (x) существует прямая достаточно сильная корреляционная зависимость.
Для оценки статистической значимости коэффициента корреляции рассчитывают двухсторонний t-критерий Стьюдента:
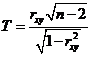 ,
,
который имеет распределение Стьюдента с k = n –2 и уровнем значимости a.
В нашем случае
 и
и  .
.
Поскольку  , то коэффициент корреляции существенно отличается от нуля.
, то коэффициент корреляции существенно отличается от нуля.
Для значимого коэффициента можно построить доверительный интервал, который с заданной вероятностью содержит неизвестный генеральный коэффициент корреляции. Для построения интервальной оценки (для малых выборок n <30), используют z-преобразование Фишера:

Распределение z уже при небольших n является приближенным нормальным распределением с математическим ожиданием  и дисперсией
и дисперсией 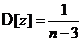 . Поэтому вначале строят доверительный интервал для M[ z ], а затем делают обратное
. Поэтому вначале строят доверительный интервал для M[ z ], а затем делают обратное
z -преобразование.
Применяя z -преобразование для найденного коэффициента корреляции, получим
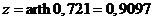 .
.
Доверительный интервал для M(z) будет иметь вид
 ,
,
где t g находится с помощью функции Лапласа F(t g)=g/2. Для g=0,95 имеем t g=1,96. Тогда
 ,
,
или
 .
.
Обратное z -преобразование осуществляется по формуле
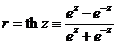
В результате находим
 .
.
В указанных границах на уровне значимости 0,05 (с надежностью 0,95) заключен генеральный коэффициент корреляции r.
2. Таким образом, между переменными x и y имеет существенная корреляционная зависимость. Будем считать, что эта зависимость является линейной. Модель парной линейной регрессии имеет вид
 ,
,
где y – зависимая переменная (результативный признак), x – независимая (объясняющая) переменная, e – случайные отклонения, b0 и b1 – параметры регрессии. По выборке ограниченного объема можно построить эмпирическое уравнение регрессии:
 ,
,
где b 0 и b 1 – эмпирические коэффициенты регрессии. Для оценки параметров регрессии обычно используют метод наименьших квадратов (МНК). В соответствие с МНК, сумма квадратов отклонений фактических значений зависимой переменной y от теоретических  была минимальной:
была минимальной:
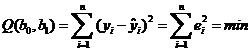 ,
,
где  – отклонения yi от оцененной линии регрессии. Необходимым условием существования минимума функции двух переменных (1.12) является равенство нулю ее частных производных по неизвестным параметрам b0 и b1. В результате получаем систему нормальных уравнений:
– отклонения yi от оцененной линии регрессии. Необходимым условием существования минимума функции двух переменных (1.12) является равенство нулю ее частных производных по неизвестным параметрам b0 и b1. В результате получаем систему нормальных уравнений:

Решая систему (1.13), найдем
 ,
,
 .
.
По данным таблицы (1.2) находим
 ;
;
 .
.
Получено уравнение регрессии:
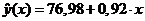 .
.
Параметр b 1 называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. В рассматриваемом случае, с увеличением среднедушевого минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.

Рис. 1.1
Отметим, что уравнение регрессии (1.16) можно получить матричным способом, что особенно удобно при компьютерном моделировании подобных процессов. Введем следующие матрицы
 ,
,  ,
,  .
.
Тогда коэффициенты множественной регрессии можно найти следующим образом:
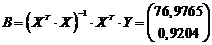 .
.
Здесь матрицы перемножались с пользованием программы MathCAD.
Проверка адекватности моделей, построенных на основе уравнений регрессии, начинается с проверки статистической значимости каждого коэффициента регрессии. Для этого вычислим сначала стандартную ошибку регрессии
 . (1.17)
. (1.17)
В нашем случае
 .
.
Значимость коэффициентов регрессии осуществляется с помощью t-критерия Стьюдента:
 , (1.18)
, (1.18)
где  – стандартная ошибка коэффициента регрессии.
– стандартная ошибка коэффициента регрессии.
Для коэффициента b 1 оценку дисперсии можно получить по формуле:
 . (1.19)
. (1.19)
В нашем случае

Следовательно,
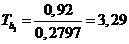 .
.
Отметим, что для парной линейной регрессии t -критерий для коэффициента корреляции rxy и коэффициента регрессии b 1 совпадают.
Для коэффициента b 0 оценку дисперсии можно получить по формуле:
 . (1.20)
. (1.20)
Тогда
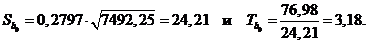
Критическое значение критерия было уже найдено  . Поскольку
. Поскольку  и
и  , то коэффициенты регрессии значимо отличаются от нуля. Следовательно, для них можно построить доверительные интервалы.
, то коэффициенты регрессии значимо отличаются от нуля. Следовательно, для них можно построить доверительные интервалы.
Отметим, что оценки (1.19) и (1.20) также можно получить матричным способом:
 ,
,
где  . Отсюда получаем, что
. Отсюда получаем, что  и
и  .
.
Определим предельные ошибки для каждого показателя:
 ,
, 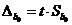 ,
,
где  . В нашем случае
. В нашем случае
 ,
, 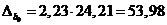 .
.
В результате, получаем следующие доверительные интервалы для коэффициентов регрессии:
 и
и 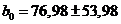 ,
,
или
 и
и  .
.
Замечание. Задачи регрессионного анализа можно решать с использованием компьютеров. Например, можно использовать программу Excel. Для этого достаточно ввести свои данные и использовать пакет Анализ данных. Опишем кратко последовательность действий:
1) Проверьте доступ к пакету анализа. В главном меню последовательно выберите Сервис / Надстройки. Установите флажок Пакет анализа.
2) В главном меню выберите Сервис / Анализ данных / Регрессия. Щелкните по кнопке ОК.
3) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон столбцов, содержащие значения факторов независимых признаков.
Результаты регрессионного анализа представлены в таблице 1.3.
Отметим, что в компьютерных программах вычисляется не критическое значение критерия, допустим Tкрит, а вероятность  . Если P <a, то нет оснований отклонять нулевую гипотезу, если P >a, то нулевая гипотеза отклоняется.
. Если P <a, то нет оснований отклонять нулевую гипотезу, если P >a, то нулевая гипотеза отклоняется.
Таблица 1.3
| ВЫВОД ИТОГОВ |
|
|
|
|
|
| |
| Регрессионная статистика |
|
|
|
|
| ||
| Множественный R | 0,721025214 |
|
|
|
| ||
| R-квадрат | 0,519877359 |
|
|
|
|
| |
| Нормированный | 0,471865095 |
|
|
|
|
| |
| Стандартная ошибка | 12,5495908 |
|
|
|
|
| |
| Наблюдения | 12 |
|
|
|
|
| |
|
|
|
|
|
| |||
| df | SS | MS | F | Значимость F |
| ||
| Регрессия | 1 | 1705,327706 | 1705,327706 | 10,82801173 | 0,008141843 |
| |
| Остаток | 10 | 1574,922294 | 157,4922294 |
|
|
| |
| Итого | 11 | 3280,25 |
|
|
|
| |
|
|
|
|
|
|
|
| |
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | ||
| Y-пересечение | 76,9764852 | 24,21156138 | 3,179327594 | 0,0098300668 | 23,02975528 | 130,9232151 | |
| Переменная X 1 | 0,920430553 | 0,279715587 | 3,290594434 | 0,008141843 | 0,29718579 | 1,543675827 | |
3. Оценку качества построенной модели дает коэффициент детерминации.
Коэффициент детерминации для линейной модели равен квадрату коэффициента корреляции
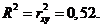
Это означает, что 52% вариации заработной платы (y) объясняется вариацией фактора x – среднедушевого прожиточного минимума.
Значимость уравнения регрессии проверяется при помощи F -критерия Фишера, для линейной парной регрессии он будет иметь вид
 , (1.21)
, (1.21)
где F подчиняется распределению Фишера с уровнем значимости a и степенями свободы k 1=1 и k 2= n –2.
В нашем случае
 .
.
Поскольку критическое значение критерия равно

и  , то признается статистическая значимость построенного уравнения регрессии. Отметим, что для линейной модели F - и t -критерии связаны равенством
, то признается статистическая значимость построенного уравнения регрессии. Отметим, что для линейной модели F - и t -критерии связаны равенством  .
.
4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Прогнозное значение yp определяется путем подстановки в уравнение регрессии (1.16) соответствующего (прогнозного) значения xp. В нашем случае прогнозное значение прожиточного минимума составит:  , тогда прогнозное значение прожиточного минимума составит:
, тогда прогнозное значение прожиточного минимума составит:

Средняя стандартная ошибка прогноза вычисляется по формуле:
 . (1.22)
. (1.22)
В нашем случае

Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:
 .
.
Доверительный интервал прогноза
 ,
,
или
 .
.
Выполненный прогноз среднемесячной заработной платы оказался надежным (g=0,95), но неточным, т.к. относительная точность прогноза составила 29,4/161,2×100%=18,2%.
 2018-02-14
2018-02-14 1627
1627
