Понятие о центральной предельной теореме

В центральной предельной теореме описываются условия, при которых возникает нормальный закон распределения. Оказывается, что он возникает всякий раз, когда случайная величина может быть представлена в виде суммы достаточно большого числа попарно независимых случайных величин, каждая из которых сравнительно мало влияет на всю сумму.

Пусть случайные величины 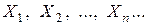(*) попарно независимы и каждая из них обладает математическим ожиданием и дисперсией: 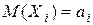, 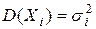. Обозначим через S_n сумму 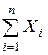, через А_n сумму 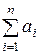, через B_n сумму .

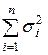Будем говорить, что к последовательности (*) применима центральная предельная теорема, если для любых чисел t ₁, t ₂, 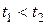при 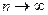справедливо предельное соотношение

, .

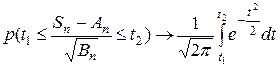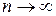Иными словами, при 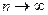случайная величина S_n имеет приближенно нормальное распределение с параметрами а = 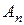и s =.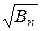

Теорема Ляпунова. В этой теореме устанавливаются достаточно общие условия, выполнение которых влечет применимость центральной предельной теоремы к последовательности (*). Эти условия охватывают большинство практических случаев.

Будем дополнительно предполагать, что у случайных величин Х_i существуют абсолютные центральные моменты третьей степени 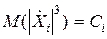. Если для последовательности (*) справедливо предельное соотношение 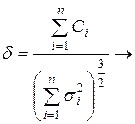0, 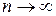, то для последовательности (*) справедлива и центральная предельная теорема.

Можно показать, что если 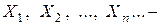одинаково распределенные и независимые случайные величины, то для последовательности (*) справедлива центральная предельная теорема.