Дополнительная тема. Уравнения Максвелла для стационарных электрического и магнитного полей

Вопросы к экзамену

по второй части двухсеместрового курса физики

(Электричество и магнетизм. Волновая и квантовая оптика)

1. Теорема Остроградского - Гаусса для электростатического поля.

2. Напряженность. Работа сил электростатического поля. Потенциал. Связь между потенциалом и напряженностью электростатического поля.

3. Магнитное поле. Закон Био-Савара-Лапласа. Индукция линейного и кругового тока.

4. Действие магнитного поля на проводник с током (закон Ампера) и на движущийся заряд (сила Лоренца).

5. Магнитный поток. Теорема Гаусса для магнитного поля. Явление электромагнитной индукции.

6. Электромагнитные колебания. Колебательный контур. Уравнение свободных незатухающих гармонических колебаний.

7. Электромагнитные колебания. Колебательный контур. Уравнение свободных затухающих гармонических колебаний.

8. Электромагнитные волны. Вектор Умова-Пойнтинга.

9. Волновая теория света. Интерференция света. Метод Юнга.

10. Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракция Френеля на круглом отверстии и на диске.

11. Дифракция света. Дифракция Фраунгофера на дифракционной решетке.

12. Дисперсия и поляризация света. Закон Малюса.

13. Корпускулярная теория света. Фотоэффект и эффект Комптона.

14. Тепловое излучение. Закон Кирхгофа. Закон Стефана-Больцмана. Закон смещения Вина. Квантовая гипотеза Планка.

15. Теория Бора для атома водорода. Постулаты Бора. Спектр атома водорода.

В случае стационарных (то есть неменяющихся во времени) электрического и магнитного полей, происхождение которых связано с покоящимися зарядами для электрического поля и со стационарными токами для магнитного поля, эти поля являются независимыми друг от друга, что позволяет рассматривать их отдельно друг от друга.

Уравнения Максвелла – это система уравнений, описывающих природу происхождения и свойства электрического и магнитного полей.

Уравнения Максвелла для стационарных полей:

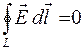I. ; II. ;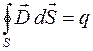

III.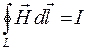; IV. .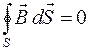

Рассмотрим каждое уравнение в отдельности.

I. 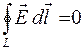, то есть циркуляция вектора напряженности 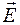электростатического поля по произвольному замкнутому контуру L равна нулю.

Циркуляцией вектора напряженности 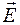электростатического поля по произвольному замкнутому контуру L называется интеграл

.

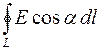Для того, чтобы найти циркуляцию вектора напряженности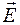по произвольному замкнутому контуру L, необходимо выбрать направление обхода контура, разбить этот контур L на элементы 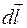, для каждого элемента 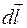рассчитать величину 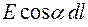(a – угол между векторам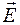и и 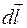), а затем все эти величины сложить, что приводит к искомому интегралу.

Однако для электростатического поля циркуляция вектора напряженности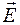по произвольному замкнутому контуру L может быть легко получена из формулы работы, совершаемой силами электростатического поля при перемещении пробного заряда q ₀по произвольному замкнутому контуру L.

С одной стороны, эта работа равна:

,

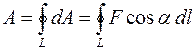а с учетом того, что 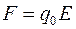эта работа равна: .

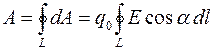С другой стороны, эта работа равна нулю, что следует из формулы работы:

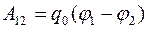, так как для замкнутого контура .

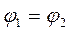Тогда и циркуляция вектора 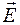по произвольному замкнутому контуру L тоже равна нулю, то есть: .

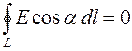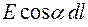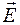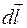Величина , где a – угол между векторами и может быть записана в виде скалярного произведения векторов 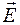и 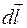, то есть, как 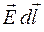, а полученное соотношение для циркуляции вектора 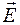примет вид:

.

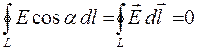II. 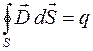, то есть поток вектора смещения 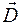электростатического поля через произ­вольную замкнутую поверхность S равен алгебраической сумме заключенных внутри этой поверхности зарядов q (q – заряд, являющийся источником электростатического поля).

Вектор электрического смещения 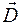определяется следующим образом:

.

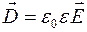Вектор электрического смещения 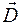введен для характеристики электростатического поля, так как модуль вектора 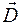, в отличие от модуля вектора напряженности 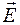, не изменяется при переходе из одной диэлектрической среды в другую.

Используя то, что в вакууме , теорема Остроградского-Гаусса для электростатического поля может быть записана следующим образом:

,

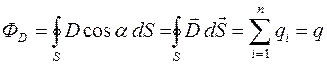то есть поток вектора смещения 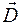электростатического поля через произвольную замкнутую поверхность S равен алгебраической сумме заключенных внутри этой поверхности зарядов.

III. 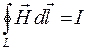, то есть циркуляция вектора 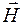по произвольному замкнутому контуру L равна алгебраической сумме токов I, охватываемых этим контуром L (I – стационарный ток, являющийся источником постоянного магнитногополя).

Уравнение III для циркуляции вектора напряженности 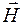магнитного поляследует из теоремы о циркуляции вектора магнитной индукции .

Циркуляцией вектора магнитной индукции по произвольному замкнутому контуру L называется интеграл: .

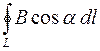Для того, чтобы найти циркуляцию вектора магнитной индукции по произвольному замкнутому контуру L необходимо выбрать направление обхода контура, разбить этот контур L на элементы 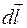, для каждого элемента 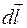рассчитать величину 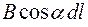(a – угол между векторами и 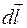), а затем все эти величины сложить, что приводит к искомому интегралу.

Однако согласно теореме о циркуляцию вектора циркуляция вектора по произвольному замкнутому контуру L равна произведению магнитной постоянной m ₀ на алгебраическую сумму токов, охватываемых этим контуром L:

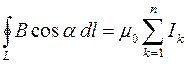, где

n – число проводников с токами, охватываемых контуром L. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему, а отрицательным – ток противоположного направления.

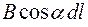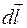Величина , где a – угол между векторами и может быть записана в виде скалярного произведения векторов и 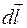, то есть, как 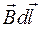, а полученное соотношение для циркуляции вектора примет вид:

.

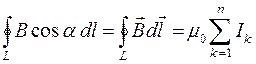Магнитное поле претерпевает изменения при переходе из одного вещества в другое, что определяется магнитными свойствами вещества, которые характеризуются величиной магнитной проницае­мости среды (m). Поэтому, кроме вектораиндукции магнитного поля, учитывающего магнитные свойства вещества, для описания магнитного поля введен также и вектор напряженности 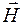магнитного поля, причем для однород­ной изотропной среды вектор магнитной индукции связан с вектором напряженности :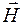

,

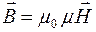где m ₀ – магнитная постоянная, m – магнитная проницае­мость среды.

Поскольку для вакуума m = 1, то с учетом приведенного соотношения может быть получена циркуляция вектора напряженности 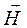по произвольному замкнутому контуру L в следующем виде:

,

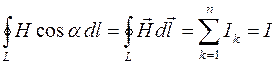то есть циркуляция вектора 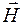по произвольному замкнутому контуру L равна алгебраической сумме токов, охватываемых этим контуром L.

IV. 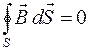, то есть поток вектора индукции магнитного поля через произвольную замкнутую поверхность S равен нулю (теорема Гаусса).

Векторные характеристики электростатического поля 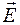и 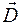, используемые в уравнениях Максвелла, связаны между собой следующим соотношением:

,

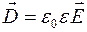где 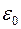– электрическая постоянная, e – диэлектрическая проницаемость среды.

Векторные характеристики магнитного поля и 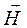, используемые в уравнениях Максвелла, связаны между собой следующим соотношением:

,

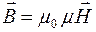где 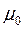– магнитная постоянная, 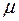– магнитная проницаемость среды.