Ранее рассматривалось понятие производной функции, ее
геометрический смысл, свойства, правила нахождения. Во многих технических задачах требуется решение обратной задачи: отыскание функции по заданной ее производной функции. Например,
задача об определении закона прямолинейного движения 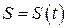 материальной точки по заданной ее скорости
материальной точки по заданной ее скорости 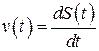 .
.
Решение сформулированной задачи основано на понятии
первообразной функции.
Определение. Функция 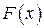 , определенная на промежутке
, определенная на промежутке 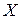 ,
,
называется первообразной функцией (или просто первообразной) для функции 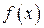 на
на 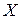 , если в любой точке этого промежутка функция
, если в любой точке этого промежутка функция 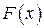 дифференцируема и имеет производную
дифференцируема и имеет производную 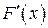 , равную
, равную 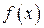 :
: 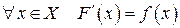 .
.
Пример. Функция 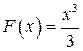 является первообразной для
является первообразной для 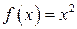 на
на 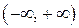 , так как для любого
, так как для любого  имеем
имеем 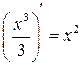 .
.
Для одной и той же функции существует бесконечное множество первообразных. Например, для 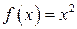 первообразными на
первообразными на 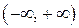 являются также функции
являются также функции 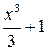 ,
, 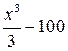 и вообще
и вообще 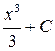 , где
, где 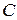 – произвольное число, поскольку
– произвольное число, поскольку 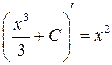 для любого
для любого  .
.
Аналогичные рассуждения верны и для первообразной произвольной функции 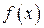 .
.
Свойства первообразных описываются легко проверяемыми теоремами.
Теорема 1. Если 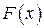 – первообразная для функции
– первообразная для функции 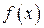 на
на 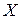 , то функция
, то функция 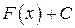 , где
, где 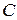 – произвольное число, также является первообразной для
– произвольное число, также является первообразной для 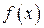 на
на 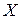 .
.
Теорема 2. Если 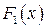 и
и 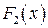 – произвольные первообразные для
– произвольные первообразные для 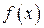 на
на 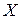 , то значение разности этих первообразных в каждой точке есть одно и то же число, т.е.
, то значение разности этих первообразных в каждой точке есть одно и то же число, т.е.  на
на 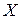 , где
, где 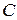 – некоторое число.
– некоторое число.
Теоремы 1 и 2 показывают, что если функция имеет первообразную 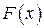 , то множество функций
, то множество функций 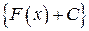 , где
, где  и
и 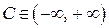 , образует множество всех первообразных для функции
, образует множество всех первообразных для функции 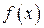 на
на 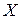 .
.
Для 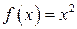 множество всех первообразных есть множество функций
множество всех первообразных есть множество функций 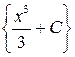 ,
, 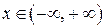 ,
, 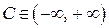 .
.
Определение. Множество всех первообразных для функции 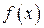 на промежутке
на промежутке 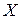 называется неопределенным интегралом
называется неопределенным интегралом
функции 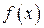 на
на 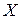 и обозначается символом
и обозначается символом 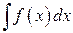 .
.
Выражение 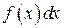 называется подынтегральным выражением,
называется подынтегральным выражением, 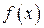 – подынтегральной функцией,
– подынтегральной функцией,  – переменной интегрирования,
– переменной интегрирования, 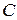 – произвольной постоянной. Процедуру отыскания
– произвольной постоянной. Процедуру отыскания
неопределенного интеграла функции называют интегрированием функции (будем говорить, что «интеграл вычисляется»).
Если 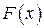 – какая-либо первообразная функции
– какая-либо первообразная функции 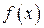 на
на 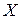 , то в силу определения неопределенного интеграла и свойств первообразных имеем
, то в силу определения неопределенного интеграла и свойств первообразных имеем 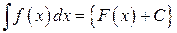 ,
,  ,
, 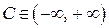 .
.
Для краткости это равенство записывается обычно в виде
 .
.
Пример. Проверить формулу 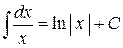 ,
,  или
или 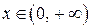 .
.
Решение. Используя определение абсолютной величины 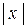 ,
,
можем записать 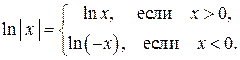
На интервале 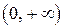 имеем
имеем 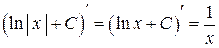 , поэтому для функции
, поэтому для функции 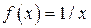 на
на 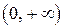 функция
функция 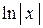 является первообразной.
является первообразной.
На интервале 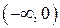 имеем
имеем 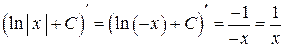 , поэтому для функции
, поэтому для функции 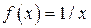 на
на 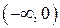 первообразная имеет вид
первообразная имеет вид 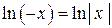 .
.
 2014-02-02
2014-02-02 6128
6128
