Для выработки инвестиционной политики главным является определение инвестиционной цели инвестора. Согласно современной теории портфеля цели инвестора проявляются в его отношении к риску и ожидаемой доходности. Одним из широко применяемых методов определения таких целей является построение кривой безразличия, характеризующей предпочтения инвестора. Это — кривая на критериальной плоскости, состоящая из оценок эквивалентных портфелей. Выбор между портфелями, оценки которых лежат на такой кривой, безразличен для инвестора (отсюда и название кривых). Вместе с тем сравнение портфелей, оценки которых лежат на разных кривых, свидетельствуют, что любой портфель с оценкой на одной кривой может быть предпочтительнее любого портфеля с оценкой на другой.
Кривая безразличия может быть представлена как двухмерный график: по оси абсцисс откладывается риск, мерой которого является стандартное отклонение, а по оси ординат — вознаграждение за риск, мерой которого является ожидаемая доходность.
На рисунке 4 представлены три кривые безразличия, каждая из которых представляет собой все возможные комбинации оценок инвестора в отношении риска и доходности портфелей.
Кривые безразличия имеют два важных свойства. Первое — все портфели, лежащие на одной кривой безразличия, являются равноценными. Портфели А и Б будут равноценными для инвестора, несмотря на то, что они имеют различные ожидаемые доходности
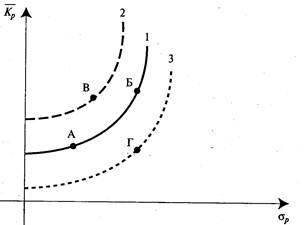
Рис. 4 Кривые безразличия инвестора.
и стандартные отклонения. При этом портфель Б имеет больший риск, чем портфель А, и с точки зрения этого параметра он хуже, зато портфель Б выигрывает в сравнении с портфелем А за счет более высокой ожидаемой доходности.
Второе важное свойство кривых безразличия: любой портфель, лежащий на кривой безразличия, расположенной выше и левее, более привлекателен для инвестора по сравнению с портфелем, лежащим на кривой, находящейся ниже и правее. Портфель В, который лежит на кривой безразличия 2, находящейся выше и левее кривой 1, имеет большую доходность, чем портфель А, что компенсирует его больший риск, но в то же время у портфеля В меньший риск, чем у портфеля Б, что компенсирует его меньшую ожидаемую доходность. Поэтому портфель В предпочтительнее для инвестора по сравнению с портфелями А и Б. В силу описанных свойств кривых безразличия они, естественно, не пересекаются.
Исходя из отношения к риску и доходности и их оценок, инвестор может иметь бесконечное число кривых безразличия. Эти кривые проходят через каждую точку критериальной плоскости, целиком заполняя ее. Характер расположения кривых означает индивидуальную для инвестора взаимозаменяемость доходности и риска. Крутые кривые безразличия означают более осторожного инвестора, чем пологие кривые (рис. 5).
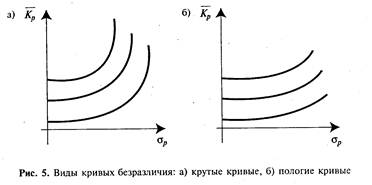
В первом случае инвестор готов допустить малое увеличение риска лишь с компенсацией в виде значительного увеличения доходности. Во втором — инвестор ради небольшого увеличения доходности готов принять значительное увеличение риска.
Таким образом, менеджер в работе по формированию и управлению портфелем должен определить ожидаемую доходность и риск для каждого потенциального портфеля, построить график и затем выбрать один портфель, который лежит на кривой безразличия, расположенной выше и левее относительно других кривых.
При выборе портфеля на базе кривых безразличия менеджер, исходит из двух предположений: о ненасыщаемости и избежании риска. Предполагается, что инвестор всегда предпочитает увеличение уровня своего благосостояния. Инвестор, делающий выбор между двумя одинаковыми во всем (кроме ожидаемой доходности) портфелями, выберет портфель с большей ожидаемой доходностью. Однако если инвестору нужно выбрать между портфелями, имеющими одинаковый уровень ожидаемой доходности, но разную степень риска, он выберет портфель с меньшим риском.
Главными параметрами при управлении портфелем, которые необходимо определить менеджеру, являются его ожидаемая доходность и риск. Формируя портфель, менеджер не может точно определить будущую динамику его доходности и риска, поэтому свой инвестиционный выбор он строит на ожидаемых значениях. Данные величины оцениваются на основе статистических отчетов за предыдущие периоды времени. Полученные оценки менеджер может корректировать согласно своим ожиданиям развития будущей конъюнктуры.
Поскольку портфель, формируемый инвестором, состоит из набора различных ценных бумаг, ожидаемая доходность и риск портфеля должны зависеть от ожидаемой доходности и риска каждой отдельной ценной бумаги. Кроме того, ожидаемая доходность портфеля зависит от размера начального капитала, инвестированного в данные ценные бумаги.
Ожидаемая доходность портфеля Кр может быть вычислена двумя способами. Первый способ основан на использовании стоимостей на конец периода и заключается в вычислении ожидаемой цены портфеля в конце периода и уровня его доходности:
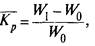
где Wx — ожидаемая стоимость портфеля в конце периода; WQ — начальная стоимость портфеля.
Второй способ построен на использовании ожидаемой доходности ценных бумаг, которая вычисляется как средневзвешенная ожидаемых доходностей ценных бумаг, входящих в портфель. Относительные рыночные курсы ценных бумаг портфеля используются в качестве весов.
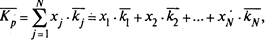
где хj — доля начальной стоимости портфеля, инвестированная в ценную бумагу j;
kj — ожидаемая доходность ценной бумаги j;
N — количество ценных бумаг в портфеле.
Инвестор, который желает получить наибольшую возможную ожидаемую доходность, должен иметь портфель, состоящий из одной ценной бумаги, у которой ожидаемая доходность наибольшая. Однако менеджер посоветует инвестору диверсифицировать свой портфель, т.е. включить в него несколько ценных бумаг, снижая тем самым риск.
Диверсификация — сознательное комбинирование ценных бумаг, при котором достигается не просто их разнообразие, но и определенная взаимосвязь между доходностью и риском. Применение диверсификации позволяет снизить инвестиционные риски по портфелю.
Существует ряд рисков, связанных с ценными бумагами:
• общий риск — представляет собой совокупность всех рисков, связанных с осуществлением финансовых инвестиций;
• рыночный (систематический) риск — возникает под влиянием общих факторов, затрагивающих рынок в целом, и охватывает все предприятия, представленные на рынке. Этот риск нельзя устранить диверсификацией;
• специфический (несистематический) риск — возникает под воздействием уникальных, специфических для отдельного предприятия факторов и влияет на доходы отдельных ценных бумаг. Этот риск может быть сокращен путем диверсификации.
Инвестиционный риск портфеля определяется как изменчивость доходности, которая измеряется стандартным отклонением (дисперсией) распределения доходности портфеля.
Ожидаемый риск портфеля представляет собой сочетание стандартных отклонений (дисперсий) входящих в него ценных бумаг. Однако в отличие от ожидаемой доходности риск портфеля не является обязательно средневзвешенной величиной дисперсий доходности ценных бумаг. Различные ценные бумаги могут по-разному реагировать на изменение конъюнктуры рынка, в результате стандартные отклонения их доходности в ряде случаев будут гасить друг друга, что приведет к снижению риска портфеля. Риск портфеля зависит от того, в каком направлении и в какой степени меняются доходности входящих в него ценных бумаг при изменении конъюнктуры рынка.
Для определения степени взаимосвязи и направления изменения доходностей ценных бумаг используют показатели ковариации и коэффициента корреляции.
Показатель ковариации доходности ценных бумаг (COVxу) определяется по формуле
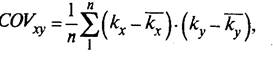
где кх — норма дохода по ценной бумаге х;
кх — ожидаемая норма дохода по ценной бумаге х;
ку — норма дохода по ценной бумаге у;
ку — ожидаемая норма дохода по ценной бумаге у;
п — количество вариантов (наблюдений) за доходностью ценных бумаг.
При положительном значении ковариации доходность ценных бумаг изменяется в одном направлении, при отрицательном — в обратном, при нулевом значении ковариации взаимосвязь между доходностями активов отсутствует.
Другим показателем степени взаимосвязи изменения доходностей ценных бумаг служит коэффициент корреляции (rху). Он рассчитывается по формуле
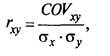
где σх — стандартное отклонение доходности ценной бумаги х;
σу — стандартное отклонение доходности ценной бумаги у.
Коэффициент корреляции изменяется в пределах от -1 до +1. При положительном значении коэффициента доходности ценных бумаг изменяются в одном направлении с изменением конъюнктуры, при отрицательном — в противоположном. При нулевом значении коэффициента корреляция связь между доходностями ценных бумаг отсутствует.
Риск портфеля, состоящего из двух ценных бумаг, рассчитывается по формуле
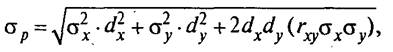
где σ р — стандартное отклонение по портфелю;
dx — доля ценной бумаги х в портфеле;
dy — доля ценной бумаги у в портфеле;
rху — коэффициент корреляции между ценными бумагами х и у.
Риск портфеля, объединяющего в себе большее число ценных бумаг, требует построения ковариационной матрицы с данными о дисперсии и ковариации бумаг и ее решения.
Часто на практике используется модель ценообразования на капитальные активы (САРМ), в основе которой лежит предположение, что норма дохода по рисковому активу складывается из нормы дохода по безрисковому активу (безрисковой ставки) и премии за риск, которая связана с уровнем риска по данному активу.
Фундаментальное допущение, лежащее в основе данной модели, состоит в том, что та часть ожидаемого дохода по ценной бумаге, которая приходится на премию за риск, является функцией связанного с данной ценной бумагой систематического риска. Поскольку специфический риск легко можно устранить диверсификацией портфеля, с точки зрения рынка он не является необходимым и рынок «не вознаграждает» инвестора за этот риск; вознаграждение за риск зависит только от систематического риска.
Для измерения величины систематического риска существует специальный показатель — бета-коэффициент. Он характеризует неустойчивость (изменчивость) дохода отдельной ценной бумаги относительно доходности рыночного портфеля. Рассчитать бета-коэффициент можно, используя следующую формулу:
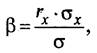
где rx — корреляция между доходностью ценной бумаги х и средним уровнем доходности ценных бумаг на рынке;
σ — стандартное отклонение доходности по рынку ценных бумаг в целом.
Уровень риска отдельных ценных бумаг определяется на основе значений бета-коэффициента следующим образом:
β= 1 — средний уровень риска;
β > 1 — высокий уровень риска;
β < 1 — низкий уровень риска.
По портфелю бета-коэффициент рассчитывается как средневзвешенный коэффициент отдельных видов входящих в портфель ценных бумаг, где в качестве весов берется их удельный вес в портфеле.
 2014-02-02
2014-02-02 1183
1183
