 Осью называется прямая с заданным началом отсчета и направлением (направление на рисунках указывается стрелкой).
Осью называется прямая с заданным началом отсчета и направлением (направление на рисунках указывается стрелкой).
Проекцией точки А на ось 0 u называется точка А 1 пересечения оси и плоскости 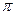 , перпендикулярной этой оси и проходящей через точку А (рис. 2.3).
, перпендикулярной этой оси и проходящей через точку А (рис. 2.3).
Векторной проекцией вектора 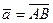 на ось 0 u называется вектор
на ось 0 u называется вектор 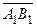 , где А 1, В 1 – проекции точек А, В на ось 0 u.
, где А 1, В 1 – проекции точек А, В на ось 0 u.
Числовой проекцией (или просто проекцией) вектора 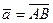 на ось 0 u называется число, равное:
на ось 0 u называется число, равное:
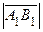 , если вектор
, если вектор 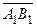 и ось 0 u одинаково направлены (рис. 2.4,а);
и ось 0 u одинаково направлены (рис. 2.4,а);
–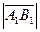 , если вектор
, если вектор 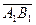 и ось 0 u направлены противоположно (рис. 2.4,б);
и ось 0 u направлены противоположно (рис. 2.4,б);
0, если и ось 0 u  перпендикулярны.
перпендикулярны.
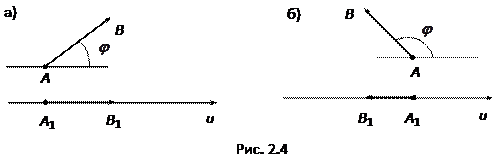
Обозначается проекция вектора на ось 0 u символом: 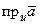 . Из определения следует, что
. Из определения следует, что
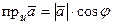 , (2.1)
, (2.1)
где 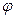 – угол между положительным направлением оси 0 u и вектором
– угол между положительным направлением оси 0 u и вектором 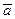 .
.
Таким образом, если угол 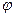 острый, то проекция вектора на ось положительна, если
острый, то проекция вектора на ось положительна, если 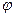 тупой угол, то проекция отрицательна; если
тупой угол, то проекция отрицательна; если 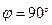 , то проекция равна нулю.
, то проекция равна нулю.
Вектор 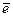 называется единичным, если
называется единичным, если 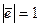 .
.
Единичный вектор 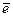 , направление которого совпадает с направлением оси 0 u, называется направляющим вектором этой оси или ортом оси. Если
, направление которого совпадает с направлением оси 0 u, называется направляющим вектором этой оси или ортом оси. Если 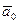 – единичный вектор, сонаправленный с вектором
– единичный вектор, сонаправленный с вектором 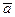 , то
, то 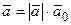 , если
, если 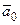 направлен противоположно вектору
направлен противоположно вектору 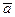 , то
, то  .
.
 Свойства проекций
Свойства проекций
1°. Проекция на ось суммы векторов равна сумме проекций этих векторов, т.е.
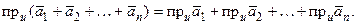 (2.2)
(2.2)
2°. Проекция произведения вектора на число равна произведению этого числа на проекцию вектора, т.е.
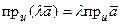 . (2.3)
. (2.3)
 2014-02-02
2014-02-02 9018
9018
