Доходы от операций с корпоративными ценными бумагами

При определении доходности корпоративных финансовых инструментов важно деление их на ценные бумаги с фиксированным либо изменяющимся уровнем дохода. Ценные бумаги с фиксированным уровнем дохода (облигации, привилегированные акции) обеспечивают инвестору получение заранее установленной величины дохода. Присутствие корпоративных облигаций на российском рынке в настоящее время крайне незначительно. Так, в 1998 г. соотношение акций и облигаций составляло 99:1, поскольку эмитенты предпочитают привлекать капитал на безвозвратной основе (акции, а не облигации) и неохотно берут обязательства по выплате фиксированных процентов (при относительно высоком уровне ставки ссудного процента). Кроме того, у банков, выступающих активными эмитентами, существует возможность более простыми способами привлекать заемные средства (выпуск векселей, депозитных и сберегательных сертификатов и т. п.).

Доходность облигаций до срока погашения оценивают в зависимости от их инвестиционных качеств и текущего рыночного курса. Определение соответствующей доходности основано на применении рассмотренных ранее динамических методов, в частности метода NPV - чистой приведенной стоимости (капитализации дохода), в соответствии с которым стоимость любого финансового актива представляется как современная (текущая) стоимость будущих платежей, поступающих от его использования. Стоимость, по которой потенциальный инвестор готов приобрести облигацию, может быть определена по формуле

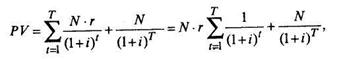
где N - номинальная стоимость облигации;

r - ставка купонного процента;

i - ставка дисконтирования, т. е. норма текущей доходности, выбираемая инвестором как наилучшая из альтернативных возможностей вложения капитала;

T - срок погашения, т.е. период, в течение которого компания должна возместить владельцу ее номинальную стоимость.

Эта формула называется основной моделью оценки облигаций (Basic Bond Valuation Model). Ее экономический смысл состоит в том, что текущая стоимость облигации равна сумме всех процентных выплат за период ее обращения и номинала, приведенных к настоящему моменту времени, т. е. дисконтированных по норме текущей доходности для данного вида облигаций. При этом предполагается, что норма текущей доходности - ожидаемая инвесторами минимально необходимая величина доходности по альтернативным безрисковым инвестициям и премия за риск. Отсюда текущая стоимость облигации - предписываемая ей инвестором стоимость, по которой он желал бы ее приобрести. Если в качестве коэффициента дисконтирования используется рыночная норма доходности, т.е. средняя из ожидаемых значений доходности отдельными инвесторами (это определяет соотношение спроса и предложения на данную облигацию), то текущую стоимость облигации можно рассматривать в качестве рыночной цены.

Пример. Пусть инвестору необходимо определить текущую стоимость облигации номиналом 1,0 тыс. руб., ставкой купонного дохода 30% и сроком обращения 10 лет, которая бы обеспечила ему получение 35% годового дохода (на уровне рыночной нормы доходности).

Подставляя эти величины в формулу текущей стоимости облигации, получим:

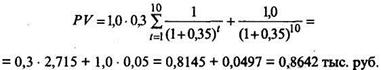
Значения дисконтирующих множителей приведены в финансовых таблицах.

В данном случае текущая цена облигации равна 0,8642 тыс. руб., что меньше ее номинала, и облигация продается с дисконтом, что то же самое. Некий совокупный инвестор готов приобрести данную облигацию только по цене ниже номинала.

Допустим, что рыночная норма доходности по данной облигации составляет 25% годовых (при прочих равных условиях). Тогда ее текущая рыночная цена

В данном случае текущая себестоимость облигации превышает ее номинал, и она может быть приобретена инвестором с премией.

Таким образом, можно отметить, что чем больше ожидаемый уровень дохода по облигации с позиции инвестора, т.е. рыночная норма доходности превышает установленную процентную ставку купонного дохода, тем ниже рыночная цена облигации, и наоборот. При равенстве ожидаемого уровня дохода купонной ставки рыночная цена облигации близка к номиналу.

В случае облигации с нулевым купонным доходом, т. е. без выплаты процентов в период обращения, инвестор может определить ее текущую стоимость:

где N - номинал облигации, руб.;

Т - период ее обращения, лет;

i - ожидаемая инвестором норма доходности, %,

Текущая стоимость облигации представляет здесь величину номинала, которую получит владелец при погашении облигации эмитентом и которая приведена к настоящему (текущему) моменту по ставке дисконтирования, равной ожидаемой норме доходности. При этом ожидаемая инвестором норма доходности определяется на уровне не ниже доходности альтернативных вложений. Эта формула представляет упрощенный случай основной модели оценки облигаций.

Пример. Пусть инвестору необходимо определить текущую стоимость облигации номиналом 1,0 тыс. руб. и сроком обращения пять лет при условии, что ожидаемая норма доходности составит 20% годовых. Подставляя значения в формулу текущей стоимости облигации, получим:

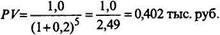
Стоимость, равная 402 тыс. руб., представляет максимальную цену, которую инвестор захочет заплатить, или минимальную цену, по которой он захочет продать, если он ожидает от инвестиций данного типа доходность в размере 20%. Такую облигацию следует купить только при цене существенно ниже номинала (с дисконтом). Допустим, что рыночная цена такой облигации составляет 0,35 тыс. руб. Тогда доходность данной облигации при условии, что инвестор приобрел ее по рыночной цене Р, будет определяться:

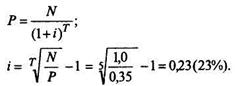
Расчет показывает, что приобретение такой облигации - выгодное вложение капитала, поскольку норма дохода, обеспечиваемая ею (23%), больше альтернативной (20%).

Зная текущую рыночную стоимость облигации, ее номинал, купонную ставку дохода и срок до погашения, можно определить и внутреннюю норму доходности, т.е. значение доходности, меньше которого владение облигацией будет убыточно.

Существуют компьютерные программы, позволяющие выполнять подобные расчеты. В общем виде норма доходности (Profitability Index) определяется как показатель, характеризующий соотношение дисконтированных потоков поступлений и платежей в течение инвестиционного периода Т:

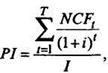
где PI - ожидаемая доходность инвестиций;

NCF, - чистый денежный поток в период времени t;

I - величина единовременных вложений средств в приобретение финансовых активов;

i - ожидаемая инвестором норма доходности (ставка дисконтирования), %.

Задача определения доходности от инвестирования средств в обыкновенные и привилегированные акции является более сложной, чем в облигации, поскольку существует значительная неопределенность в оценке величины будущих поступлений денежных средств по данным видам ценных бумаг.

По сравнению с позицией владельца обыкновенных акций позиция инвестора, обладающего привилегированными акциями, более благоприятна при выплате дивидендов, а также возврате первоначальной суммы инвестиций в случае ликвидации предприятия. При определении стоимости привилегированных акций единственно точно определяемым элементом служит ежегодный фиксированный дивиденд.

Величина текущей стоимости привилегированных акций представляет с позиций инвестора величину потока ожидаемых в будущем дивидендов, дисконтированных по приемлемой для инвестора норме доходности, т.е.

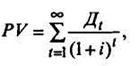
где PV - текущая стоимость привилегированной акции, используемой неопределенное число лет;

Д - величина дивидендов, планируемых к получению в t-м году;

i - норма текущей доходности.

В случае неопределенно долгого владения привилегированной акцией для определения ее текущей стоимости может использоваться следующая упрощенная формула:

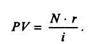
Рассчитанная таким образом величина определит цену, которую инвестор пожелает заплатить за привилегированную акцию, или минимальную цену, за которую он согласится продать акцию. Как правило, ни один инвестор не планирует держать у себя бесконечно долгое время конкретную ценную бумагу, поскольку возникают возможности для более выгодного использования средств. Если инвестор может надеяться продать акцию по определенной цене в известное время, то норму доходности такой акции можно определить:

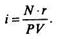
Инвестирование средств в обыкновенные акции должно обеспечить ожидаемый в будущем поток движения наличности, состоящий из величины предполагаемых в каждом году дивидендов и цены, которую инвесторы надеются получить при продаже акции в конце некоторого периода и которая включает прибыль от первоначального инвестирования и доход с прироста капитала (либо потери капитала). Планируемый период владения акциями у различных инвесторов может сильно различаться. Те из них, которые хранят их долго, ожидают будущие дивиденды и возможность продать акции по цене выше той, которую они заплатили. Эта конечная стоимость будет зависеть от желания в этот момент других инвесторов купить предложенные акции. Цена, которую они готовы заплатить, в свою очередь, будет зависеть от ожиданий дивидендного дохода и конечной стоимости.

Общая величина дохода всей цепи инвесторов, вкладывающих свои средства в акции, представляет сумму распределений со стороны компании наличных средств - будь то наличные дивиденды, ликвидационные дивиденды или выплаты в процессе выкупа акций, т.е. любое распределение денежных средств акционерам, включая выкупы акций. Акционеры ожидают, что, реинвестируя получаемую прибыль, компания увеличивает будущую прибыльность их вложений и предельный размер дивидендов.

Если инвестор предполагает держать акцию один год и цена акции будет расти при ставке g, то текущая стоимость такой акции будет:

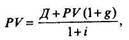
где Д - ожидаемый в конце года дивиденд;

g - темп роста акции в течение года, %;

i - ставка дисконтирования.

Отсюда

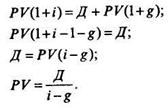
Данное выражение представляет собой текущую стоимость ожидаемых дивидендов и цену акции в конце года, дисконтированную при соответствующей норме прибыли i. Так, если в прошлом году компания выплатила на акцию 10 руб. дивидендов, причем прибыли компании и соответственно дивиденды росли в среднем на 5 % ежегодно за ряд лет, то инвестор, предполагая, что темп роста сохранится и цена акции также возрастет на 5%, может определить ожидаемую величину дивиденда:

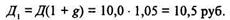
Если предположить, что норма прибыли по аналогичным акциям равна 12%, то можно определить ее текущую стоимость:

РV = 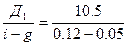=150 руб.

Если фактическая цена акции выше, то инвестор не купит ее, либо, если владеет акцией, продаст ее.

Ожидаемую норму прибыли на данную акцию можно определить из условия

где i - ожидаемая норма прибыли.

Отсюда

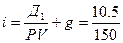+ 5% = 7% + 5% =12%.

Таким образом, если инвестор ожидает получить дивиденд в 10 руб. и цена акции увеличится предположительно на 5%, то ожидаемая общая прибыль составит 12%, из которых 7% - ожидаемый доход от дивиденда и 5% - ожидаемый доход от прироста капитала. Обычно ожидаемая норма прибыли равна требуемой (приемлемой), т.е. коэффициенту дисконтирования, используемому при расчете текущей рыночной цены акции, при условии, что рынок акций находится в равновесии. Если бы период владения акциями составлял некоторое число лет Т, то текущая стоимость акции, т.е. дисконтированный к настоящему моменту поток будущих поступлений от владения акцией, составлял бы:

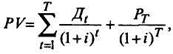
где Д _t - ожидаемые дивиденды в конце периода;

Р_t - ожидаемая стоимость акции в конце периода Т.

Ожидаемый уровень дохода инвестора будет представлять такую норму доходности (ставку дисконтирования), которая уравняет текущую стоимость акции, т.е. дисконтированную величину получаемых дивидендов и ожидаемой будущей стоимости акции с ее рыночной стоимостью Р_о. Он представляет такое пороговое значение доходности, ниже которого владение акцией было бы убыточным для инвестора (с позиций его ожиданий будущих поступлений по акции):

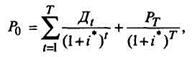
где i * - ожидаемый уровень доходности (норма дисконтирования).

Для решения подобных уравнений существуют компьютерные программы и специальные калькуляторы.

Для индивидуального инвестора владение акциями может быть неопределенно долгим, и тогда модель оценки соответствующей акции аналогична модели бессрочной облигации. В этом случае ожидаемый доход, т.е. поток наличности, целиком состоял бы из будущих дивидендов и уровень дохода определялся бы путем решения следующего уравнения относительно:

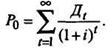
Существует, однако, большая неопределенность получения дивидендов по акциям, чем процентов по облигациям, и предсказывать их сложнее, чем выплаты процентов по облигации, что делает оценку обыкновенной акции более сложной, чем облигации.

Уравнение представляет общую модель оценки акции в том смысле, что величина ожидаемых дивидендов в момент t может изменяться любым образом в зависимости от экономического положения компании-эмитента, при этом уравнение будет действительно. В соответствии с ожидаемой динамикой дивидендов базовая модель оценки акций может изменяться. Возможны следующие случаи изменения ожидаемых значений дивидендов:

1) величина дивидендов не меняется со временем (модель дисконтирования дивидендов при нулевом росте);

2) величина дивидендов возрастает с постоянным темпом. Если темп роста обозначить как g, то дивиденды, получаемые в момент t, можно представить как Д_t = Д_t-1 (1 + g) или Д_t = Д_о (1 + g)^t. Тогда текущая стоимость акции (дисконтированное значение потока ожидаемых поступлений дивидендов) будет:

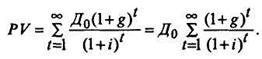
Если i > g (в противном случае в результате получится отрицательное значение стоимости акции, что бессмысленно) и g - постоянная величина, то

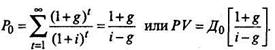
Отсюда

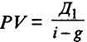так как Д₁ = Д₀ (1 + g).

Если ожидается, что дивиденды компании будут расти постоянными темпами, то величина ожидаемого дохода, определяемая из условия равенства текущей стоимости будущих поступлений по акции и ее текущей цены приобретения, может быть рассчитана следующим образом:

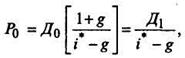
откуда

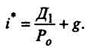
Предположим, что в течение последнего года компания "Мир" выплачивала дивиденды из расчета 10 руб. на акцию. Прогнозируется, что выплаты дивидендов возрастут на 5% в год на неопределенное время в будущем. Приемлемая норма доходности для инвесторов составляет 11%, а рыночная цена акции "Мир" равна 250 руб. Текущая стоимость одной акции "Мир" составляет:

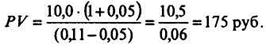
Сравнив ее с рыночной ценой Р_о

NPV = PV - Р_о = 175 - 250 = -75 руб.,

видим, что с позиций инвестора, оценившего акцию в 175 руб., акции компании "Мир" переоценены рынком, и инвесторы будут стремиться их продать, если владеют ими в настоящее время. Норма ожидаемой доходности такой акции

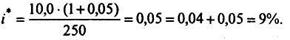
Итак, приемлемая для инвестора норма доходности превосходит ожидаемую (11 % > 9%);

3) оценка акций с изменяющимся темпом роста дивидендов. Эта модель оценки акций отражает наиболее общий случай определения их текущей стоимости и ожидаемого дохода инвесторов, вкладывающих средства в приобретение таких акций.

Допустим, что до некоторого периода Г дивиденды изменяются с различным темпом, после момента Т - постоянно возрастают на величину g, т. е.

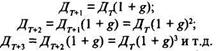
Текущая стоимость прогнозируемого потока дивидендов может быть определена путем деления потока платежей на две части, нахождения стоимости PV длякаждой из них и затем сложения обеих частей потока. Текущая стоимость ожидаемых дивидендов в период до момента Т может быть рассчитана следующим образом:

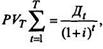
где Д_t - ожидаемая величина дивидендов в момент времени t;

i - приемлемая норма доходности (коэффициент дисконтирования) для инвестора.

Затем можно определить текущую стоимость потока ожидаемых дивидендов в момент Т, используя модель постоянного роста и принимая за начальный момент t _о, к которому осуществляется приведение значений будущего потока дивидендов, точку Т- t_o, т. е.

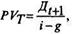
где Д_t+1 - ожидаемая величина дивидендов в момент времени t+1.

Одновременно с этим PV_T представляет ожидаемую величину текущей стоимости всего потока дивидендов, ожидаемых в период времени после Т, т.е. Д_t+1, Д _t+2 и т.д. Значение текущей стоимости ожидаемого потока дивидендов после момента T(PV_T) оцененное в начальный момент прогнозирования в точке t = 0 (дисконтированное), можно представить в виде

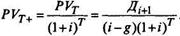
Общая величина текущей стоимости всего потока дивидендов, ожидаемых к получению до и после момента Т (оцененная в точке t = 0), может быть представлена как сумма двух составляющих:

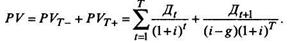
Ожидаемая норма доходности (внутренняя норма доходности) вложения средств в подобные акции определится из условия безубыточности для инвесторов, т. е. равенства текущей стоимости ожидаемого потока дивидендов PV и стоимости приобретения (рыночной цены) акций:

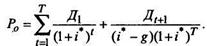
Вывести в общем виде формулу расчета внутренней нормы доходности инвестиций i* за весь прогнозируемый период из уравнения (3) невозможно, однако можно сосчитать ее подбором значений, используя метод "проб и ошибок", либо с помощью компьютерных программ.

Допустим, что в течение прошлого года компания "Темп" выплачивала дивиденды из расчета 5 руб. за акцию. В следующем году предполагается платить дивиденды 13,5 руб. за акцию. Темп роста дивидендов

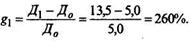
Еще через год величина дивидендов ожидается в 20 руб. за акцию, темп роста

Одновременно предполагаемый рост дивидендов в будущем, начиная со второго года, составит 10% ежегодно, а приемлемая норма доходности для инвесторов определяется в 15%. Величина дивидендов в будущем Д _{t +1} = Д₃ = 20,0 (1+0,1) = 22 руб.

В результате величина текущей стоимости потока дивидендов соответственно

в течение первых двух лет

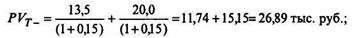
в течение последующего периода

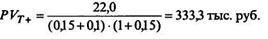
Общая величина текущей стоимости акций

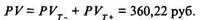
Учитывая, что текущая рыночная стоимость акций компании "Темп" достигает 370 руб. за штуку, можно отметить, что они переоценены рынком. Однако поскольку значения PV и Р_о различаются незначительно (360,22 и 370 руб.), то они находятся вблизи равновесной цены и рынок данных акций можно считать уравновешенным.

Ожидаемую доходность владельцев этих акций можно определить по формуле

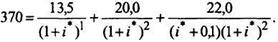
Ранее, используя ставку дисконтирования в 15%, получили результат 360,22 руб. Если принять ожидаемую норму доходности равной 14,8%, получим результат, равный 376,12 руб. Это значит, что i * должна находиться в интервале от 14,8 до 15%. При значении i * = 14,85% получаем результат Р_о = 370,65 руб., наиболее близкий к заданному. Отсюда можно сделать вывод, что ожидаемая норма доходности для данных акций составит 14,85% и будет близка к рыночной, приемлемой для инвесторов (15%).

Следует отметить, что в настоящее время в условиях кризиса российского фондового рынка целью совершения большинства операций с ценными бумагами является получение не инвестиционной, а спекулятивной доходности, т.е от разницы в ценах покупки и продажи.