Горные породы в земной коре в естественном залегании находятся в напряженном состоянии, которое обусловлено действием двух силовых полей – гравитационного и тектонического, а также влиянием температурных градиентов и геохимических процессов.
Реальный массив горных пород представляет собой сложную среду. Напряженное состояние его создается при формировании горных пород: магматических – при остывании и раскристаллизации магмы; осадочных – при гравитационном уплотнении осадков; метаморфических – при перекристаллизации первичных пород.
Механические свойства пород в массиве разнятся между собой в весьма широких пределах – от плывунов до весьма крепких изверженных пород (к примеру, кварциты). Поведение пород при проведении выработок и разработке месторождений также многообразно – от микроподвижек до горных ударов.
Деформирование и разрушение горных пород изучает механика подземных сооружений, которая оперирует механическими моделями. Механические модели "идеализируют" массив пород, в них отражаются только главные существенные его свойства и отбрасываются факторы, которые с точки зрения исследуемых явлений несущественны. К числу свойств массива пород, которые подвергаются схематизации в модели, помимо прочностных и деформационных, относятся сплошность, изотропность и однородность.
Под моделью понимается такая система (представляемая мысленно или материально реализуемая в аналог), которая, отображая или воспроизводя объект исследования, способна замещать его так, что ее изучение дает новую информацию об этом объекте. К моделированию прибегают в случаях невозможности непосредственного изучения объекта или явления (большие габариты, длительность протекания процессов, сложность системы и пр.).
В зависимости от механических свойств массива пород и характера протекающих в нем процессов используются различные модели, которые в совокупности охватывают многообразие массивов пород и исследуемых явлений. Наиболее широко применяются следующие модели массива пород: упругая, вязкоупругая, упруго- и жесткопластическая (в том числе неоднородная), вязкоупругопластическая, текучая (вязкая), раздельно-блочная (зернистая) и др.
При использовании упругой модели взаимодействия пород и крепи массив принимается как упругая сплошная среда. В основу упругой модели положено свойство упругости горных пород восстанавливать форму и размеры при разгрузке.
Упругая модель наиболее применима в следующих случаях:
1) контур выработки не является вполне разгруженным;
2) закрепленная выработка испытывает влияние соседней выработки;
3) исследуется характер взаимодействия крепи с неоднородным массивом горных пород;
4) исследуется взаимодействие с массивом крепи выработок некруглого сечения и др.
Упругая модель массива пород представляет собой линейно-деформируемую среду, т е. среду, в которой напряжения и деформации связаны линейными зависимостями. В упругой модели качества реальных массивов пород идеализированы. Деформации могут быть описаны законом Гука (массив представлен структурной схемой в виде пружины):
σ = E ∙ζ,
где σ – растягивающее напряжение; E – модуль упругости; ζ – деформация пружины.
В случаях объемного напряженного состояния, характерного для массива пород, обобщенный закон Гука имеет следующий вид:
ζ x = 1/ E [ σх – μ(σ y +σ z)];γ xy = τ xy /σ;
ζ y = 1/ Е [σ y – μ(σ z +σ x)];γ yz = τ yz /σ;
ζ z = 1/ Е [σ z – μ(σ x +σ y)];γ xz = τ xz /σ,
где – ζ x, ζ y, ζ z – линейные деформации в направлении нормальных напряжений; γ xy, τ yz, τ xz – деформации сдвига.
Приведенные выражения справедливы для изотропной среды. В качестве модели массива пород используются анизотропные упругие, разномодульные среды.
При использовании вязкоупругой модели взаимодействия пород и крепи учитывается влияние реологических факторов, а массив горных пород моделируется средой, обладающей свойством ползучести горных пород, т.е. способностью пород деформироваться во времени при постоянной нагрузке, а также свойства релаксации напряжений, т.е. изменения напряжений при фиксированной деформации. В начальный момент в среде при ступенчатом нагружении возникают упругие мгновенные деформации, а затем во времени развиваются деформации ползучести.
Вязкоупругие модели и модели, включающие вязкий элемент, и их уравнения состояния называются также реологическими ("рео"- с греческого "течь"). При описании экспериментов используются теория наследственной ползучести, теория упрочнения, теория течения и теория старения.
Напряжения в материале описываются одним из следующих уравнений:
σ = H [ζ0+(σ/ H− ζ0)exp(−t / n)].
При t →∞ напряжения в материале убывают, стремясь к постоянной величине Н ζ0 (происходит релаксация напряжений).
Крепь может быть жесткой, упругой или также обладать свойством ползучести. Наибольшее распространение получила теория наследственной ползучести горных пород.
Вязкопластическая модель применяется при решении задачи о выдавливании пород в выработку, задачи опускания столба пород над выработкой, задачи прогноза смещения пород в подготовительных выработках и др.
В упругопластической модели взаимодействия пород и крепи учитываются упругие деформации пород за пределами зоны неупругих деформаций. Модель разработана для случаев, когда массив обладает только внутренним трением и сцеплением, идеальной пластичностью, линейным и степенным упрочнением, реальными свойствами и др.
До некоторого предела, определяемого условиями предельного состояния:
σ1=σсж+ βσз ,
 (σ x −σ y)2+4τ2 xy =(σ x +σy+2 A)2sin2φ,
(σ x −σ y)2+4τ2 xy =(σ x +σy+2 A)2sin2φ,
|
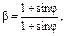 а A=K ctg φ,
а A=K ctg φ, в модели развиваются только упругие деформации, а по достижении указанного предела – пластические. В соответствии с этим в массиве пород выделяются упругая и пластическая области.
В жесткопластической неоднородной модели взаимодействия пород и крепи учитываются разрушение и, следовательно, изменение свойств пород в некоторой области вокруг выработки в процессе взаимодействия массива с крепью. При этом порода в зоне разрушения принимается как идеально сыпучая среда или обладающая некоторым сцеплением.
Жестколластическая модель массива пород позволяет изучать его способность к пластическим (необратимым) деформациям, величина которых значительно превышает упругие деформации, вследствие чего последние во внимание не принимаются. В жесткопластической среде поэтому различают пластические и жесткие (недеформируемые) области. Основное смещение пород происходит в зоне смещения под действием массы смещающихся пород за счет их неупругих деформаций. Упругие деформации массива за пределами зоны смещений влияния на выработку практически не оказывают, поэтому здесь он рассматривается как жесткий. Жесткопластическая модель наиболее применима для сыпучих и сильнотрещиноватых горных пород.
Экспериментально доказано, что механизм пластической деформации связан со сдвигами материала по некоторым площадкам. Поэтому структурную схему жесткопластической среды можно представить в виде элемента трения (рис. 13).
Из этой схемы непосредственно следует условие скольжения (условие Кулона – Мора):
τ = K +σнtgφ,
где K – сцепление (сопротивление сдвигу, не зависящее от величины нормального давления); σн – нормальные напряжения на площадке скольжения; φ – угол внутреннего трения. Если сдвигающее усилие меньше значения τ, то никаких деформаций не происходит. Условие называют также условием предельного состояния.
Из диаграммы (рис. 13, а) можно представить условие предельного состояния (условие Кулона – Мора) в главных напряжениях:
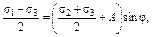
где А = К ctg φ, при σ3 = 0 из этого уравнения получаем выражение для предела прочности пород при одноосном сжатии:

После достижения предельного состояния пластическая деформация становится неопределенной. На основе жесткопластической модели построены гипотеза свода обрушения, гипотеза опускающегося столбца пород и др.
Раздельно-блочная модель относится к дискретным средам. Механика дискретных сред применительно к подземным сооружениям и горным выработкам в настоящее время практически не разработана.
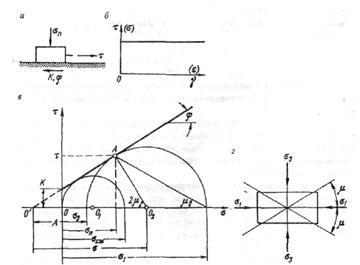
Рис. 13. Структурная схема (а), диаграмма напряжений (б) жесткопластической модели; диаграмма наибольших кругов напряжений (в)
и ориентировка площадок скольжения относительно главных напряжений
(г) в пластической среде
Реальный массив горных пород разбит трещинами. В ряде случаев трещиноватостm не только влияет на механические характеристики пород в массиве, но и, расчленяя массив на структурные элементы – блоки, придает новое качество массиву, деформации которого оказываются связанными с взаимным смещением блоков, а напряженное состояние – с напряжением на их контактах. Поведение такой среды носит вероятностный характер.
 2014-02-17
2014-02-17 6168
6168








