Электропроводность растворов электролитов

При наложении разности потенциалов к раствору, ионы находившиеся в непрерывном хаотическом тепловом движении, приобретают направленное движение от одного полюса к другому: катионы и анионы движутся в противоположных направлениях – возникает электрический ток. Так как растворы электролитов переносят электричество за счет движения ионов, их относят к проводникам второго рода.

Количественной характеристикой способности системы проводить электрический ток является электропроводность. Единицей электропроводности растворов электролитов служит удельная электропроводность :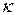

, []

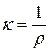где 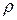– удельное сопротивление: ;

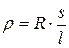где 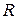– общее сопротивление проводника, ;

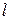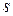, – длина, 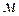и поперечное сечение проводника, .

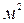Удельная электропроводность – это электрическая проводимость объема раствора, заключенного между двумя параллельными электродами площадью по 1 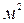, расположенными на расстоянии 1 .

Удельная электропроводность зависит от

– концентрации электролита;

– вязкости и диэлектрической проницаемости растворителя;

– температуры;

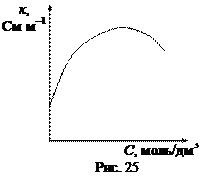– скорости движения ионов, которая определяется величиной заряда иона и его радиуса с учетом гидратации.

При увеличении концентрации электролита удельная электропроводность сначала увеличивается, а затем уменьшается (рис. 25). Такая зависимость характерна как для сильных, так и для слабых электролитов. В случае слабых электролитов падение удельной электропроводности в области высоких концентраций объясняют уменьшением степени диссоциации, а сильных – электростатическим взаимодействием между ионами в растворе.

Молярная электропроводность 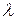– это удельная электропроводность объема раствора электролита, содержащего 1 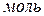растворенного вещества:

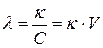, [], (183)

где – разведение (объем раствора, в котором содержится 1 моль электролита).

Если молярная концентрация 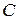выражена в 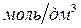, то:

; [].

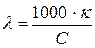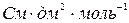где 1000 – коэффициент перевода концентрации из 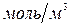в .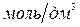

С ростом разбавления (уменьшением концентрации) электролита молярная электропроводность возрастает, что объясняют уменьшением электростатического взаимодействия ионов (рис. 26). На рис. 26 кривая I соответствует сильному электролиту, кривая II – слабому. Каждая кривая отсекает на оси ординат отрезок, характеризующий предельную молярную электропроводность 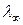– т.е. 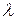при бесконечном разбавлении раствора (при ).

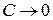С повышением температуры электропроводность растворов электролитов увеличивается. Это объясняют понижением вязкости раствора и, как следствие, увеличением скорости перемещения ионов, а для слабых электролитов еще и увеличением степени диссоциации.

В условиях предельного разбавления выполняется закон независимого движения ионов – закон Кольрауша, согласно которому предельная молярная электропроводность 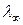раствора электролита равна сумме молярных электропроводностей (подвижностей) катиона 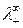и аниона 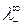при бесконечном разбавлении:

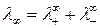. (184)

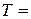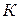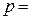Предельные подвижности ионов определены экспериментально в стандартных условиях (298 , 1 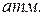) и приведены в справочной литературе.

Подвижность иона характеризует количество электричества, которое он переносит и определяется абсолютной скоростью его движения (или абсолютной подвижностью – т.е. скоростью движения при напряженности электрического поля 1 ).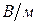

Абсолютные скорости движения большинства ионов равны 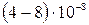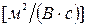. Исключение составляют только ионы гидроксония 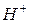и гидроксил–ионы 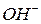, для которых 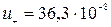и .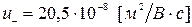

Так как абсолютные скорости движения катионов и анионов неодинаковы, то доля электричества, переносимого отдельными ионами может различаться. Для характеристики количества электричества, переносимого данным видом ионов применяют числа переноса. Число переноса – это отношение количества электричества 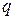, перенесенного данным видом ионов к общему количеству электричества, перенесенного раствором электролита.

; ,

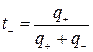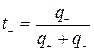где 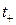, 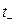– числа переноса катионов и анионов, соответственно.

Числа переноса катионов 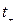и анионов 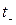можно выразить через электропроводности:

; .

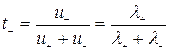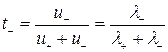Таким образом, числа переноса ионов – есть относительные скорости их движения или их относительные подвижности.

Сумма чисел переноса катионов и анионов

.

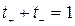Числа переноса ионов электролитов определены и приведены в справочной литературе.

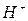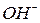Поскольку большинство катионов и анионов (кроме и ) характеризуются сопоставимыми скоростями движения в растворах, то числа переноса ионов большинства бинарных электролитов не сильно отличаются от 0,5. Несмотря на различия в числах переноса катионов и анионов нарушения закона электронейтральности не происходит.

Влияние межионного взаимодействия на электропроводность раствора отражает коэффициент электропроводности 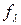, зависящий от концентрации электролита, вязкости растворителя, температуры:

,

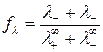А взаимосвязь 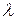с 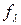и степенью диссоциации 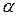выражает уравнение:

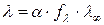. (185)

Для растворов слабых электролитов межионным взаимодействием можно пренебречь, тогда 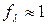, тогда

.

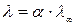Откуда следует, что

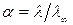. (186)

Уравнение Аррениуса (186) лежит в основе экспериментального метода определения степени и константы диссоциации слабого электролита по электропроводности раствора. Экспериментально определив 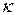для раствора известной концентрации, рассчитывают 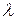. На основе справочных данных по уравнению Кольрауша вычисляют 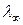, затем 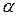по уравнению (186) и константу диссоциации 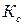по уравнению Оствальда (181).

Из закона разбавления Оствальда (181) и уравнения Аррениуса (186), получим:

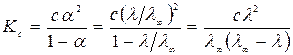. (187)

Для сильных электролитов 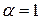, тогда из (185) получим

.

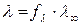Следовательно, 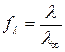. (188)