Объем тела

Если f (x,y) > 0 в области интегрирования R, то объем цилиндрического тела с основанием R, ограниченного сверху поверхностью z = f (x,y), выражается формулой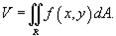

В случае, когда R является областью типа I, ограниченной линиями 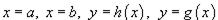, объем тела равен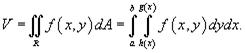

Для области R типа II, ограниченной графиками функций 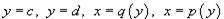, объем соответственно равен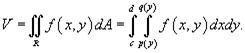

сли в области R выполняется неравенство 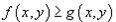, то объем цилиндрического тела между поверхностями z₁ = f (x,y) и z2 = g (x,y) с основанием R равен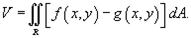

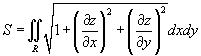3. Площадь поверхности Предположим, что поверхность задана функцией z = f (x,y), имеющей область определения R. Тогда площадь такой поверхности над областью z определяется формулой

при условии, что частные производные 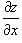и 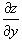непрерывны всюду в области R.

Физические приложения двойных интегралов