Анализ вариации зависимой переменной

Цель регрессионного анализа состоит в объяснении поведения зависимой переменной у.

Пусть на основе выборочных наблюдений построено уравнение регрессии 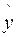, тогда значение зависимой переменной у в каждом наблюдении можно разложить на две составляющие 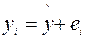, где остаток e_i есть та часть зависимой переменной у, которую невозможно объяснить с помощью уравнения регрессии.

Разброс значений зависимой переменной характеризуется выборочной дисперсией 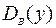. Разложим дисперсию :

.

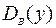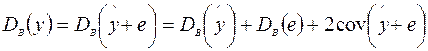Поскольку ,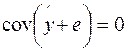

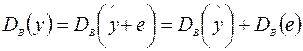
Замечание. Такое разложение дисперсии верно лишь в том случае, когда константа а включена в уравнение регрессии.

Таким образом, дисперсия 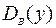разложена на две части:

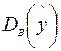— часть, объясненную регрессионным уравнением;

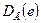— необъясненную часть.

Коэффициентом детерминации R² называется отношение

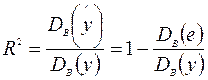
причем 0 £ R ² £ 1, характеризующее долю вариации (разброса) зависимой переменной, объясненную с помощью уравнения регрессии.

Для вычисления коэффициента детерминации 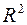можно воспользоваться функцией Excel КВПИРСОН(изв_значение_y; изв_значение_x).

Отношение 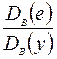представляет собой долю необъясненной дисперсии.

Если R ² = 1, то подгонка точная: 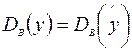, , , 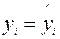i = 1,…, n,

т.е. все точки наблюдения лежат на регрессионной прямой.

Если R ² = 0, то регрессия ничего не дает: 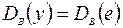, , 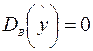, 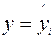i = 1,…, n,

т.е. переменная х не улучшает качества предсказания у по сравнению с горизонтальной прямой.

Чем ближе к единице R ², тем лучше качество подгонки, т.е. 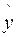более точно аппроксимирует y.

Замечание. Вычисление R ²корректно, есликонстанта а включена в уравнение регрессии.

Коэффициент детерминации не указывает причины и следствия. Он просто является математическим выражением взаимосвязи между переменными и показывает степень их взаимосвязанных изменений.

Еще одним показателем взаимосвязи является коэффициент корреляции Пирсона, который вычисляется по формул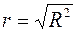е , где 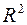¾ коэффициент детерминации.

Для вычисления коэффициента корреляции Пирсона 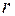можно воспользоваться функциями ПИРСОН(массив 1; массив 2) или КОРРЕЛ(массив 1; массив 2), где Массив 1 и 2 ¾ это значения x и y, причем порядок роли не играет. (В Excel 2007 этой функции нет и вместо нее нужно использовать КОРРЕЛ(массив1; массив2)).

Коэффициент корреляции Пирсона содержит информацию о поведении у с ростом х. Знак коэффициента Пирсона совпадает со знаком коэффициента b. Чем ближе r к 1, тем ближе связь между х и у к линейной. При 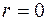линейной взаимосвязи между х и у не существует, но, возможно, есть другая зависимость.