2015-01-07
715
Элементы математической статистики
Задание 12.1 Из генеральной совокупности извлечена выборка. Данные наблюдений сведены в группы и представлены в виде дискретного ряда, где первая строка – середины частичных интервалов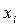 
, вторая строка –соответствующие им частоты 
.
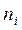Требуется провести статистическую обработку экспериментальных данных по следующей схеме:
а) построить выборочную (эмпирическую) функцию распределения;
б) построить гистограмму и полигон относительных частот;
в) найти числовые характеристики выборки: выборочную среднюю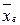 
, выборочное среднее квадратическое отклонение 
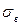и исправленное среднее квадратическое отклонение 
;
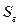г) сделать предварительный выбор закона распределения по виду гистограммы и полигона относительных частот;
д) проверить с помощью критерия Пирсона гипотезу о нормальном законе распределения генеральной совокупности при уровне значимости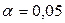 
;
е) в случае принятия гипотезы найти с надёжностью (доверительной вероятностью)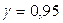 
интервальные оценки параметров нормального распределения.
12.1.1
| xi | ||||||
| ni |
12.1.2
| xi | ||||||
| ni |
12.1.3
| xi | ||||||
| ni |
12.1.4
| xi | ||||||
| ni |
12.1.5
| xi | ||||||
| ni |
12.1.6
| xi | ||||||
| ni |
12.1.7
| xi | ||||||
| ni |
12.1.8
| xi | ||||||
| ni |
12.1.9
| xi | ||||||
| ni |
12.1.10
| xi | ||||||
| ni |
Задание 12.2 Данные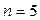 
наблюдений приведены в таблице.
Требуется:
а) найти выборочный коэффициент корреляции;
б) записать выборочные уравнения прямой Y на X и X на Y;
в) построить графики линий регрессии на одном чертеже.
12.2.1
| xi | ||||||
| yi |
12.2.2
| xi | ||||||
| yi |
12.2.3
| xi | ||||||
| yi |
12.2.4
| xi | ||||||
| yi |
12.2.5
| xi | ||||||
| yi |
12.2.6
| xi | ||||||
| yi |
12.2.7
| xi | ||||||
| yi |
12.2.8
| xi | ||||||
| yi |
12.2.9
| xi | ||||||
| yi |
12.2.10
| xi | ||||||
| yi |
