4.3.1. При расчетах цепей переменного синусоидального тока используются те же законы и методы, что и при расчете цепей постоянного тока, но все электрические величины – токи, ЭДС, напряжения, сопротивления, - должны быть записаны в комплексной форме. В связи с необходимостью выполнения при расчетах различных математических действий: сложения/вычитания, умножения/деления,- рекомендуется использовать как алгебраическую, так и показательную формы записи комплексных чисел.
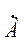 = а + jb =A e
= а + jb =A e 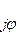 , (4.3.1)
, (4.3.1)
где А – модуль величины,
а и b – ее действительная и мнимая части.
А = 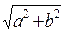 (4.3.2)
(4.3.2)
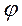 = arc tg b/a (4.3.3)
= arc tg b/a (4.3.3)
для перехода от показательной формы записи к алгебраической нужно использовать выражения
а = А cos 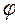 (4.3.4)
(4.3.4)
b = A sin 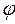 (4.3.5)
(4.3.5)
4.3.2.При составлении расчетной схемы необходимо:
а) заменить полные сопротивления составляющими их элементами: активными сопротивлениями, индуктивностями и емкостями;
б) источники тока источниками ЭДС.
Ветви с источниками тока, равными нулю, на схему не наносятся.
4.3.3. Для определения линейной частоты f следует использовать связывающее ее с угловой частотой 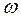 соотношение
соотношение
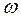 = 2пf (4.3.6)
= 2пf (4.3.6)
4.3.4. Расчет токов в ветвях следует вести в изложенной ниже последовательности
а) Вычислить сопротивления реактивных элементов
ХL = 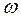 L (Ом) (4.3.7)
L (Ом) (4.3.7)
ХC = 1/ 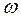 C (Ом) (4.3.8)
C (Ом) (4.3.8)
б) Записать в комплексной форме заданные величины, используя приведенные в п. 4.3.1 формулы.
Например:
- ЭДС дана в виде Е = 100 В; 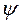 = 650; тогда показательная форма этой ЭДС имеет вид
= 650; тогда показательная форма этой ЭДС имеет вид
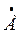 = 100 е j65
= 100 е j65 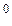 ,
,
а перевод ее в алгебраическую форму выполняется по (4) и (5);
- сопротивление ветви состоит из резистора R, индуктивного ХL и емкостного ХС сопротивлений
R = 3 Ом; ХL = 9 Ом; ХС = 5 Ом. Тогда удобней первоначальную запись комплексного сопротивления выполнить в алгебраической форме
Z = R + j (ХL – ХС) = 3 + j (9 – 5) = 3 + j 4
c последующим ее переводом в показательную форму по (4.3.1) – (4.3.3).
Результаты расчетов занести в таблицу 6.
Таблица 6 - Результаты расчета заданных величин и параметров схемы
в алгебраической и показательной форме.
| Величина, параметр | Алгебраическая форма | Показательная форма |
в) Составить контурные уравнения для своей расчетной схемы замещения, используя выражение ЭДС и сопротивлений комплексными числами. Для упрощения операций умножения и деления при составлении уравнений предпочтительней использовать показательную форму комплексов.
г) Решить полученную систему уравнений и, найдя контурные токи, определить токи в ветвях, напряжения на каждом комплексном сопротивлении и их элементах. Результаты расчетов занести в таблицу 7. Количество строк в таблице зависит от числа найденных величин.
Таблица 7 - Результаты расчета токов и напряжений.
| Искомая величина | Алгебраическая форма | Показательная форма | Действующее значение |
Правильность расчетов может быть проверена по уравнениям, составленным по первому закону Кирхгофа.
4.3.5. Найти комплекс мощности S источника питания как произведение комплекса ЭДС источника на сопряженный комплекс тока 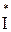 , даваемого этим источником.
, даваемого этим источником.
S = 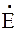
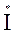 ,(4.3.9) где сопряженный комплекс тока равен комплексу тока, у которого знак мнимой части изменен на противоположный. Например,
,(4.3.9) где сопряженный комплекс тока равен комплексу тока, у которого знак мнимой части изменен на противоположный. Например, 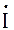 = 3 + j4, тогда сопряженный комплекс в алгебраической форме
= 3 + j4, тогда сопряженный комплекс в алгебраической форме 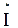 = 3 - j4.
= 3 - j4.
При использовании показательной формы необходимо в сопряженном комплексе изменить знак показателя.
Заменой комплекса тока на его сопряженный комплекс учитывается угол сдвига фаз между ЭДС и током для источников питания (напряжением и током для приемников).
Полная мощность равна модулю комплекса мощности, или
S = Е I, (4.3.10)
а действительная и мнимая части комплекса мощности соответствуют активной и реактивной мощности, или
Р = S cos 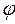 ; (4.3.11)
; (4.3.11)
Q = S sin 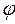 , (4.3.12)
, (4.3.12)
где 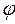 - угол сдвига по фазе между ЭДС и током источника питания.
- угол сдвига по фазе между ЭДС и током источника питания.
Суммарную мощность всех действующих в цепи источников питания проще найти, записав комплексы мощностей каждого источника в алгебраической форме.
Результаты определения мощностей показать в таблице, форму которой составить самостоятельно.
4.3.6. Для составления баланса активных мощностей следует определить активную мощность, потребляемую активными сопротивлениями (резисторами) n-й ветви цепи
Pпотр. = 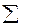 I n
I n 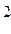 Rn, (4.3.13)
Rn, (4.3.13)
где In – действующее значение тока ветви, А;
Rn – активное сопротивление ветви, Ом.
Потребляемая цепью активная мощность должна быть равна активной мощности, отдаваемой всеми источниками питания (см. п. 4.3.5).
4.3.7. Уравнения мгновенных значений заданных ЭДС имеют вид
е = Еm sin (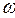 t +
t + 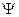 ) (4.3.14)
) (4.3.14)
где 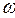 - угловая частота,
- угловая частота, 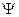 - начальная фаза каждой ЭДС (см. задание).
- начальная фаза каждой ЭДС (см. задание).
4.3.8. Построение векторной диаграммы.
Для данной на рис.12 схемы выполнен расчет, результаты которого отражены в общем виде в таблице 7а, где действительные части комплексов токов 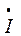 и напряжений
и напряжений 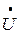 обозначены I' и U', а мнимые I" и U".
обозначены I' и U', а мнимые I" и U".
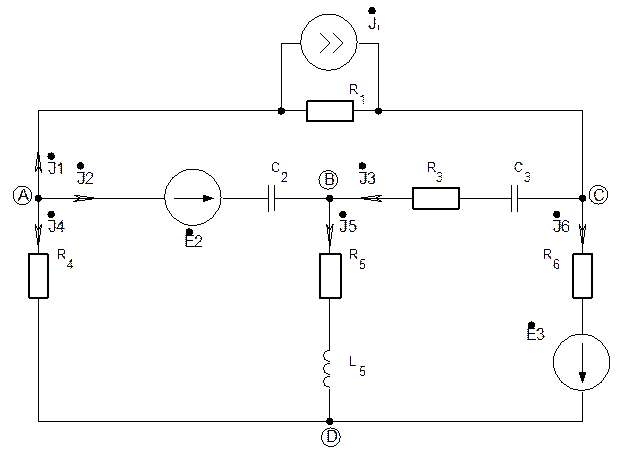
Рис. 12. Схема однофазной цепи
Таблица 7а - Результаты расчета токов и напряжений
| Искомая величина | Алгебраическая форма | Показательная форма | Действующее значение | |
| Токи ветвей, А | 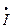 1 1 | I'1 + jI"1 | I1 e 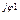 | I1 |
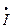 2 2 | I'2 + jI"2 | I2 e 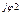 | I2 | |
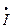 3 3 | I'3 + jI"3 | I3 e 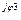 | I3 | |
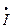 4 4 | I'4 + jI"4 | I4 e 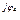 | I4 | |
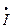 5 5 | I'5 + jI"5 | I5 e 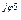 | I5 | |
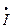 6 6 | I'6 + jI"6 | I6 e 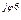 | I6 |
Продолжение таблицы 7а
| Напряжения на сопротивлениях, В |  1 = 1 =  R1 R1 | U'1 + j U"1 | U1 e 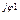 | U1 |
 2 = 2 =  C2 C2 | U'2+ jU"2 | U2 e 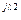 | U2 | |
 3 3 | U'3 + jU"3 | U3 e 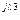 | U3 | |
 R3 R3 | U'R3 + jU"R3 | UR3 e 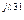 | UR3 | |
 C3 C3 | U'C3 + jU"C3 | UC3 e 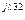 | UC3 | |
 4 = 4 =  R4 R4 | U'4 + jU"4 | U4 e 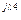 | U4 | |
 5 5 | U'5 + jU"5 | U5 e 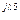 | U5 | |
 R5 R5 | U'R5 + jU"R5 | UR5 e 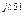 | UR5 | |
 5 5 | U'L5 + jU"L5 | UL5 e 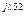 | UL5 | |
 6 = 6 =  R6 R6 | U'6 + jU"6 | U6 e 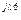 | U6 |
На рис. 13 дана векторная диаграмма токов и напряжений в цепи, при построении которой соблюдалась следующая последовательность:
1. Строятся оси комплексной плоскости: действительных величин (+1) – горизонтально, мнимых величин (j) – вертикально.
2. Исходя из значений модулей токов и напряжений и размеров поля листа, отведенного для построения диаграммы, выбираются масштабы тока mI и напряжения mU. Например, при использовании формата А4 (размеры 210х297 мм) при наибольших модулях тока 40 А и напряжения U = 500 В приняты масштабы: mI = 5 А/см, mU = 50 В/см.
3. С учетом принятых масштабов mI и mU определяется длина каждого вектора, если диаграмма строится с использованием показательной формы его записи; при использовании алгебраической формы находятся длины проекций векторов на оси действительных и мнимых величин, т.е. длины действительной и мнимой частей комплекса.
Например, для записанных в комплексной форме тока, I = 40 е 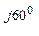 = 20 + j34,6 и напряжения U = 500 е
= 20 + j34,6 и напряжения U = 500 е 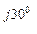 = 433 + j 250 В:
= 433 + j 250 В:
- длина вектора тока /I / = 40 А/ 5 А/см = 8 см; длина его действительной части I = 20 А / 5 А/см = 4 см, длина его мнимой части I = 34,6 А / 5 А/см = 6,9 см;
- длина вектора напряжения / U / = 500 В / 50 В/см = 10 см; длина его действи-
тельной части U = 433 В / 50 В/см = 8,66 см; длина его мнимой части U =
= 250 В / 50 В/см = 5 см.
Результаты определения длин векторов, их действительных и мнимых частей нужно отразить в таблице 7б.
Таблица 7б - Длины векторов тока и напряжения, их действительных и
мнимых частей
| Величина | Масштаб, 1/см | Длина вектора, см | Длина действительной части, см | Длина мнимой части, см | |
| Токи ветвей | 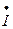 1 1 | mI= 5 А/см | |||
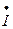 2 2 | |||||
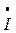 3 3 | |||||
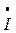 4 4 | |||||
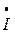 5 5 | |||||
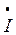 6 6 | |||||
| ЭДС и напряжения | 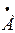 1 1 | mU=50 В/см | |||
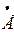 2 2 | |||||
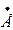 6 6 | |||||
 1= 1=  R1 R1 | |||||
 R1 R1 | |||||
 2 = 2 =  C2 C2 | |||||
 3 3 | |||||
 R3 R3 |
Продолжение таблицы 7б
| ЭДС и напряжения |  C3 C3 | mU=50 В/см | |||
 4 = 4 =  R4 R4 | |||||
 5 5 | |||||
 R5 R5 | |||||
 L5 L5 | |||||
 6 = 6 =  R6 R6 |
4. На комплексной плоскости строятся вектора всех ЭДС, напряжений и токов. Для их построения можно использовать обе формы записи комплексов ЭДС, напряжений и токов.
Например, вектор тока 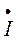 , комплекс которого использован в п. 3 в качестве примера, строится по показательной форме следующим образом: от оси (+1) под углом 30
, комплекс которого использован в п. 3 в качестве примера, строится по показательной форме следующим образом: от оси (+1) под углом 30 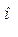 , т.е. против часовой стрелки, откладывается отрезок длиной 8 см; по алгебраической форме его можно построить, отложив по оси (+1) отрезок длиной 4 см, а по оси (j) отрезок длиной 6,96 см, концы этих отрезков являются координатами конца вектора
, т.е. против часовой стрелки, откладывается отрезок длиной 8 см; по алгебраической форме его можно построить, отложив по оси (+1) отрезок длиной 4 см, а по оси (j) отрезок длиной 6,96 см, концы этих отрезков являются координатами конца вектора 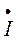 .
.
На векторной диаграмме (рис. 13) использованы оба способа построения векторов: векторы токов построены по показательной форме записи, а векторы ЭДС и напряжений по алгебраической.
5. Правильность расчета цепи и построения векторной диаграммы проверяется по взаимному расположению векторов, а также их сложением. Так, например,
для используемой в качестве примера схемы (рис. 12):
- векторы токов 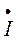 1,
1, 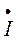 4 и
4 и 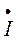 6 и напряжений
6 и напряжений  1,
1,  4 и
4 и  6 совпадают по фазе;
6 совпадают по фазе;
- вектор напряжения  R5 должен совпасть по фазе с вектором I5, а вектор
R5 должен совпасть по фазе с вектором I5, а вектор  L5 опережает вектор тока
L5 опережает вектор тока 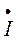 5 на 90
5 на 90 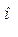 ;
;
- сумма токов узла В 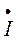 1 и
1 и 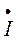 5 соответствии с первым законом Кирхгофа должна быть равна току
5 соответствии с первым законом Кирхгофа должна быть равна току 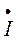 6;
6;
- по второму закону Кирхгофа для контура 111 при сложении векторов напряжений  3,
3,  6 и
6 и  5 должен получиться вектор
5 должен получиться вектор 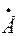 6.
6.
Таким образом может быть выполнена проверка для всех ветвей, узлов и контуров.
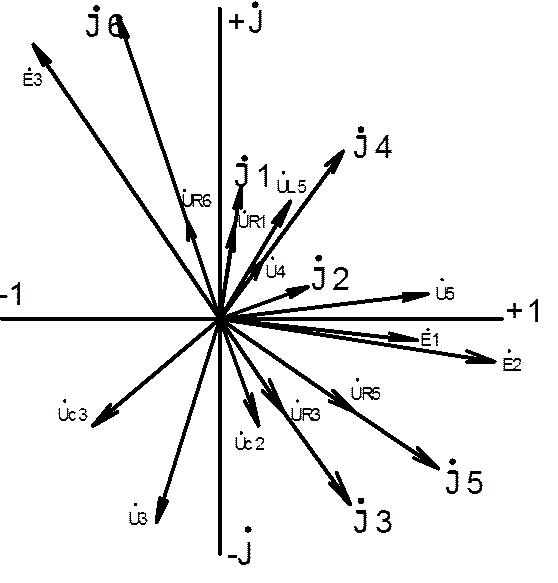
Рис. 13. Векторная диаграмма токов и напряжений для схемы на рис. 12.
 2015-02-27
2015-02-27 3068
3068
