Свободная частица – частица, движущаяся в отсутствие внешних полей. Т.к. на свободную частицу (пусть она движется вдоль оси x) силы не действуют, то потенциальная энергия частицы 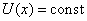 и ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией.
и ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией.
В таком случае уравнение Шредингера для стационарных состояний примет вид:
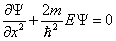 . . | (5.1.1) |
Прямой подстановкой можно убедиться в том, что частным решением уравнения (5.1.1) является функция 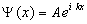 , где
, где 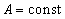 и
и 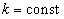 , с собственным значением энергии:
, с собственным значением энергии:
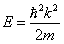 . . | (5.1.2) |
Функция 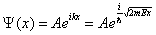 представляет собой только координатную часть волновой функции
представляет собой только координатную часть волновой функции 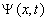 .
.
Зависящую от времени волновую функцию можно представить в виде:
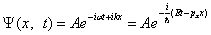 , , | (5.1.3) |
где 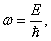
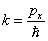 .
.
Функция (5.1.3) представляет собой плоскую монохроматическую волну де Бройля.
Из выражения (5.1.2) следует, что зависимость энергии от импульса
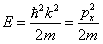 | (5.1.4) |
оказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые значения, т.е. ее энергетический спектр является непрерывным.
Таким образом, свободная частица описывается плоской монохроматической волной де Бройля. Этому способствует не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространства:
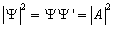 ,
,
т.е. все положения свободной частицы являются равновероятностными.
Проведем качественный анализ решений уравнения Шредингера применительно к частице, находящейся в потенциальной яме с бесконечно высокими «стенками».
Такая яма описывается потенциальной энергией U (x) следующего вида:
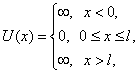
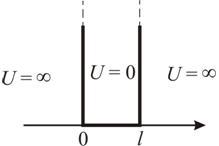
где l – ширина ямы, а энергия отсчитывается от ее дна (рис. 5.1).
 х
х
Рис. 5.1
Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде:
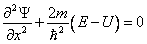 . . | (5.2.1) |
По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы ямы, поэтому вероятность ее обнаружения за пределами ямы равна нулю. На границах ямы волновая функция также должна обращаться в нуль. Следовательно, граничные условия в таком случае имеют вид:
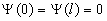 . . | (5.2.2) |
В пределах ямы (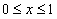 ) уравнение Шредингера (5.2.1) сводится к уравнению
) уравнение Шредингера (5.2.1) сводится к уравнению
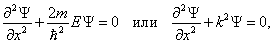 | (5.2.3) |
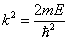 | (5.2.4) |
Общее решение дифференциального уравнения:
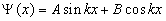 .
.
А т.к. по (5.2.2) 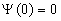 , то B = 0. Тогда
, то B = 0. Тогда
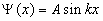 , , | (5.2.5) |
уравнение 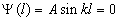 выполняется только при
выполняется только при 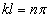 , где n – целые числа, т.е. необходимо, чтобы
, где n – целые числа, т.е. необходимо, чтобы
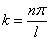 . . | (5.2.6) |
Из выражений (5.2.4) и (5.2.6) следует, что энергия частицы зависит от n:
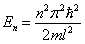 , , | (5.2.7) |
где n = 1, 2, 3….
Т.е. стационарное уравнение Шредингера, описывающее движение частицы в потенциальной яме с бесконечно высокими стенками, удовлетворяется только при собственных значениях En, зависящих от целого числа n. Следовательно, энергия En частицы в потенциальной яме с бесконечно высокими стенками принимает лишь определенные дискретные значения, т.е. квантуется. Квантовые значения энергии En называются уровнями энергии, а число п, определяющее энергетические уровни – главным квантовым числом.
Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими стенками может находиться только на определенном энергетическом уровне En, или, как говорят, частица находится в квантовом состоянии п.
Подставив k в (5.2.5), из (5.2.6) найдем собственные функции:
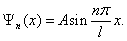
Постоянную интегрирования А найдем из условия нормировки (4.3.3), которое для данного случая запишется в виде:
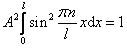
В результате интегрирования получим 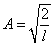 , а собственные функции будут иметь вид:
, а собственные функции будут иметь вид:
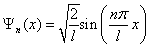 . . | (5.2.8) |
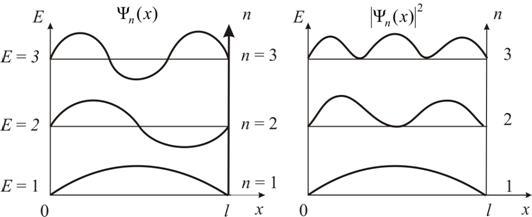
| а | б |
Рис. 5.2
Графики собственных функций (5.2.8), соответствующие уровням энергии (5.2.7) при п = 1, 2, 3, приведены на рис. 5.2, а. На рис. 5.2, б изображена плотность вероятности обнаружения частицы на различных расстояниях от «стенок» ямы: 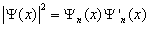 для п = 1, 2, 3. Из рисунка следует, что, например, в квантовом состоянии с п = 2 частица не может находиться в центре ямы, в то время как одинаково может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны.
для п = 1, 2, 3. Из рисунка следует, что, например, в квантовом состоянии с п = 2 частица не может находиться в центре ямы, в то время как одинаково может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны.
Из выражения 5.2.7 следует, что энергетический интервал между двумя соседними уровнями равен:
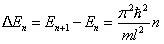 . . | (5.2.9) |
Например, для электрона при размерах ямы 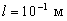 (свободные электроны в металле)
(свободные электроны в металле) 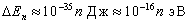 , т.е. энергетические уровни расположены столь тесно, что спектр можно считать практически непрерывным. Если же размеры ямы соизмеримы с размерами стенки (
, т.е. энергетические уровни расположены столь тесно, что спектр можно считать практически непрерывным. Если же размеры ямы соизмеримы с размерами стенки (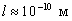 ), то для электрона
), то для электрона 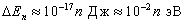 , т.е. получаются явно дискретные значения энергии (линейчатый спектр). Таким образом, применение уравнения Шредингера к частице в потенциальной яме с бесконечно высокими стенками приводит к квантовым значениям энергии и координат, в то время как классическая механика на энергию этой частицы лишних ограничений не накладывает.
, т.е. получаются явно дискретные значения энергии (линейчатый спектр). Таким образом, применение уравнения Шредингера к частице в потенциальной яме с бесконечно высокими стенками приводит к квантовым значениям энергии и координат, в то время как классическая механика на энергию этой частицы лишних ограничений не накладывает.
Кроме того, квантово-механическое рассмотрение этой задачи приводит к выводу, что частица в потенциальной яме с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная 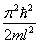 . Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотношения неопределенностей. Неопределенность координаты Δ x частицы в яме шириной l равна: Δ x = l. Тогда согласно соотношению неопределенностей, импульс не может иметь точное, в данном случае нулевое, значение.
. Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотношения неопределенностей. Неопределенность координаты Δ x частицы в яме шириной l равна: Δ x = l. Тогда согласно соотношению неопределенностей, импульс не может иметь точное, в данном случае нулевое, значение.
Неопределенность импульса:
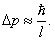 Такому разбросу значений импульса соответствует кинетическая энергия
Такому разбросу значений импульса соответствует кинетическая энергия 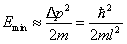 . Все остальные уровни имеют энергию, превышающую это значение.
. Все остальные уровни имеют энергию, превышающую это значение.
Из функций (5.2.1) и (5.2.7) следует, что при больших квантовых числах 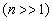
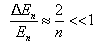 , т.е. соседние уровни расположены тесно: тем теснее, чем больше п. Если п очень велико, то можно говорить о практически непрерывной последовательности уровней,и характерная особенность квантовых процессов – дискретность – сглаживается. Этот результат является частным случаем принципа соответствия Бора, согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики.
, т.е. соседние уровни расположены тесно: тем теснее, чем больше п. Если п очень велико, то можно говорить о практически непрерывной последовательности уровней,и характерная особенность квантовых процессов – дискретность – сглаживается. Этот результат является частным случаем принципа соответствия Бора, согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики.
Более общая трактовка принципа соответствия: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а включает в себя классическую теорию, указывая границы ее применимости, причем в определенных предельных условиях новая теория переходит в старую.
Модель Резерфорда. Постулаты Бора. Расчет скорости движения и радиуса орбиты. Энергетические уровни и спектральные серии для атома водорода
Резерфорд и его сотрудники наблюдали прохождение α-частиц через тонкую золотую фольгу. Скорость α-частиц 107 м/с.
Экспериментальная установка позволяла наблюдать α-частицы, отклоненные золотой фольгой под разными углами.
В то время было известно, что α-частица имеет положительный заряд, равный +2 е.
Опыт осуществлялся по схеме, изображенной на рис. 6.3.
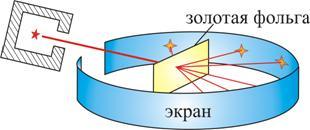
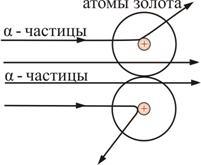
Рис. 6.3
Узкий пучок α-частиц испускался радиоактивным веществом и попадал на фольгу. Проходя через фольгу α-частицы отклонялись на различные углы. Рассеянные частицы ударялись об экран, покрытый ZnS, и вызываемые им вспышки света, сцинцилляции, наблюдались в микроскопе. Микроскоп и связанный с ним экран можно было вращать вокруг оси, проходящей через центр фольги. Т.е. можно было всегда измерить угол отклонения. Весь прибор помещался в вакуум, чтобы α-частицы не рассеивались при столкновении с молекулами воздуха.
В опыте обнаружилось, что некоторые α-частицы отклонялись на большие углы, до 180º. Резерфорд понял, что такое отклонение возможно лишь при встрече с положительно заряженной частицей большей массы. А малая вероятность отклонения на большие углы говорила, что эта положительная частица имеет малые размеры, порядка 10–14 м. Электроны, по мнению Резерфорда, движутся вокруг ядра.
В опыте обнаружилось, что некоторые α-частицы отклонялись на большие углы, до 180º. Резерфорд понял, что такое отклонение возможно лишь при встрече с положительно заряженной частицей большей массы. А малая вероятность отклонения на большие углы говорила, что эта положительная частица имеет малые размеры, порядка 10–14 м. Электроны, по мнению Резерфорда, движутся вокруг ядра.
Однако такая модель была в явном противоречии с классической электродинамикой, т.к. электрон, двигаясь по окружности, т.е. с нормальным ускорением, должен был излучать энергию, следовательно, замедлять скорость и падать на ядро. Таким образом, применение классической электродинамики к ядерной модели атома привело к полному противоречию с экспериментальными фактами.
Постулаты Бора.
Бор высказал предположения, которые были названы постулатами Бора.
· Первый постулат (постулат стационарных состояний): электроны движутся только по определенным (стационарным) орбитам. При этом, даже двигаясь с ускорением, они не излучают энергию.
· Второй постулат (правило частот): излучение и поглощение энергии в виде кванта света (hn) происходит лишь при переходе электрона из одного стационарного состояния в другое. Величина светового кванта равна разности энергий тех стационарных состояний, между которыми совершается скачок электрона: 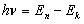 Уравнение движения электрона имеет вид:
Уравнение движения электрона имеет вид:
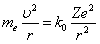 . (6.3.3) . (6.3.3) |
Из формулы (6.3.3) видно, что центробежная сила равна кулоновской силе, где 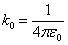 .
.
Подставим значение υ из (6.3.2) в (6.3.3) и получим выражение для радиусов стационарных орбит (рис.6.6,б):
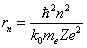 . . | (6.3.4) |
Радиус первой орбиты водородного атома называют боровским радиусом. При n =1, Z = 1 для водорода имеем:
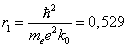 Å = 0,529·10–10 м.
Å = 0,529·10–10 м.
Внутренняя энергия атома слагается из кинетической энергии электрона (ядро неподвижно) и потенциальной энергией взаимодействия электрона с ядром:
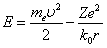 .
.
Из уравнения движения электрона следует, что 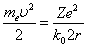 , т.е. кинетическая энергия равна потенциальной.
, т.е. кинетическая энергия равна потенциальной.
Тогда можно записать:
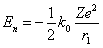
Подставим сюда выражение для радиуса первой орбиты и получим:
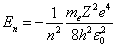 . . | (6.3.5) |
Здесь учтено, что постоянная Планка 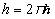 , т.е.
, т.е. 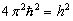 .
.
Для атома водорода при Z = 1 имеем:
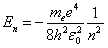 . . | (6.3.6) |
Из формулы (6.3.6) видно, что 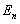 принимает только дискретные значения энергии, т.к. n = 1, 2, 3….
принимает только дискретные значения энергии, т.к. n = 1, 2, 3….
Схема энергетических уровней, определяемых уравнением (6.3.6) показана на рис. 6.1 и 6.7.
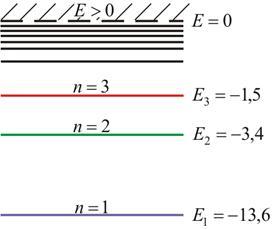
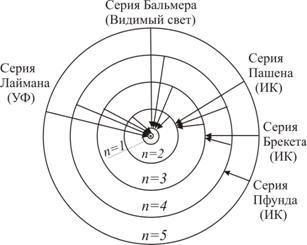
Рис. 6.7
При переходе электрона в атоме водорода из состояния n в состояние k излучается фотон с энергией:
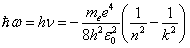 .
.
Частота излучения:
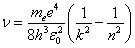 .
.
Получена обобщенная формула Бальмера, которая хорошо согласуется с экспериментом. Выражение перед скобками, как уже было сказано, носит название постоянной Ридберга:
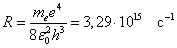 .
.
Стало ясно, что теория Бора является лишь переходным этапом на пути создания более общей и правильной теории. Такой теорией и явилась квантовая механика.
Решение уравнения Шредингера для атома водорода. Главное, орбитальное и магнитное квантовые числа. Спектр излучения атома водорода. Правила отбора.
В квантовой механике доказывается, что уравнению Шредингера удовлетворяют собственные функции 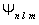 , определяемые набором трёх квантовых чисел: главного n, орбитального l и магнитного m.
, определяемые набором трёх квантовых чисел: главного n, орбитального l и магнитного m.
Главное квантовое числоn характеризует расстояние электрона от ядра – радиус орбиты.
Согласно (7.1.4) n определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения, начиная с единицы.
В атомной физике состояния электрона, соответствующие главному квантовому числу n, (n = 1, 2, 3, 4,) принято обозначать буквами K, L, M, N,
| n | ||||
| K | L | M | N |
Орбитальное квантовое число l = 0, 1, 2, n –1 характеризует эллиптичность орбиты электрона (рис. 7.3) и определяет момент импульса электрона 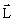 .
.
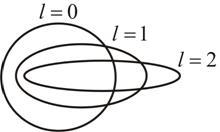
Рис. 7.3
Квадрат модуля функции 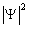 характеризует вероятность найти электрон в заданной точке. Область пространства, в которой высока вероятность обнаружить электрон (не менее 0,95), называют орбиталью. Основные типы орбиталей обозначают буквами s, p, d, f (от слов sharp, principal, diffuse, fundamental).
характеризует вероятность найти электрон в заданной точке. Область пространства, в которой высока вероятность обнаружить электрон (не менее 0,95), называют орбиталью. Основные типы орбиталей обозначают буквами s, p, d, f (от слов sharp, principal, diffuse, fundamental).
| l | ||||
| s | p | d | f |
Два типа орбиталей s (она одна), p (их три), по которым «размазан» электронный заряд, показаны на рис. 7.4.
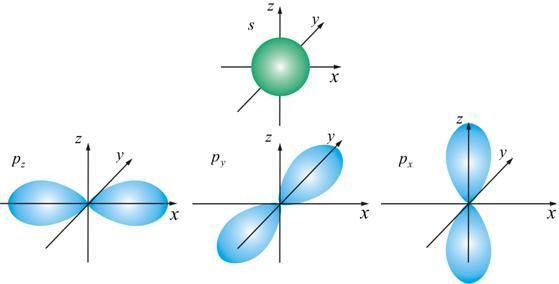
Рис. 7.4
Орбитали часто называют подоболочками оболочек, поскольку они характеризуют формы разных орбит, на которых можно обнаружить электроны, находящиеся в одной оболочке (при заданном квантовом числе n).
Решая последовательно задачу об электроне в прямоугольной потенциальной яме, мы доказали, что энергия и положение электрона квантуются, т.е. принимают дискретные значения.
Решая уравнения Шредингера для атома, можно получить выражения для энергии, момента импульса и других динамических переменных электрона без привлечения каких-либо постулатов.
Рассмотрим (без вывода) движение электрона в потенциальном поле 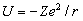 .
.
Обратимся вновь к стационарному уравнению Шредингера:
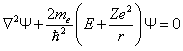 . . | (7.2.1) |
Так как электрическое поле – центрально-симметрично, то для решения этого уравнения воспользуемся сферической системой с координатами (r, θ, φ), которые связаны с декартовыми координатами, как это следует из рис. 7.5, соотношениями:
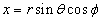 ;
;
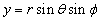 ;
;
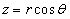 .
.
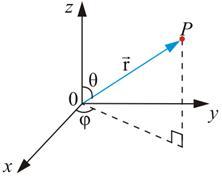
Рис. 7.5
Подставим в (7.2.1) выражение оператора Лапласа в сферических координатах и получим уравнение Шредингера в следующем виде:
 . . | (7.2.2) |
Уравнение (7.2.2) имеет решение при всех значениях полной энергии E > 0, что соответствует свободному электрону. При Е < 0 электрон находится в потенциальном поле ядра:
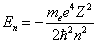 . . | (7.2.3) |
Таким образом, энергия принимает дискретные значения, т.е. квантуется (n = 1, 2, 3…).
Вывод такой же, как и в теории Бора, но в квантовой механике этот вывод получается как естественное следствие из уравнения Шредингера.
В квантовой механике широко используется понятие – оператор. Под оператором понимают правило, посредством которого одной функции φ сопоставляется другая функция f, т е. 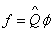 , где
, где 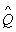 – символ обозначения оператора.
– символ обозначения оператора.
Используя оператор энергии, стационарное уравнение Шредингера можно записать в виде:
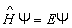 . . | (7.2.4) |
Это традиционный вид записи уравнения Шредингера, здесь 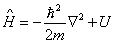 – оператор энергии – гальмитониан.
– оператор энергии – гальмитониан.
Воздействуя на волновую функцию Ψ, полученную при решении уравнения (7.2.2) оператором момента импульса (движение электрона вокруг ядра осуществляется по криволинейной траектории), можно получить выражение для момента импульса.
Для момента импульса в квантовой механике вводятся четыре оператора: оператор квадрата момента импульса 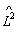 и три оператора проекций момента импульса на оси координат
и три оператора проекций момента импульса на оси координат 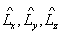 .
.
Оказалось, что одновременно определенные значения могут иметь лишь квадрат момента импульса и одна из проекций на координатные оси. Две другие проекции оказываются при этом совершенно неопределенными. Это означает, что «вектор» момента импульса не имеет определенного направления, и следовательно не может быть изображен, как в классической механике с помощью направленного отрезка, прямой.
Решение уравнения 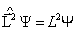 является очень трудным. Поэтому ограничимся только конечным результатом.
является очень трудным. Поэтому ограничимся только конечным результатом.
Собственное значение орбитального момента импульса L:
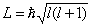 , , | (7.2.5) |
где l – орбитальное квантовое число (l = 0, 1, 2, n – 1).
Если обратиться к привычной нам модели атома, то n характеризует среднее расстояние электрона от ядра (радиус орбиты), l – эллиптичность орбиты.
Из выражения для L видно, что орбитальный момент импульса электрона в атоме тоже квантуется.
Основным состоянием электрона в атоме водорода является s -состояние. Если вычислить наиболее вероятное расстояние от ядра для электрона в s- состоянии, получим: 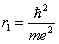 – это первый боровский радиус (в СИ
– это первый боровский радиус (в СИ 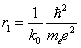 ).
).
Для других значений n получим выражения, соответствующие боровским орбитам.
Боровские орбиты электрона представляют собой геометрическое место точек, в которых с наибольшей вероятностью может быть обнаружен электрон.
По теории Бора, вероятность нахождения электрона при любых других значениях r, кроме r = 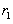 , равна нулю (рис. 7.6).
, равна нулю (рис. 7.6).
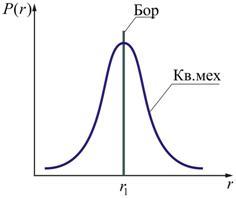
Рис. 7.6
Согласно квантовой механике эта вероятность достигает максимального значения лишь при r = 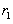 . Допускается нахождение электрона и на других расстояниях от ядра, но с меньшей вероятностью.
. Допускается нахождение электрона и на других расстояниях от ядра, но с меньшей вероятностью.
Спектры излучения атома водорода
В масштабе энергетические уровни атома водорода En в зависимости от главного квантового числа n, в соответствии с формулой (4.10).
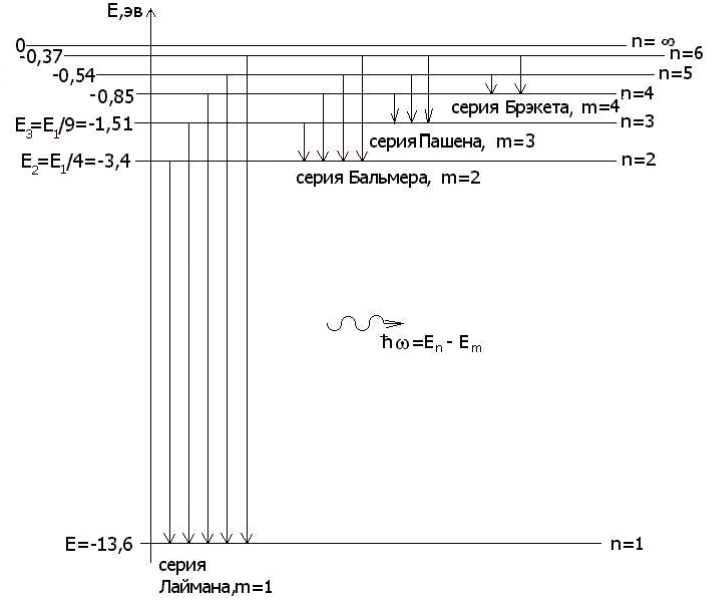
Рис. 4.2
Согласно второму постулату Бора (4.4.) энергия излученного фотона, 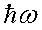 , равна разности энергий стационарных состояний, между которыми происходит квантовый переход:
, равна разности энергий стационарных состояний, между которыми происходит квантовый переход:
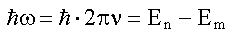 , в случае излучения n > m.
, в случае излучения n > m.
Подставляя сюда выражения для En и Em, (4.8) для частоты n, получим:
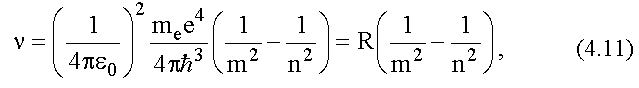
здесь
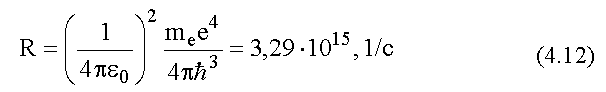
- постоянная Ридберга, она так названа в честь шведского физика И. Ридберга.
Так как λ = c/v, то для длины волны λ получим следующее выражение:
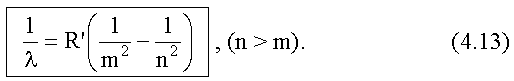
Здесь

- тоже называют постоянной Ридберга.
Из теории Бора следует, что спектр атома водорода имеет линейчатый характер, причем, наблюдаемые линии объединены в спектральные серии. Задается серия номером m уровня, на который происходит квантовый переход. Первые серии названы именами ученых-физиков:
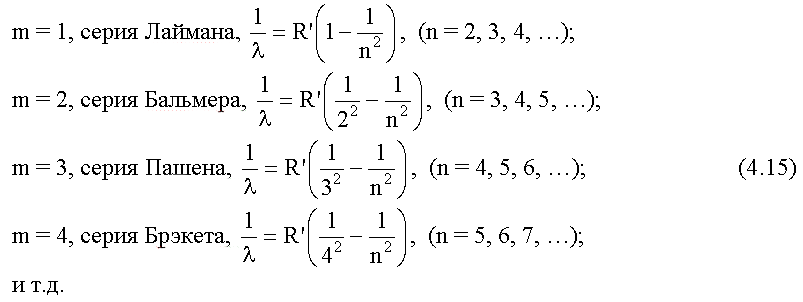
Спектры атома водорода были изучены экспериментально до создания Бором своей теории. Хорошее совпадение экспериментальных данных с выводами теории Бора для спектров атома водорода говорит в пользу этой теории.
Однако, попытки применить теорию Бора к более сложным атомам потерпели неудачу. В настоящее время теория атома Бора представляет исторический интерес как промежуточный этап к созданию более верной теории. Такая теория теперь существует - это квантовая механика.
Правилами отбора в спектроскопии называют ограничения и запрет на переходы между уровнями квантомеханической системы с поглощением или излучением фотона, наложенные законами сохранения и симметрией.
Опыт Штерна-Герлаха. Спин электрона и спиновое квантовое число
Идея опыта заключалась в измерении силы, действующей на атом в сильно неоднородном магнитном поле. Неоднородность магнитного поля должна быть такова, чтобы она сказывалась на расстояниях порядка размера атома. Только при этом можно было получить силу, действующую на каждый атом в отдельности.
Схема опыта изображена на рис. 7.9. В колбе с вакуумом, 10–5 мм рт. ст., нагревался серебряный шарик К, до температуры испарения.
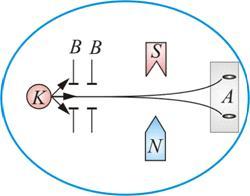

Рис. 7.9 Рис. 7.10
Атомы серебра летели с тепловой скоростью около 100 м/с через щелевые диафрагмы В и, проходя резко неоднородное магнитное поле, попадали на фотопластинку А.
Если бы момент импульса атома 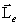 (и его магнитный момент
(и его магнитный момент 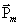 ) мог принимать произвольные ориентации в пространстве (т.е. в магнитном поле), то можно было ожидать непрерывного распределения попаданий атомов серебра на фотопластинку с большой плотностью попаданий в середине. Но на опыте были получены совершенно неожиданные результаты: на фотопластинке получились две резкие полосы – все атомы отклонялись в магнитном поле двояким образом, соответствующим лишь двум возможным ориентациям магнитного момента (рис. 7.10).
) мог принимать произвольные ориентации в пространстве (т.е. в магнитном поле), то можно было ожидать непрерывного распределения попаданий атомов серебра на фотопластинку с большой плотностью попаданий в середине. Но на опыте были получены совершенно неожиданные результаты: на фотопластинке получились две резкие полосы – все атомы отклонялись в магнитном поле двояким образом, соответствующим лишь двум возможным ориентациям магнитного момента (рис. 7.10).
Этим доказывался квантовый характер магнитных моментов электронов. Количественный анализ показал, что проекция магнитного момента электрона равна магнетону Бора:
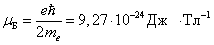 .
.
Таким образом, для атомов серебра Штерн и Герлах получили, что проекция магнитного момента атома (электрона) на направление магнитного поля численно равна магнетону Бора.
Напомним, что
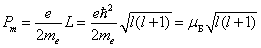 .
.
Опыты Штерна и Герлаха не только подтвердили пространственное квантование моментов импульсов в магнитном поле, но и дали экспериментальное подтверждение тому, что магнитные моменты электронов тоже состоят из некоторого числа «элементарных моментов», т.е. имеют дискретную природу. Единицей измерения магнитных моментов электронов и атомов является магнетон Бора (? – единица измерения механического момента импульса).
Кроме того, в этих опытах было обнаружено новое явление. Валентный электрон в основном состоянии атома серебра имеет орбитальное квантовое число l = 0 (s- состояние). Но при l = 0 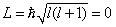 (проекция момента импульса на направление внешнего поля равна нулю). Возник вопрос, пространственное квантование какого момента импульса обнаружилось в этих опытах и проекция какого магнитного момента равна магнетону Бора.
(проекция момента импульса на направление внешнего поля равна нулю). Возник вопрос, пространственное квантование какого момента импульса обнаружилось в этих опытах и проекция какого магнитного момента равна магнетону Бора.
В 1925 г. студенты Геттингенского университета Гаудсмит и Уленбек предположили существование собственного механического момента импульса у электрона 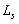 (спина) и, соответственно, собственного магнитного момента электрона Pms.
(спина) и, соответственно, собственного магнитного момента электрона Pms.
Введение понятия спина сразу объяснило ряд затруднений, имевшихся к тому времени в квантовой механике. И в первую очередь – результатов опытов Штерна и Герлаха.
Авторы дали такое толкование спина: электрон – вращающийся волчок. Но тогда следует, что «поверхность» волчка (электрона) должна вращаться с линейной скоростью, равной 300 с, где с – скорость света. От такого толкования спина пришлось отказаться.
В современном представлении – спин, как заряд и масса, есть свойство электрона.
П. Дирак впоследствии показал, что существование спина вытекает из решения релятивистского волнового уравнения Шредингера.
Из общих выводов квантовой механики следует, что спин должен быть квантован: 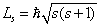 , где s – спиновое квантовое число.
, где s – спиновое квантовое число.
Аналогично, проекция спина на ось z (Lsz) (ось z совпадает с направлением внешнего магнитного поля) должна быть квантована и вектор 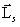 может иметь (2 s + 1) различных ориентаций в магнитном поле.
может иметь (2 s + 1) различных ориентаций в магнитном поле.
Из опытов Штерна и Герлаха следует, что таких ориентаций всего две: 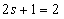 , а значит s = 1/2, т.е. спиновое квантовое число имеет только одно значение.
, а значит s = 1/2, т.е. спиновое квантовое число имеет только одно значение.
Для атомов первой группы, валентный электрон которых находится в s- состоянии (l = 0), момент импульса атома равен спину валентного электрона. Поэтому обнаруженное для таких атомов пространственное квантование момента импульса в магнитном поле является доказательством наличия у спина лишь двух ориентаций во внешнем поле. (Опыты с электронами в p- состоянии подтвердили этот вывод, хотя картина получилась более сложной) (желтая линия натрия – дуплет из-за наличия спина).
Численное значение спина электрона:
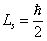 .По аналогии с пространственным квантованием орбитального момента
.По аналогии с пространственным квантованием орбитального момента 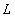 проекция спина
проекция спина 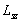 квантуется (аналогично, как
квантуется (аналогично, как 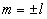 , то и
, то и 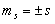 ). Проекция спина на направление внешнего магнитного поля, являясь квантовой величиной, определяется выражением:
). Проекция спина на направление внешнего магнитного поля, являясь квантовой величиной, определяется выражением:
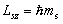 ,где
,где 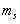 – магнитное спиновое квантовое число,
– магнитное спиновое квантовое число, 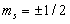 , т.е. может принимать только два значения, что и наблюдается в опыте Штерна и Герлаха.
, т.е. может принимать только два значения, что и наблюдается в опыте Штерна и Герлаха.
Итак, проекция спинового механического момента импульса на направление внешнего магнитного поля может принимать два значения:
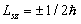 . . | (7.4.1) |
Tак как мы всегда имеем дело с проекциями, то говоря, что спин имеет две ориентации, имеем в виду две проекции.
Проекция спинового магнитного момента электрона на направление внешнего магнитного поля:
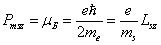 .
.
Отношение 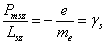 – спиновое гиромагнитное отношение
– спиновое гиромагнитное отношение
Квантовые состояния многоэлектронных атомов. Принцип Паули. Электронные оболочки и слои.
В системе одинаковых фермионовлюбые два из них не могут одновременнонаходиться в одном и том же состоянии. Отметим, что число одинаковых бозонов, находящихся в одном и том же состоянии, не лимитируется.
Напомним, что состояние электрона в атоме однозначно определяется набором четырех квантовых чисел:
- главного n 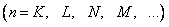 ;
;
- орбитального l 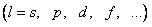 , обычно эти состояния обозначают 1 s, 2 d, 3 f;
, обычно эти состояния обозначают 1 s, 2 d, 3 f;
- магнитного 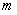
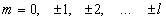
- магнитного спинового 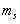 (
(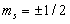 ).
).
Распределение электронов в атоме происходит по принципу Паули, который может быть сформулирован для атома в простейшем виде: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел: n, l, 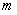 ,
, 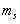 :
:
Z (n, l, 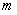 ,
, 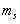 ) = 0 или 1,
) = 0 или 1,
где Z (n, l, 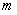 ,
, 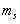 ) - число электронов, находящихся в квантовом состоянии, описываемых набором четырех квантовых чисел: n, l,
) - число электронов, находящихся в квантовом состоянии, описываемых набором четырех квантовых чисел: n, l, 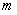 ,
, 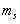 . Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме различаются значениями, по крайней мере, одного квантового числа.
. Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме различаются значениями, по крайней мере, одного квантового числа.
Максимальное число 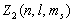 электронов, находящихся в состояниях, описываемых набором трех квантовых чисел n, l и m, и отличающихся только ориентацией спинов электронов равно:
электронов, находящихся в состояниях, описываемых набором трех квантовых чисел n, l и m, и отличающихся только ориентацией спинов электронов равно:
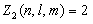 , , | (8.2.1) |
ибо спиновое квантовое число может принимать лишь два значения 1/2 и –1/2.
Максимальное число 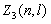 электронов, находящихся в состояниях, определяемых двумя квантовыми числами n и l:
электронов, находящихся в состояниях, определяемых двумя квантовыми числами n и l:
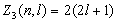 . . | (8.2.2) |
При этом вектор орбитального момента импульса электрона 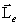 может принимать в пространстве (2 l + 1) различных ориентаций (рис. 8.1).
может принимать в пространстве (2 l + 1) различных ориентаций (рис. 8.1).
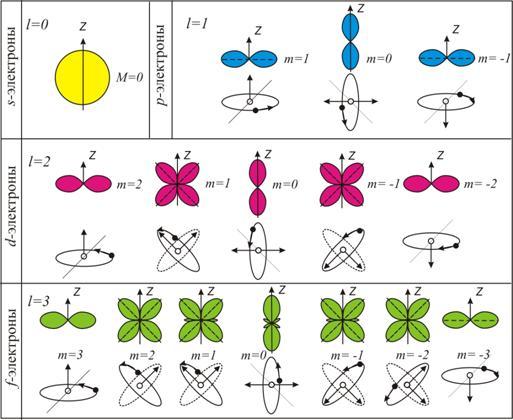
Рис. 8.1
Максимальное число электронов, находящихся в состояниях, определяемых значением главного квантового числа n, равно:
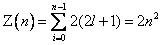 . . | (8.2.3) |
Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называется электронной оболочкой или слоем.
В каждой из оболочек электроны распределяются по подоболочкам, соответствующим данному l.
Область пространства, в которой высока вероятность обнаружить электрон, называют подоболочкой или орбиталью. Вид основных типов орбиталей показан на рис. 8.1.
Поскольку орбитальное квантовое число принимает значения от 0 до 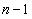 , число подоболочек равно порядковому номеру n оболочки. Количество электронов в подоболочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным l равно 2(2 l + 1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам приведено в табл. 1.
, число подоболочек равно порядковому номеру n оболочки. Количество электронов в подоболочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным l равно 2(2 l + 1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам приведено в табл. 1.
Электронная оболочка атома — область пространства вероятного местонахождения электронов, характеризующихся одинаковым значением главного квантового числа n и, как следствие, располагающихся на близких энергетических уровнях. Число электронов в каждой электронной оболочке не превышает определенного максимального значения.
Магнитные моменты атомов. Факторы Ланде. Расщепление энергетических уровней в магнитном поле. Эффект Зеемана
Магнитный момент атома слагается из орбитальных и собственных моментов входящих в его состав электронов, а также из магнитного момента ядра (который обусловлен магнитными моментами входящих в состав ядра элементарных частиц – протонов и нейтронов). Магнитный момент ядра значительно меньше моментов электронов; поэтому при рассмотрении многих вопросов им можно пренебречь и считать, что магнитный момент атома равен векторной сумме магнитных моментов электронов. Магнитный момент молекулы также можно считать равным сумме магнитных моментов входящих в её состав электронов.
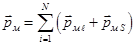
Эффект Зеемана — расщепление линий атомных спектров в магнитном поле. Эффект обусловлен тем, что в присутствии магнитного поля 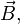 электрон, обладающий магнитным моментом
электрон, обладающий магнитным моментом 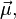 приобретает дополнительную энергию
приобретает дополнительную энергию 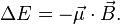 Приобретённая энергия приводит к снятию вырождения атомных состояний помагнитному квантовому числу
Приобретённая энергия приводит к снятию вырождения атомных состояний помагнитному квантовому числу 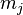 и расщеплению атомных спектральных линий.
и расщеплению атомных спектральных линий.
Множитель Ланде (гиромагнитный множитель, g-фактор) — множитель в формуле для расщепления уровней энергии в магнитном поле, определяющий масштаб расщепления в относительных единицах.
Формула, в которой он даётся:
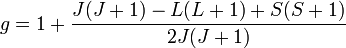
где L — значение орбитального момента атома, S — значение спинового момента атома, J — значение полного момента.
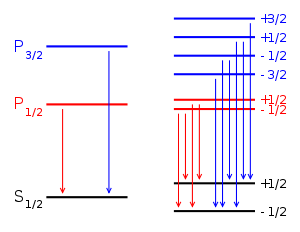
Эффект Зеемана для перехода между дублетными S и P термами (например, альфа переход в Лаймановской серии). Слева - невозмущенные уровни. Справа - уровни, расщепленные под воздействием магнитного поля. Стрелками показаны дипольно-разрешенные переходы.
 2015-02-27
2015-02-27 14041
14041
