Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение, т.е. 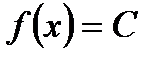 .
.
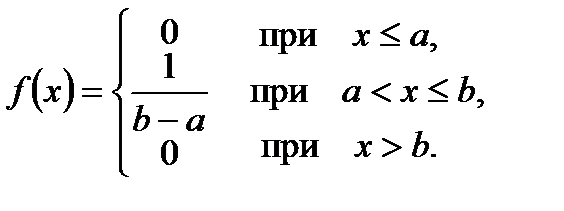
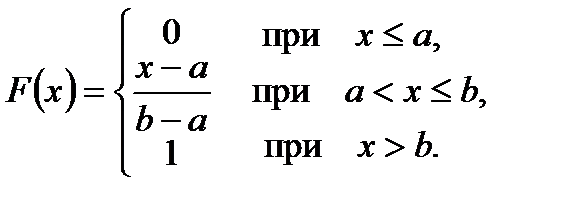
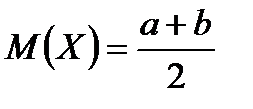 ,
, 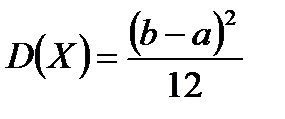
2. Показательное распределение
Показательным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью
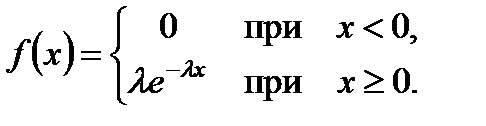
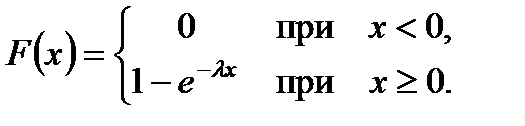
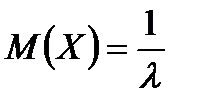 ,
, 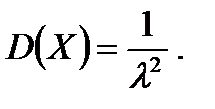
Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью
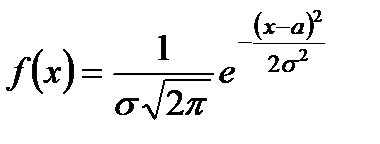 .
.
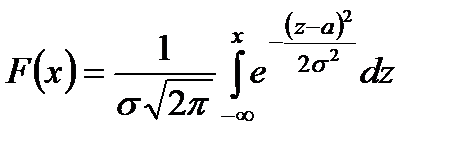
Параметры нормального распределения:
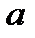 – математическое ожидание,
– математическое ожидание,  – среднее квадратическое отклонение
– среднее квадратическое отклонение
Если 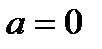 ,
, 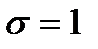 , то получаем функцию нормированного распределения:
, то получаем функцию нормированного распределения:
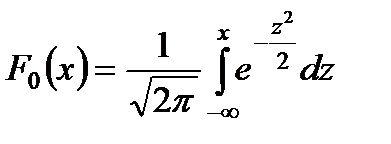 .
.
Вероятность попадания случайной величины, имеющей нормальное распределение с параметрами 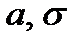 в интервалах
в интервалах 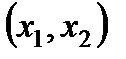 , выражается формулой:
, выражается формулой:
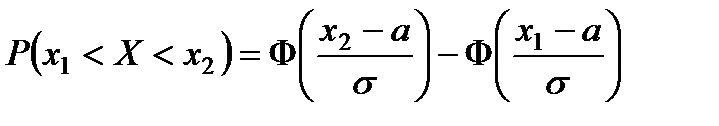 .
.
Пример 8. Автобусы идут с интервалом 5 минут. Считая, что случайная величина 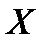 – время ожидания автобуса на остановке – распределена равномерно на указанном интервале, найти среднее время ожидания, дисперсию времени ожидания и вычислить вероятность того, что время ожидания превысит 3 минуты.
– время ожидания автобуса на остановке – распределена равномерно на указанном интервале, найти среднее время ожидания, дисперсию времени ожидания и вычислить вероятность того, что время ожидания превысит 3 минуты.
Решение. Запишем плотность функции распределения случайной величины
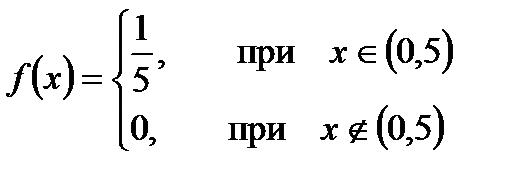 .
.
Среднее время ожидания равняется 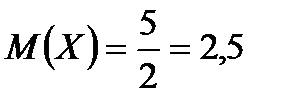 мин,
мин, 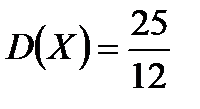 .
.
Так как 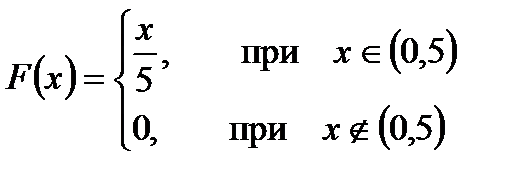 , то
, то 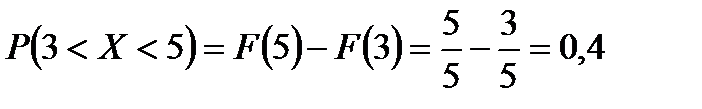 .●
.●
 2015-02-14
2015-02-14 8665
8665