Уравнение средней квадратической регрессии случайной величины Y на случайную величину Х в классе линейных функций имеет вид:
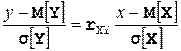 .
.
Для нахождения числовых характеристик 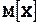 ,
, 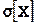 ,
, 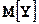 ,
, 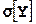 восстановим по заданному закону двумерной величины
восстановим по заданному закону двумерной величины 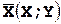 законы распределения составляющих X и Y.
законы распределения составляющих X и Y.
| X | Y | ||||||||
| P | 0,2 | 0,2 | 0,4 | 0,2 | P | 0,45 | 0,3 | 0,25 |
Математические ожидания 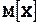 и
и 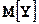 вычисляем по формулам
вычисляем по формулам
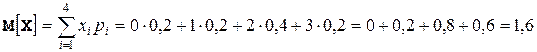 .
.
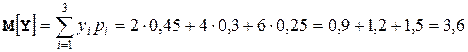 .
.
Для нахождения средних квадратических отклонений 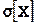 и
и 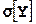 сначала вычисляем дисперсии
сначала вычисляем дисперсии 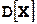 ,
, 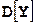 .
.
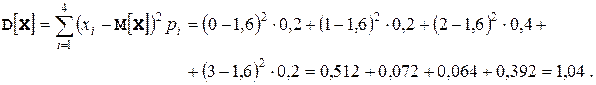
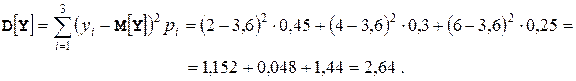
Следовательно, 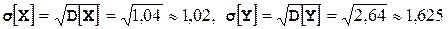 .
.
Коэффициент корреляции 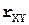 вычисляем по формуле
вычисляем по формуле 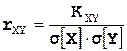 ,
,
где 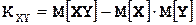 – корреляционный момент случайной величины
– корреляционный момент случайной величины 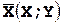 .
.
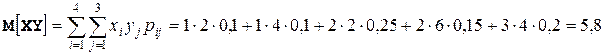 .
.
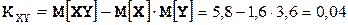 .
.  .
.
Подставляя найденные числовые характеристики в формулу, получаем уравнение прямой линии средней квадратической регрессии случайной величины Y на случайную величину Х.
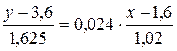 или
или 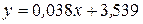 .
.
Уравнение средней квадратической регрессии случайной величины X на случайную величину Y в классе линейных функций имеет вид:
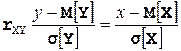 .
.
Подставляя найденные числовые характеристики, получаем следующее уравнение прямой линии регрессии X на Y
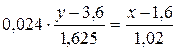 или
или 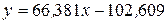 .
.
 2015-02-15
2015-02-15 2380
2380
