Первый признак сравнения. Пусть даны два ряда
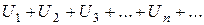 (1)
(1)
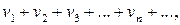 (2)
(2)
причем каждый член ряда (1) не превосходит соответствующего члена ряда (2), т.е. 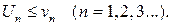 Тогда если сходится ряд (2), то сходится и ряд (1). Если расходится ряд (1), то расходится и ряд (2).
Тогда если сходится ряд (2), то сходится и ряд (1). Если расходится ряд (1), то расходится и ряд (2).
Этот признак остается в силе, если неравенства 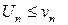 выполняются не при всех п, а лишь начиная с некоторого номера п = N.
выполняются не при всех п, а лишь начиная с некоторого номера п = N.
Второй признак сравнения. Если существует конечный и отличный от нуля предел 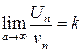 , то оба ряда
, то оба ряда 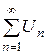 ,
, 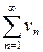 одновременно сходятся или одновременно расходятся.
одновременно сходятся или одновременно расходятся.
Радикальный признак Коши. Если для ряда
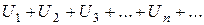
существует 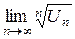 = q, то этот ряд сходится при q <1 и расходится при q >1.
= q, то этот ряд сходится при q <1 и расходится при q >1.
Признак Даламбера. Если для ряда
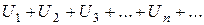
существует 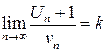 , то этот ряд сходится при k <1 и расходится при k >1.
, то этот ряд сходится при k <1 и расходится при k >1.
Интегральный признак Коши. Если f(x) при 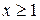 - непрерывная, положительная и монотонная убывающая функция, то ряд
- непрерывная, положительная и монотонная убывающая функция, то ряд 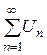 , где
, где 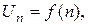 сходится или расходится в зависимости от того, сходится или расходится интеграл
сходится или расходится в зависимости от того, сходится или расходится интеграл
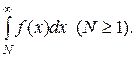
Пример. Исследовать сходимость ряда
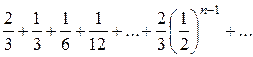
Решение: Данный ряд составлен из членов бесконечно убывающей геометрической прогрессии и поэтому сходится. Найдем его сумму 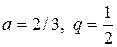 (знаменатель геометрической прогрессии). Следовательно
(знаменатель геометрической прогрессии). Следовательно
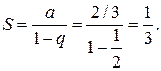
Пример. Исследовать сходимость ряда 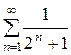 .
.
Решение: Член данного ряда меньше соответствующих членов ряда 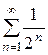 , т.е. ряда
, т.е. ряда 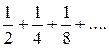
Но последний ряд сходится как бесконечно убывающая геометрическая прогрессия. Следовательно, сходится и данный ряд.
Пример. Исследовать сходимость ряда
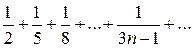
Решение: Сравним ряд с гармоническим рядом, у которого 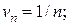
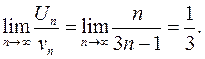
Следовательно, данный ряд расходится.
Пример. Исследовать сходимость ряда
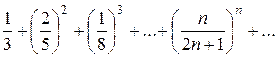
Решение: Здесь удобно применить признак Коши, поскольку 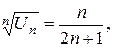 а предел
а предел
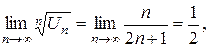
т.к. 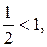 то ряд сходится.
то ряд сходится.
Пример. Исследовать сходимость ряда
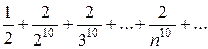 .
.
Решение: Применим признак Даламбера: имеем
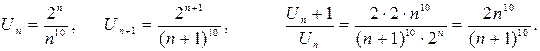
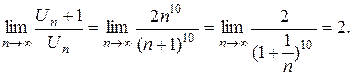
 2014-02-09
2014-02-09 3183
3183
