Показатели качества обслуживания, рассмотренные в предыдущем разделе этой лекции, интересны – при использовании технологии "коммутация каналов" – для этапов установления и прекращения соединений в ТФОП. Соответствующие операции выполняются до и после основного этапа обслуживания вызова – телефонного разговора двух абонентов (в общем случае – обмена информацией между терминалами). На этом этапе для абонентов ТФОП существенны показатели качества телефонной связи. Они определяются характеристиками транспортной сети и коммутационных станций.
Важнейшей оценкой качества телефонной связи считается мнение абонента. В качестве меры качества речи МСЭ использует среднюю экспертную оценку, известную по аббревиатуре MOS (MeanOpinionScore). Она определяется по пятибалльной шкале. В стандартах ETSI для оценки качества телефонной связи используется величина 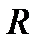 . Она связана с оценкой MOS нелинейной зависимостью. В практически значимом диапазоне MOS (от 2,5 до 4,4) применяется простое правило пересчета:
. Она связана с оценкой MOS нелинейной зависимостью. В практически значимом диапазоне MOS (от 2,5 до 4,4) применяется простое правило пересчета: 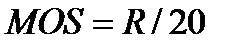 . Для основной массы абонентов приемлема оценка
. Для основной массы абонентов приемлема оценка 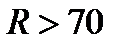 . Связь величины
. Связь величины 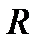 с абонентской оценкой телефонной связи иллюстрируется таблицей 1.
с абонентской оценкой телефонной связи иллюстрируется таблицей 1.
Таблица 1. Связь величины 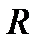 с абонентской оценкой телефонной связи
с абонентской оценкой телефонной связи
Диапазон 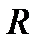 | Категория качества речи | Удовлетворенность абонентов |
| 90 – 100 | наилучшая (best) | удовлетворены в высшей степени |
| 80 – 90 | высокая (high) | удовлетворены |
| 70 – 80 | средняя (medium) | некоторые не удовлетворены |
| 60 – 70 | низкая (low) | многие не удовлетворены |
| 50 – 60 | плохая (poor) | почти все не удовлетворены |
С точки зрения восприятия звуковой информации особое значение придается показателю LSQ (Listener Speech Quality) – качеству речи для слушающего абонента. Величины LSQ, как и значения 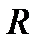 , определяются субъективно. Тем не менее, существуют и объективные оценки качества телефонной связи. Они прямо или косвенно связаны с субъективными оценками качества передачи речи. Объективные оценки, как правило, отражают один или несколько аспектов качества телефонной связи. Ценность подобных оценок заключается в том, что они позволяют планировать ТФОП с учетом требований к качеству передачи речи. Для объективных оценок обычно используются характеристики, которые могут быть измерены в процессе эксплуатации ТФОП.
, определяются субъективно. Тем не менее, существуют и объективные оценки качества телефонной связи. Они прямо или косвенно связаны с субъективными оценками качества передачи речи. Объективные оценки, как правило, отражают один или несколько аспектов качества телефонной связи. Ценность подобных оценок заключается в том, что они позволяют планировать ТФОП с учетом требований к качеству передачи речи. Для объективных оценок обычно используются характеристики, которые могут быть измерены в процессе эксплуатации ТФОП.
Оценки, подобные приведенным в таблице 1, интересны также и для других сетей связи. Правда, для обеспечения заданного уровня показателей качества обслуживания в этих сетях приходится решать ряд других задач.
На рис. 3 приведена модель тракта обмена информацией между телефонными аппаратами двух абонентов. Как и для модели, рассмотренной ранее, предполагается, что соединение установлено через 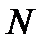 транзитных станций, а включение обоих телефонных аппаратов осуществляется по индивидуальным двухпроводным абонентским линиям. Для показателей, определяемых между абонентскими терминалами, в качестве нижнего индекса используется цифра "0". В других случаях вводятся буквенные обозначения при нормируемых показателях.
транзитных станций, а включение обоих телефонных аппаратов осуществляется по индивидуальным двухпроводным абонентским линиям. Для показателей, определяемых между абонентскими терминалами, в качестве нижнего индекса используется цифра "0". В других случаях вводятся буквенные обозначения при нормируемых показателях.
Рис. 3. Тракт обмена информацией между телефонными аппаратами двух абонентов
Одним из важнейших показателей качества телефонной связи считается величина остаточного затухания между абонентскими терминалами – 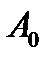 . Она определяется как разность между уровнями сигнала частотой 1020 Гц на входе и на выходе канала, который организован между абонентскими терминалами. Снижение уровня принимаемого сигнала (при значительном остаточном затухании) ухудшает восприятие речи. В сочетании с другими мешающими факторами (в частности, с шумами) рост остаточного затухания может привести к невозможности телефонного разговора.
. Она определяется как разность между уровнями сигнала частотой 1020 Гц на входе и на выходе канала, который организован между абонентскими терминалами. Снижение уровня принимаемого сигнала (при значительном остаточном затухании) ухудшает восприятие речи. В сочетании с другими мешающими факторами (в частности, с шумами) рост остаточного затухания может привести к невозможности телефонного разговора.
Требования абонентов ТФОП к остаточному затуханию разговорного тракта можно оценить при помощи сравнения с общением двух человек, находящихся на расстоянии друг от друга. Процессы, связанные с восприятием речи, очень схожи. В обоих случаях сигнал ослабевает. В таблице 2 приведены данные об изменении требований абонентов к качеству телефонной связи.
Таблица 2. Изменение требований абонентов к допустимому затуханию
| Вид соединения в ТФОП | Эквивалентное расстояние при обычном общении, м | ||||
| 1923 год | 1933 год | 1950 год | 1985 год | Оптимальное | |
| Местное | 8,3 | 3,5 | 2,0 | 0,6 | |
| Междугородное | 11,7 | 5,0 | 2,0 | 0,6 |
Очевидно, что величина остаточного затухания 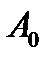 в процессе модернизации ТФОП должна уменьшаться. При цифровизации ТФОП такая возможность достигается за счет использования концепции "наложенной сети", рассмотренной в третьей лекции. Для цифрового участка ТФОП (между двумя АЦП) остаточное затухание целесообразно устанавливать на уровне 7 дБ. Эта величина относится к базовой сети, о которой говорилось во вводной лекции. Тогда в цифровой ТФОП (рис. 4) остаточное затухание разговорного тракта будет определяться параметрами абонентских линий.
в процессе модернизации ТФОП должна уменьшаться. При цифровизации ТФОП такая возможность достигается за счет использования концепции "наложенной сети", рассмотренной в третьей лекции. Для цифрового участка ТФОП (между двумя АЦП) остаточное затухание целесообразно устанавливать на уровне 7 дБ. Эта величина относится к базовой сети, о которой говорилось во вводной лекции. Тогда в цифровой ТФОП (рис. 4) остаточное затухание разговорного тракта будет определяться параметрами абонентских линий.
Рис. 4. Распределение остаточного затухания в цифровой телефонной сети
В скобках для каждого обозначения остаточного затухания (между терминалами двух абонентов – 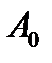 , абонентской линии –
, абонентской линии – 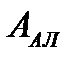 и базовой сети –
и базовой сети – 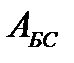 ) приведены те перспективные нормы, которые рекомендуются для цифровой ТФОП. Следует заметить, что повышение допустимой величины остаточного затухания для абонентской линии (ранее было нормировано значение 4,5 дБ) может привести к проблемам с применением технологий xDSL. Кроме того, увеличиваются затраты на построение сети доступа. Эти вопросы рассматриваются в следующей лекции.
) приведены те перспективные нормы, которые рекомендуются для цифровой ТФОП. Следует заметить, что повышение допустимой величины остаточного затухания для абонентской линии (ранее было нормировано значение 4,5 дБ) может привести к проблемам с применением технологий xDSL. Кроме того, увеличиваются затраты на построение сети доступа. Эти вопросы рассматриваются в следующей лекции.
Еще одним важным показателем качества телефонной связи в цифровой ТФОП является коэффициент искажений битов – BER (BitErrorRate). В ряде публикаций этот коэффициент называется частотой появления искаженных битов. Увеличение количества таких битов может заметно искажать речевой сигнал и существенно влиять на процессы обмена данными при использовании ресурсов ТФОП для передачи дискретной информации. Качество тракта E1, соединяющего цифровые коммутационные станции между собой, считается хорошим, если коэффициент искаженных битов не превышает уровень 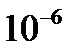 .
.
Потоки заявок
Словосочетание "поток заявок" – одно из фундаментальных понятий в теории телетрафика. Его описанию в классификации Кендалла (включая все модификации) отводится первая позиция.
Поток заявок в редких случаях можно считать детерминированным. Для него время между поступлением соседних заявок – постоянная величина. Процесс поступления заявок обычно является случайным. Длительность обслуживания заявок в большинстве случаев также будет случайной величиной. Постоянная длительность обслуживания заявок встречается в некоторых элементах инфокоммуникационных сетей чаще. Как правило, функциям 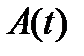 и
и 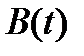 , описывающим свойства входящего потока заявок и процесса их обслуживания, свойственна ненулевая дисперсия.
, описывающим свойства входящего потока заявок и процесса их обслуживания, свойственна ненулевая дисперсия.
Этот факт иллюстрируют результаты измерений трафика, которые проводятся Операторами ТФОП. На рисунке 1 приведены статистические данные о вызовах, которые обслуживаются телефонной станцией. Статистические данные собирались о числе вызовов за каждую минуту в течение суток. Во всех случаях соединения были установлены для телефонной связи.
Рисунок 1. Количество вызовов, обслуживаемых телефонной станцией
Гистограмма, показанная на рисунке 1, была построена в результате обработки статистических данных, которые собирались в течение десяти дней. Эти десять дней соответствовали двум рабочим неделям. Конечно, такая выборка не позволяет судить об изменении количества поступающих вызовов в течение квартала или года. Правда, в некоторых случаях можно выделить тренды, описывающие изменения исследуемого процесса в течение нескольких лет. В любом случае, данные, подобные тем, что приведены на рисунке 1, представляют большой практический интерес.
Количество поступивших вызовов усреднялось по интервалам длительностью 15 минут. Такая длительность интервала очень часто используется при измерении трафика в телефонных сетях. Для сравнения на рисунке 2 показана гистограмма, которая получена при измерении трафика, поступающего в модемный пул. Все соединения в данном случае устанавливались для обмена данными или для выхода в Internet.
Рисунок 2. Количество вызовов, поступающих в модемный пул
Гистограммы, приведенные на двух рисунках, иллюстрируют существенные различия в характере потока вызовов, свойственных трафику речи и данных. Если же обратиться к потокам вызовов, поступающих в различные телефонные станции, то можно обнаружить и несоответствия для трафика одного вида. В данном случае речь идет о трафике речи. Для телефонной станции, вызовы которой иллюстрирует рисунок 1, час наибольшей нагрузки (ЧНН) приходится на дневное время. Такая ситуация характерна для телефонных станций с существенной долей абонентов делового сектора. Если телефонная станция расположена в так называемом "спальном районе", ее ЧНН приходится на вечернее время. Иногда выделяют два ЧНН – дневной и вечерний.
Следует отметить, что слово "заявка" используется как универсальный термин. Вызов – только один из примеров заявки (правда, очень важный в теории телетрафика). Поступивший вызов может породить несколько процессов (например, в системах технической эксплуатации, тарификации и других), которые не связаны с установлением соединений в инфокоммуникационной сети. Иногда в теории телетрафика используется слово "требование" как синоним термина "заявка".
В теории телетрафика – за редким исключением – рассматривают случайные потоки вызовов. Детерминированные потоки вызовов встречаются в практической деятельности очень редко. Тем не менее, именно для детерминированных потоков вызовов проще сформулировать некоторые положения теории телетрафика.
Детерминированный поток вызовов может быть представлен последовательностью 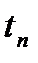 (
(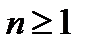 ). Вызовы поступают только в моменты времени
). Вызовы поступают только в моменты времени 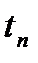 . Могут накладываться некоторые ограничения на число поступающих вызовов. Простейший случай – в любой момент времени
. Могут накладываться некоторые ограничения на число поступающих вызовов. Простейший случай – в любой момент времени 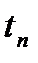 (
(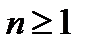 ) может поступить не более чем один вызов. Такой поток называется ординарным.
) может поступить не более чем один вызов. Такой поток называется ординарным.
На рисунке 3 показаны два способа представления потока вызовов. Способ (а) иллюстрирует изложенный выше метод описания потока вызовов. Способ (б), основанный на применении ступенчатой функции 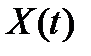 , позволяет наглядно отразить ряд свойств потока вызовов. Функция
, позволяет наглядно отразить ряд свойств потока вызовов. Функция 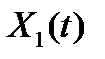 представляет ординарный поток вызовов. Очевидно, что функция
представляет ординарный поток вызовов. Очевидно, что функция 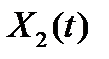 описывает неординарный поток вызовов. Обе функции для наглядности имеют приращения в одних и тех же точках по оси абсцисс. Для функции
описывает неординарный поток вызовов. Обе функции для наглядности имеют приращения в одних и тех же точках по оси абсцисс. Для функции 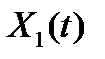 все приращения по оси одинаковы, так как в любой момент времени
все приращения по оси одинаковы, так как в любой момент времени 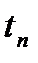 поступает один вызов. Для неординарного потока на рисунке 3 показана возможность поступления двух (
поступает один вызов. Для неординарного потока на рисунке 3 показана возможность поступления двух (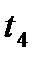 и
и 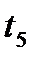 ) и даже трех (
) и даже трех (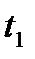 ) вызовов, что определяется величиной приращения функции
) вызовов, что определяется величиной приращения функции 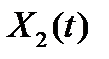 по оси ординат.
по оси ординат.
Рисунок 3. Два способа представления потока вызовов
Ось абсцисс для некоторых приложений удобно определять как последовательность промежутков (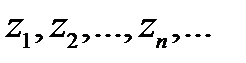 ) между вызовами. Величина
) между вызовами. Величина 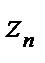 представляет собой разность
представляет собой разность 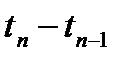 для
для 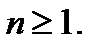
Различия между детерминированным и случайным потоками вызовов можно свести к свойствам функции 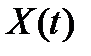 . Для случайного потока вызовов и моменты
. Для случайного потока вызовов и моменты 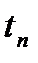 , и приращения функции
, и приращения функции 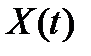 уже нельзя рассматривать как детерминированные. В телефонной связи обычно рассматриваются финитные случайные потоки, для которых математическое ожидание числа вызовов, поступивших за известный период времени, представляет собой конечную величину. Более того, обычно предполагают, что потоки вызовов обладают свойством рекуррентности. Поток вызовов считается рекуррентным, если промежутки времени между вызовами (
уже нельзя рассматривать как детерминированные. В телефонной связи обычно рассматриваются финитные случайные потоки, для которых математическое ожидание числа вызовов, поступивших за известный период времени, представляет собой конечную величину. Более того, обычно предполагают, что потоки вызовов обладают свойством рекуррентности. Поток вызовов считается рекуррентным, если промежутки времени между вызовами (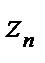 ) независимы и одинаково распределены. Для полноценного описания рекуррентного потока необходимо знать функцию распределения (ФР) длительности интервалов между вызовами –
) независимы и одинаково распределены. Для полноценного описания рекуррентного потока необходимо знать функцию распределения (ФР) длительности интервалов между вызовами – 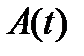 :
:
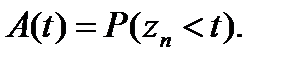 (1)
(1)
Если случайные величины 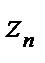 нельзя считать независимыми, то ФР
нельзя считать независимыми, то ФР 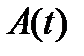 следует заменить более сложной функцией. Фактически необходимо задать ФР, определяющую взаимосвязь между величинами
следует заменить более сложной функцией. Фактически необходимо задать ФР, определяющую взаимосвязь между величинами 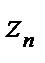 . Подобные потоки в классической теории телетрафика обычно не рассматриваются.
. Подобные потоки в классической теории телетрафика обычно не рассматриваются.
Важное свойство некоторых классов потоков вызовов – отсутствие последействия. Допустим, что мы рассматриваем поток вызовов после какого-то момента времени 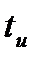 . Если его характеристики не зависят от поведения потока для
. Если его характеристики не зависят от поведения потока для 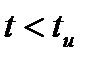 , то можно говорить об отсутствии последействия. Для потока вызовов без последействия характерно следующее: для двух попарно не пересекающихся промежутков времени разности функций
, то можно говорить об отсутствии последействия. Для потока вызовов без последействия характерно следующее: для двух попарно не пересекающихся промежутков времени разности функций 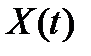 будут независимыми случайными величинами.
будут независимыми случайными величинами.
Важным атрибутом потока вызовов следует считать стационарность. Рассмотрим конечную совокупность непересекающихся интервалов времени. Если вероятность поступления 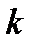 вызовов –
вызовов – 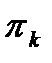 не меняется при сдвиге этой совокупности интервалов на любой отрезок времени, то поток стационарен. Допустим, что интересна вероятность
не меняется при сдвиге этой совокупности интервалов на любой отрезок времени, то поток стационарен. Допустим, что интересна вероятность 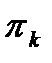 для отрезка
для отрезка 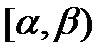 –
– 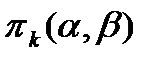 . Для стационарного потока искомая вероятность зависит не от величин
. Для стационарного потока искомая вероятность зависит не от величин 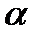 и
и 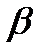 , а только от их разности.
, а только от их разности.
Для потока вызовов иногда определяют вероятность поступления хотя бы 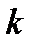 вызовов –
вызовов – 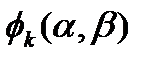 . Эта вероятность позволяет сформулировать условие ординарности потока вызовов. Он считается ординарным, если при
. Эта вероятность позволяет сформулировать условие ординарности потока вызовов. Он считается ординарным, если при 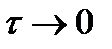 отношение
отношение
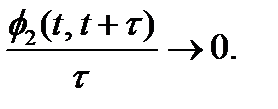 (2)
(2)
равномерно на любом конечном интервале времени. Параметром потока 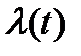 называется следующий предел (если, конечно, он существует):
называется следующий предел (если, конечно, он существует):
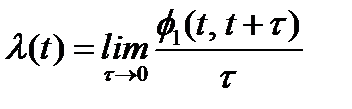 . (3)
. (3)
В телефонии, как и в ряде других приложений, часто используют предположение о том, что входящий поток вызовов является простейшим. Такому потоку присущи три важных свойства: он стационарен, ординарен и не имеет последействия. Это означает, что 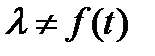 . Распределение длин промежутков между вызовами для простейшего потока подчиняется экспоненциальному закону:
. Распределение длин промежутков между вызовами для простейшего потока подчиняется экспоненциальному закону:
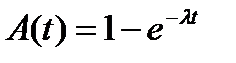 . (4)
. (4)
Вероятность поступления ровно 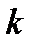 вызовов за период длительностью
вызовов за период длительностью 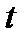 определяется распределением Пуассона:
определяется распределением Пуассона:
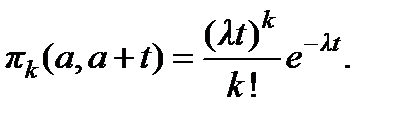 (5)
(5)
Среднее число заявок, поступающих за время 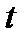 , составляет
, составляет 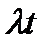 . Математическое ожидание числа заявок, поступающих за единицу времени, называется интенсивностью потока –
. Математическое ожидание числа заявок, поступающих за единицу времени, называется интенсивностью потока – 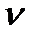 . Для простейшего потока
. Для простейшего потока 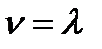 . Поэтому величину
. Поэтому величину 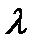 (вместо
(вместо 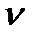 ) обычно называют интенсивностью потока заявок. Правильным названием величины
) обычно называют интенсивностью потока заявок. Правильным названием величины 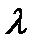 следует считать "параметр потока".
следует считать "параметр потока".
Замечательным свойством обладает объединение независимых простейших потоков вызовов с интенсивностями 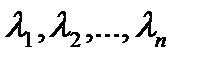 и так далее. Результатом операции объединения является также простейший поток с интенсивностью
и так далее. Результатом операции объединения является также простейший поток с интенсивностью 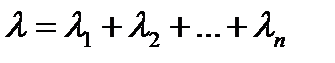 .
.
Во многих случаях сумма большого числа малых стационарных потоков близка к простейшему потоку. Это положение часто используется в теории телетрафика. Оно помогают существенно упростить анализ СМО. Правда, в ряде практических задач речь идет о суммировании сравнительно малого числа потоков.
Для телефонной сети, построенной на базе технологии "коммутация каналов", наиболее достоверным выглядит предположение об ординарности потока вызовов. Действительно, телефонные вызовы не приходят пачками в отличие от заявок в некоторых других инфокоммуникационных системах. Свойство стационарности опровергает первый рисунок. Правда, расчет телефонной сети осуществляется для ЧНН, что необходимо для соблюдения заданных показателей качества обслуживания вызовов в любое время суток. В пределах ЧНН допущение о стационарном характере потока вызовов в телефонной сети считается допустимым. Гипотеза об отсутствии последействия опровергается ситуациями, когда один вызов порождает несколько других. Например, в процессе телефонного разговора с одноклассником Вы решили собрать школьных друзей на дачу. Ваш друг берет на себя задачу обзвонить их. В результате осуществляется ряд вызовов (возможно, что процесс будет чем-то похож на "цепную реакцию"). С другой стороны, при большой емкости телефонной станции предположение об отсутствии последействия может быть обосновано математически.
Использование гипотезы о пуассоновском характере потока вызовов не всегда правомерно. К сожалению, большинство других рекуррентных потоков, интересных с точки зрения адекватного представления исследуемого процесса, не позволяют получить формулы для расчета всех необходимых характеристик СМО.
Для некоторых приложений целесообразно использовать ступенчатые функции при анализе сложных СМО. В классификации Кендалла СМО такого рода можно представить следующим образом:
 (6)
(6)
Символ "  " образован из двух букв. Буква
" образован из двух букв. Буква 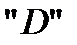 используется для обозначения детерминированного распределения. Предшествующая ей буква
используется для обозначения детерминированного распределения. Предшествующая ей буква 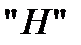 – по аналогии с гиперэкспоненциальным распределением – указывает на то, что рассматривается "смесь" функций. Ранее использовался также символ
– по аналогии с гиперэкспоненциальным распределением – указывает на то, что рассматривается "смесь" функций. Ранее использовался также символ 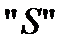 – первая буква в слове "ступенька" на английском языке.
– первая буква в слове "ступенька" на английском языке.
Для потока заявок, поступающего в СМО вида (6), распределение интервалов между вызовами удобно определять преобразованием Лапласа-Стилтьеса – 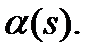 На основе первой теоремы смещения (она была рассмотрена в первой лекции) эта функция может быть представлена в таком виде:
На основе первой теоремы смещения (она была рассмотрена в первой лекции) эта функция может быть представлена в таком виде:
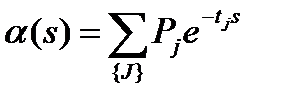 . (7)
. (7)
Если обозначить через 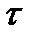 наибольший общий делитель для всех значений
наибольший общий делитель для всех значений 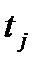 из множества
из множества 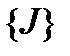 , то формулу (7) можно переписать в иной редакции:
, то формулу (7) можно переписать в иной редакции:
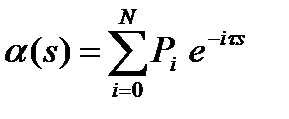 . (8)
. (8)
Точка 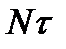 определяет такое значение
определяет такое значение 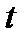 , после которого все величины приращений
, после которого все величины приращений 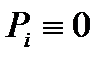 . Можно показать, что даже при
. Можно показать, что даже при 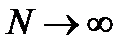 усложнения процесса вычисления ФР не происходит.
усложнения процесса вычисления ФР не происходит.
На рисунке 4 представлена модель СМО, для которой можно выделить разные виды входящих и выходящих потоков. Рассматривается гипотетическая модель, но можно представить какой-либо элемент инфокоммуникационной системы с такой (или близкой) совокупностью входящих и выходящих потоков.
Рисунок 4. СМО с различными видами входящих и выходящих потоков
Анализируемая СМО расположена в правой части предложенной модели. Для нее следует выделить три вида входящих потоков. Во-первых, 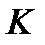 потоков выходит из такого же числа СМО. Они, одновременно, являются входящими потоками для рассматриваемой СМО. Во-вторых,
потоков выходит из такого же числа СМО. Они, одновременно, являются входящими потоками для рассматриваемой СМО. Во-вторых, 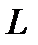 потоков создают терминалы, посредством которых пользователи осуществляют обмен информацией. В-третьих, в некоторых СМО существует своего рода петля обратной связи, которая образует путь для еще одного вида потока заявок.
потоков создают терминалы, посредством которых пользователи осуществляют обмен информацией. В-третьих, в некоторых СМО существует своего рода петля обратной связи, которая образует путь для еще одного вида потока заявок.
В некоторых случаях выделяют пуассоновский поток первого и второго рода. Пуассоновский поток первого рода создается бесконечным числом источников трафика. Понятно, что это некая идеализация. Пуассоновский поток второго рода генерируется конечным числом источников трафика.
Некоторые заявки могут теряться по различным причинам (ограниченное число мест для ожидания, чрезмерная задержка обслуживания и так далее). Поэтому в нижней части нашей модели показан поток потерянных заявок. На выходе СМО формируется 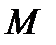 выходящих потоков.
выходящих потоков.
На рисунке 5 показана модель сети доступа, позволяющая выделить, как минимум, два вида потоков входящего вызова. Эти потоки порождают заявки, попадающие на вход СМО, которая формализует некое гипотетическое устройство обработки вызовов.
Рисунок 5. Модель сети доступа с двумя видами потоков вызовов
Предполагается, что коммутационное поле цифровой АТС поддерживает два типа интерфейсов. Выносные модули включаются по интерфейсу V5.2, которому свойственна высокая концентрация потока вызовов. Индивидуальные двухпроводные физические цепи включаются по интерфейсу Z. Обычно эти линии создают небольшой трафик. В правой части рисунка 5 показана исследуемая СМО, на вход которой поступают два вида потоков вызовов, численность которых равна 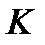 и
и 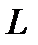 соответственно.
соответственно.
Самая лучшая – для исследования СМО – ситуация подразумевает, что оба типа потоков являются пуассоновскими. Тогда суммарный 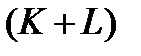 поток можно считать также пуассоновским. В противном случае определение характера потока, поступающего на вход СМО, существенно усложняется. Правда, для тех рекуррентных потоков, которые могут быть представлены распределением (8), задача упрощается. Для объединенного потока преобразование Лапласа-Стилтьеса ФР интервалов между вызовами –
поток можно считать также пуассоновским. В противном случае определение характера потока, поступающего на вход СМО, существенно усложняется. Правда, для тех рекуррентных потоков, которые могут быть представлены распределением (8), задача упрощается. Для объединенного потока преобразование Лапласа-Стилтьеса ФР интервалов между вызовами – 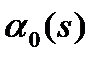 также определяет ступенчатую функцию:
также определяет ступенчатую функцию:
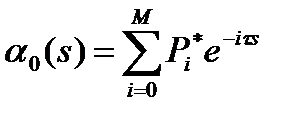 . (9)
. (9)
Конечно, определение верхнего предела суммирования – 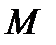 и (главное) величин приращений –
и (главное) величин приращений – 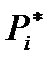 представляет собой нетривиальную процедуру. Переход к моделям, для которых преобразование Лапласа-Стилтьеса ФР интервалов между вызовами представимо формулой (8), целесообразен в тех случаях, когда гипотеза о простейшем потоке далека от реальности.
представляет собой нетривиальную процедуру. Переход к моделям, для которых преобразование Лапласа-Стилтьеса ФР интервалов между вызовами представимо формулой (8), целесообразен в тех случаях, когда гипотеза о простейшем потоке далека от реальности.
Некоторые дополнения и обобщения:
Математическое ожидание числа вызовов, поступающих в интервале времени 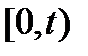 , называется ведущей функции потока –
, называется ведущей функции потока – 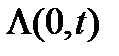 . Потоки с непрерывной ведущей функций называются регулярными, а со ступенчатой – сингулярные. Ранее теория телетрафика изучала только регулярные потоки.
. Потоки с непрерывной ведущей функций называются регулярными, а со ступенчатой – сингулярные. Ранее теория телетрафика изучала только регулярные потоки.
Важными свойствами потоков считаются стационарность, ординарность, отсутствие последействия.
Параметром потока 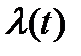 называется предел отношения вероятности поступления хотя бы одного вызова за время
называется предел отношения вероятности поступления хотя бы одного вызова за время 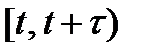 к длине этого интервала времени
к длине этого интервала времени 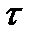 при
при 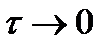 :
:
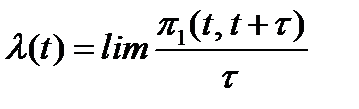
Простейший поток
Вероятность поступления ровно 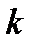 вызовов за период длительностью
вызовов за период длительностью 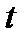 определяется распределением Пуассона:
определяется распределением Пуассона:
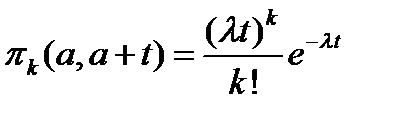 .
.
Этому потоку присущи три важных свойства: он стационарен, ординарен и не имеет последействия. Это означает, что 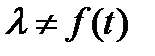 . Распределение интервалов между моментами поступления вызовов определяется таким законом:
. Распределение интервалов между моментами поступления вызовов определяется таким законом:
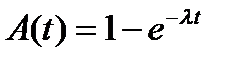 .
.
Потоки заявок (продолжение)
Основной акцент в предыдущей лекции был сделан на характеристиках простейшего потока заявок. Этому потоку свойственны: стационарность, ординарность и отсутствие последействия.
Вероятность поступления ровно 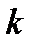 вызовов за период длительностью
вызовов за период длительностью 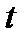 определяется распределением Пуассона:
определяется распределением Пуассона:
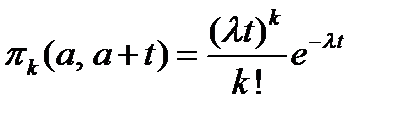 . (1)
. (1)
Распределение интервалов между моментами поступления вызовов определяется экспоненциальным законом:
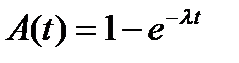 . (2)
. (2)
Практический интерес для расчета сетей и систем связи (следовательно, и для теории телетрафика) представляют потоки заявок, отличающиеся от простейшего потока. Ряд таких потоков заявок рассматривается в этой лекции.
1. Нестационарный и неординарный пуассоновские потоки
Нестационарный пуассоновский поток – это ординарный поток без последействия, для которого в любой момент времени 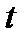 существует конечный параметр
существует конечный параметр 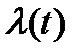 . Этот параметр зависит от момента времени
. Этот параметр зависит от момента времени 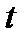 .
.
Рассматриваемый поток называют также потоком с переменным параметром или нестационарным простейшим потоком. Вероятность поступления точно 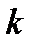 вызовов за промежуток времени
вызовов за промежуток времени 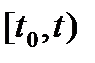 определяется следующим образом:
определяется следующим образом:
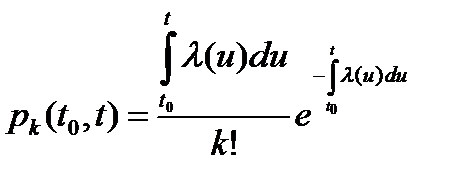 . (3)
. (3)
Если поток стационарен, то 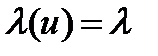 . Тогда формула (3) легко преобразуется в формулу (1). Напомним, что параметром потока
. Тогда формула (3) легко преобразуется в формулу (1). Напомним, что параметром потока 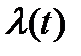 называется предел отношения вероятности поступления хотя бы одного вызова за время
называется предел отношения вероятности поступления хотя бы одного вызова за время 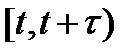 к длине этого интервала времени
к длине этого интервала времени 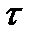 при
при 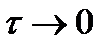 :
:
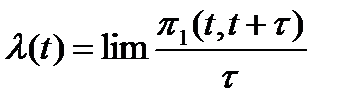 (4)
(4)
Неординарный пуассоновский поток – это стационарный поток без последействия, для которого одновременно могут поступать 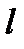 заявок. Обычно предполагается, что
заявок. Обычно предполагается, что 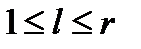 . Величину
. Величину 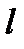 называют характеристикой неординарности потока заявок. Можно выделить два типичных случая:
называют характеристикой неординарности потока заявок. Можно выделить два типичных случая:
· значение 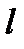 – постоянная величина (тогда формула (1) позволяет рассчитать вероятность появления "пачки" вызовов размером
– постоянная величина (тогда формула (1) позволяет рассчитать вероятность появления "пачки" вызовов размером 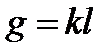 );
);
· значение 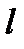 – переменная величина (тогда определяется вероятность
– переменная величина (тогда определяется вероятность 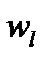 , оценивающая возможность появления "пачки", состоящей из
, оценивающая возможность появления "пачки", состоящей из 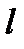 заявок).
заявок).
Общий параметр потока во втором случае оценивается следующим образом:
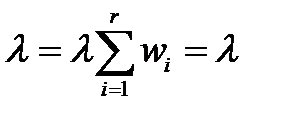 . (5)
. (5)
Интенсивность (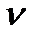 ) неординарного пуассоновского потока больше его параметра (
) неординарного пуассоновского потока больше его параметра (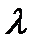 ):
):
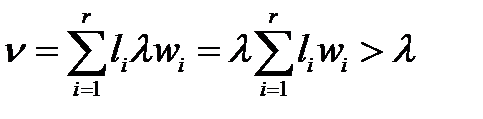 . (6)
. (6)
Интерес к нестационарным пуассоновским потокам объясняется природой трафика в телефонной сети. Неординарные потоки заявок циркулируют во многих современных системах связи. Первый пример такого потока может быть найден в системе телеграфной связи, когда диспетчер разносил по рабочим местам стопки сообщений для их подготовки и последующей отправки.
2. Потоки с простым последействием
Для потока с простым последействием важнейшей характеристикой считается зависимость параметра потока от состояния СМО в любой момент времени 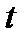 .
.
Если рассматривать коммутационное поле телефонной станции, то можно выделить множество 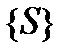 , описывающее все возможные состояния. Каждый элемент множества отражает, например, состояние элемента коммутации. Если этот элемент пребывает в двух состояниях (включено – выключено), то для
, описывающее все возможные состояния. Каждый элемент множества отражает, например, состояние элемента коммутации. Если этот элемент пребывает в двух состояниях (включено – выключено), то для 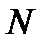 элементов множество состояний будет определяться величиной
элементов множество состояний будет определяться величиной 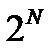 .
.
Для анализа обычно выделяют микро- и макросостояния коммутационного поля. Выбор между ними осуществляется с учетом природы решаемой задачи. Он также будет зависеть от свойств коммутационного поля. Для исследования коммутационных полей под макросостоянием обычно понимают только число занятых входов или выходов. Параметром потока в состоянии 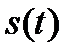 считается следующий предел:
считается следующий предел:
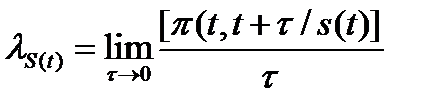 . (7)
. (7)
В числителе указана вероятность поступления на отрезке 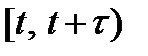 одного и более вызовов, если в момент времени
одного и более вызовов, если в момент времени 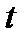 СМО находилась в состоянии
СМО находилась в состоянии 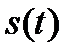 . Эта формула позволяет сформулировать такое определение: поток с простым последействием является ординарным, для которого в любой момент времени
. Эта формула позволяет сформулировать такое определение: поток с простым последействием является ординарным, для которого в любой момент времени 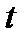 существует конечный параметр в состоянии
существует конечный параметр в состоянии 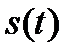 , зависящий только от состояния СМО –
, зависящий только от состояния СМО – 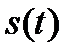 и независящий от процесса обслуживания заявок до момента времени
и независящий от процесса обслуживания заявок до момента времени 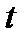 .
.
Рассматриваемое последействие называется простым по следующей причине: для расчета параметра потока достаточно знать состояние СМО 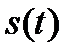 . Это означает, что поток с простым последействием не относится к классу стационарных потоков. Его параметр зависит от времени. Эта зависимость проявляется через состояние
. Это означает, что поток с простым последействием не относится к классу стационарных потоков. Его параметр зависит от времени. Эта зависимость проявляется через состояние 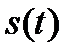 .
.
3. Симметричный и примитивный потоки
Эти два вида потоков можно рассматривать как частные случаи потока с простым последействием. Симметричным потоком называется поток с простым последействием, параметр которого 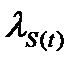 в любой произвольный момент времени
в любой произвольный момент времени 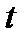 зависит лишь от числа обслуживаемых в этот момент времени вызовов
зависит лишь от числа обслуживаемых в этот момент времени вызовов 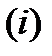 . Этот означает, что параметр потока не зависит от других свойств состояния
. Этот означает, что параметр потока не зависит от других свойств состояния 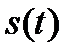 . Тогда обозначение
. Тогда обозначение 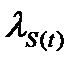 можно заменить на
можно заменить на 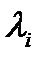 .
.
Примитивным потоком называется такой симметричный поток, параметр которого 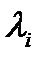 прямо пропорционален числу свободных в данный момент времени источников трафика:
прямо пропорционален числу свободных в данный момент времени источников трафика:
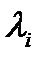
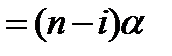 . (8)
. (8)
В этой формуле 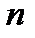 – общее число источников трафика,
– общее число источников трафика, 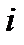 – число занятых источников трафика,
– число занятых источников трафика, 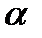 – параметр потока источника в свободном состоянии. Этот параметр считается постоянной величиной, а параметр примитивного потока
– параметр потока источника в свободном состоянии. Этот параметр считается постоянной величиной, а параметр примитивного потока 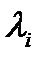 убывает по мере роста численности занятых источников трафика.
убывает по мере роста численности занятых источников трафика.
Математическое ожидание (среднее значение) параметра примитивного потока 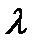 определяется с учетом вероятности нахождения СМО в состоянии
определяется с учетом вероятности нахождения СМО в состоянии 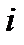 –
– 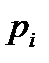 (занятости
(занятости 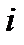 источников трафика):
источников трафика):
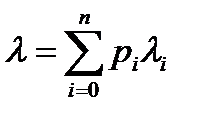 . (9)
. (9)
Функция распределения вида 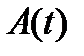 для каждого источника трафика определяется таким соотношением:
для каждого источника трафика определяется таким соотношением:
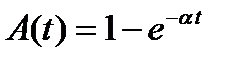 . (10)
. (10)
Для достаточно больших значений 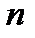 и малых величин
и малых величин 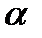 примитивный поток очень похож на простейший с интенсивностью заявок
примитивный поток очень похож на простейший с интенсивностью заявок 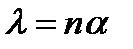 .
.
4. Поток с повторными вызовами
Поток заявок (вызовов), поступающих в СМО (местную телефонную станцию), часто можно рассматривать как совокупность первичных и повторных заявок. Первичная заявка генерируется терминалом, ранее не занятым исходящим соединением. Повторная заявка создается терминалом, который (в недавнем прошлом) получил отказ в обслуживании. Параметр потока первичных вызовов (заявок) можно считать независящим от состояния местной телефонной станции. Для параметра повторных вызовов такое допущение нельзя считать приемлемым. Чем больше занято обслуживающих приборов, тем больше параметр потока повторных вызовов.
Различить первичные и повторные заявки достаточно сложно. В любом случае, надо учитывать, что поток, интенсивность которого измеряется на входе СМО, образован двумя видами заявок – первичными и повторными. Способы снижения интенсивности повторных заявок – предмет отдельного анализа.
7. Выходящие потоки
Свойства выходящих потоков часто представляют большой практический интерес. Эти потоки являются входящими для последующих СМО. Свойства выходящего потока зависят от множества факторов, среди которых следует выделить:
· характеристики входящего потока заявок;
· длительность обслуживания заявок и соответствующий закон распределения;
· численность обслуживающих приборов;
· алгоритм выбора заявки на обслуживание.
Наиболее просто исследовать однолинейную СМО с ожиданием, на вход которой поступает пуассоновский входящий поток. Для такой модели известно преобразование Лапласа-Стилтьеса функции распределения интервалов между заявками, покидающими СМО:
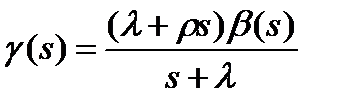 . (16)
. (16)
Из этого выражения можно найти коэффициент вариации длительности интервалов между заявками, покидающими СМО – 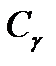 . Для этого необходимо взять первую и вторую производные от
. Для этого необходимо взять первую и вторую производные от 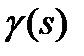 . В точке
. В точке 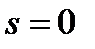 эти производные определяют первый и второй моменты функции распределения интервалов между заявками, покидающими СМО. Из-за отсутствия потерь заявок первый момент составляет
эти производные определяют первый и второй моменты функции распределения интервалов между заявками, покидающими СМО. Из-за отсутствия потерь заявок первый момент составляет 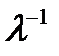 . По двум моментам легко определяется величина
. По двум моментам легко определяется величина 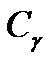 :
:
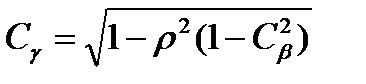 . (17)
. (17)
В этой формуле величина 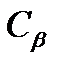 определяет коэффициент вариации длительности обслуживания заявок. Очевидно, что выходящий поток будет близок к простейшему (по критерию
определяет коэффициент вариации длительности обслуживания заявок. Очевидно, что выходящий поток будет близок к простейшему (по критерию 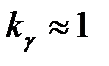 ) при соблюдении хотя бы одного из двух условий:
) при соблюдении хотя бы одного из двух условий:
· низкая загрузка системы 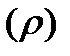 , что приближает величину
, что приближает величину 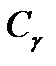 к единице вне зависимости от характера функции
к единице вне зависимости от характера функции 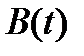 ;
;
· близость коэффициента 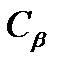 к единице (в этом случае не так существенна величина загрузки системы).
к единице (в этом случае не так существенна величина загрузки системы).
Строго говоря, условие 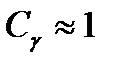 нельзя считать достаточным для утверждения о пуассоновском характере выходящего потока. Можно подобрать ряд распределений, для которых
нельзя считать достаточным для утверждения о пуассоновском характере выходящего потока. Можно подобрать ряд распределений, для которых 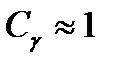 , но функция распределения длительности интервалов между вызовами не будет похожа на экспоненциальный закон.
, но функция распределения длительности интервалов между вызовами не будет похожа на экспоненциальный закон.
Обслуживание заявок
В большинстве СМО время обслуживания заявок представляет собой случайную величину. Следовательно, полная информация о длительности обслуживания заявок может быть представлена ФР – 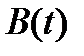 . Будем считать, что функция имеет преобразование Лапласа-Стилтьеса –
. Будем считать, что функция имеет преобразование Лапласа-Стилтьеса – 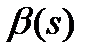 .
.
По аналогии с лекцией о потоках заявок рассмотрим статистические данные о времени телефонного разговора и длительности занятия модемного пула – рисунки 1 и 2.
Рисунок 1. Изменение среднего времени телефонного разговора в сутки
Статистические данные, использованные для построения той гистограммы, которая приведена на рисунке 1, были собраны в 1973 году. Поэтому измеряемая величина связана только с трафиком речи. Передача факсимильных сообщений в это время была большой редкостью, а трафик данных вообще отсутствовал. Следует отметить, что длительность местных соединений при сборе статистических данных не учитывалась. Это означает, что рассматривался междугородный и международный трафик речи. Необходимо также подчеркнуть, что измеряемая величина характерна для соединений, устанавливаемых со стационарных телефонных терминалов (в 1973 году мобильной связи еще не было). Для сетей мобильной связи характерны иные распределения и численности вызовов, и средней длительности разговоров.
Рисунок 2. Изменение среднего времени занятия модемного пула
Очевидно, два графика не идентичны ни с точки зрения закона распределения, ни по численным значениям математического ожидания длительности обслуживания заявок. Напомним, что оба графика представляют динамику изменения средних величин. Среди тех распределений 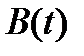 , которые представляют практический интерес, можно выделить семь законов.
, которые представляют практический интерес, можно выделить семь законов.
Во многих исследованиях, касающихся телефонного трафика, используется предположение об экспоненциальном распределении:
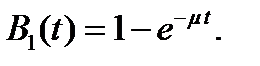 (1)
(1)
Экспоненциальное распределение существенно упрощает исследование СМО. Кроме того, многие распределения, более реальные с практической точки зрения, имеют коэффициент вариации менее единицы. Это означает, что результаты, полученные для экспоненциального распределения, позволяют оценить характеристики исследуемой СМО "сверху" – для пессимистического сценария. Тем не менее, для многих ситуаций гипотезу об экспоненциальном распределении длительности обслуживания заявок следует считать очень грубым приближением. Это утверждение справедливо и для многих других законов распределения с модой в точке 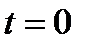 .
.
Распределения с коэффициентом вариации менее единицы часто представимы с помощью распределения Эрланга 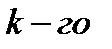 порядка. Характеристики этого распределения были приведены в предыдущей лекции. Напомним выражение для ФР:
порядка. Характеристики этого распределения были приведены в предыдущей лекции. Напомним выражение для ФР:
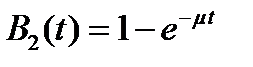
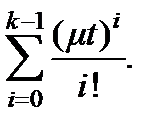 (2)
(2)
При 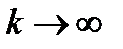 распределение Эрланга вырождается. Этот случай рассматривается как самостоятельное распределение – постоянная длительность обслуживания, равная
распределение Эрланга вырождается. Этот случай рассматривается как самостоятельное распределение – постоянная длительность обслуживания, равная 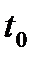 . Для ряда технических систем СМО с постоянным временем обслуживания хорошо описывает процессы функционирования. Функцию
. Для ряда технических систем СМО с постоянным временем обслуживания хорошо описывает процессы функционирования. Функцию 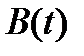 проще записать через преобразование Лапласа-Стилтьеса:
проще записать через преобразование Лапласа-Стилтьеса:
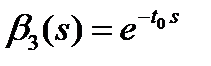 . (3)
. (3)
Распределения с коэффициентом вариации более единицы можно представить с помощью гиперэкспоненциального распределения. На практике чаще всего используют простейшую форму гиперэкспоненциального распределения:
· длительность обслуживания заявок подчиняется экспоненциальному закону с интенсивностью 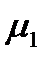 с вероятностью
с вероятностью 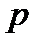 ;
;
· длительность обслуживания заявок подчиняется экспоненциальному закону с интенсивностью 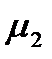 с вероятностью
с вероятностью 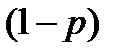 ;
;
Эти предположения позволяют представить ФР длительности обслуживания в таком виде:
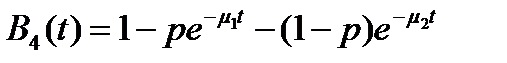 . (4)
. (4)
Комбинация эрланговского и гиперэкспоненциального распределения позволяет хорошо аппроксимировать множество непрерывных функций. Соответствующая ФР может быть определена так:
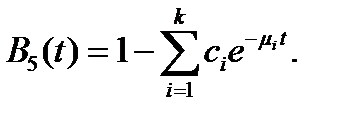 (5)
(5)
Для коэффициентов 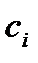 должны выполняться два условия:
должны выполняться два условия:
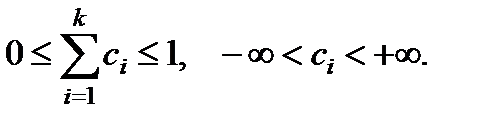 (6)
(6)
Следующее распределение – равномерное на отрезке времени 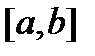 . Оно также было рассмотрено на первой лекции. Выражение для ФР записывается в следующем виде:
. Оно также было рассмотрено на первой лекции. Выражение для ФР записывается в следующем виде:
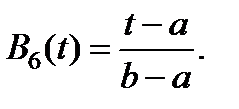 (7)
(7)
Последнее распределение относится к дискретным. Речь идет о ступенчатой функции, для которой справедливо такой преобразование Лапласа-Стилтьеса:
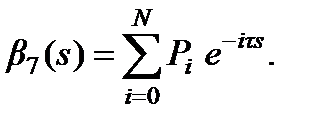 (8)
(8)
Конечно, можно привести ряд других примеров, но далее иные ФР рассматриваться не будут.
 2015-03-27
2015-03-27 2269
2269
