2.3.1. Определение. Произведением строки A =(а 1, а 2, … аn) на столбец B =(b 1, b 2, … bn)T называется число a 1 b 1+ a 2 b 2+…+ anbn.
Это произведение обозначается через AB.
Например, если A =(1, 2, 4), B =(-1, 2, 3)Т, то
AB =(1, 2, 4) 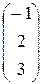 =1×(-1)+2×2+4×3=15.
=1×(-1)+2×2+4×3=15.
Таким образом, по определению
(а 1, а 2, … аn) 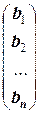 = a 1 b 1+ a 2 b 2+…+ anbn,
= a 1 b 1+ a 2 b 2+…+ anbn,
то есть для того, чтобы строку умножить на столбец, необходимо, чтобы число элементов строки равнялось числу элементов столбца.
2.3.2. Определение. Произведением матрицы A =(aij) m ´ n на матрицу B =(bij) n ´ k называется матрица C =(cij) m ´ k, такая, что
cij = ai 1 b 1 j + ai 2 b 2 j +…+ ainbnj.
Произведение матрицы A на матрицу B обозначается через AB.
Таким образом, AB =(ai 1 b 1 j + ai 2 b 2 j +…+ ainbnj) m ´ n, то есть элемент cij произведения A на B получается как произведение i - й строки (то есть строки под номером i) матрицы A на j - й столбец (то есть столбца под номером j) матрицы B. В частности, для того, чтобы умножить матрицу A на матрицу B, необходимо, чтобы число элементов в строке матрицы A совпадало с числом элементов в столбцах матрицы B, что означает, что число столбцов первого сомножителя должно совпадать с числом строк второго. В противном случае произведение матриц не существует. При этом число строк произведения AB равно числу строк первой матрицы A, а число столбцов равно числу столбцов второй матрицы B. Так, произведение матрицы A =(aij)2´2 на матрицу B =(bij)2´2 является матрицей C =(cij)2´2 размерности 2´2:
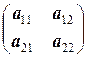
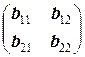 =
= 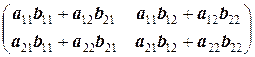 ;
;
а произведение матрицы A =(aij)2´2 на матрицу B =(bij)2´3 является матрицей C =(cij)2´3:
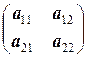
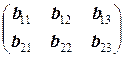 =
= 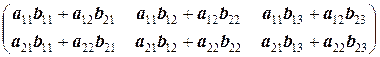 .
.
Произведение B =(bij)2´3 на A =(aij)2´2 не существует, так как число 3 столбцов матрицы B не равно числу 2 строк матрицы A. Например, если A = 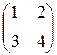 , B =
, B = 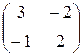 , C =
, C = 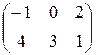 , то
, то
AB = 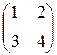
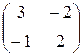 =
= 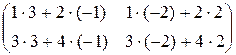 =
= 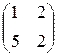 ,
,
BA = 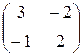
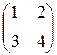 =
= 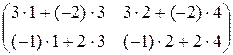 =
= 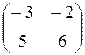 ,
,
AC = 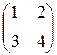
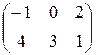 =
= 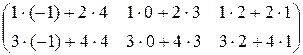 =
= 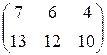 ,
,
CA не определено (то есть не существует).
В частности, мы видим, что, вообще говоря, AB ≠ BA, то есть привычное для чисел правило «от перестановки мест сомножителей призведение не меняется» для матриц не работает.
2.3.3. Теорема. Операция произведения матриц обладает следующими свойствами:
1о. Вообще говоря, AB ≠ BA.
2о. Если произведения AB и BC определены, то определены также произведения (AB) C, A (BC) и при этом выполняется равенство
(AB) C = A (BC).
3о. Am ´ nЕn = ЕmAm ´ n = Am ´ n. В частности, если A - квадратная матрица порядка n, то AЕ = ЕA = A, где E - единичная матрица порядка n.
4о. Если AB определено, то для любого числа a произведения (aA) B, A (aB) также определены и имеют место равенства
a (AB)=(aA) B = A (aB).
5о. Если определено произведение A (B + C), то определены также произведения AB, AC и сумма AB + AC, и справедливо равенство
A (B + C)= AB + AC.
6о. Если определено произведение (A + B) C, то определены также произведения AC, BC и сумма AC + BC, и справедливо равенство
(A + B) C = AC + BC.
7о. Если определено произведение AB, то определено также произведение B T A T и справедливо равенство
(AB)T= B T A T.
2.3.4. Перечисленные свойства естественным образом обобщаются. Например, как и в случае суммы, свойство 2о обобщается следующим образом:
2 ¢ о. Если произведения A 1 A 2, A 2 A 3, …, Ak -1 Ak, определены, то определено также произведение
(…((A 1 A 2) A 3)… Ak -1) Ak (2.2)
и результат произведения не зависит от расстановки скобок.
В силу этого в произведениях типа (2.2) скобки принято опускать:
A 1 A 2… Ak (2.3)
Вообще, в произведении (2.3) определено произведение любого количества l друг за другом идущих матриц: AiAi +1… Ai + l -1. В силу свойства 1о результат произведения зависит от порядка следования сомножителей. Более того, при перестановке сомножителей произведение может быть вообще не определённым (то есть не существовать).
4 ¢ о. Если определено произведение A 1 A 2… Ak, то определены также произведения (aA 1) A 2… Ak, A 1(aA 2)… Ak, A 1 A 2…(aAk), и имеют место равенства
(aA 1) A 2… Ak = A 1(aA 2)… Ak =…= A 1 A 2…(aAk).
5 ¢ о, 6 ¢ о. Если определены произведения A (B 1± B 2±…± Bk) и (A 1± A 2±…± Ak) B, то определены соответственно произведения AB 1, AB 2, …, ABk и A 1 B, A 2 B, …, AkB и имеют место равенства
A (B 1± B 2±…± Bk)= AB 1± AB 2±…± ABk,
(A 1± A 2±…± Ak) B = A 1 B ± A 2 B ±…± AkB.
Здесь сочетания знаков «+» и «-» произвольные.
7 ¢ о. Если произведение A 1 A 2… Ak -1 Ak определено, то определено также произведение 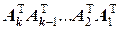 и при этом имеет место равенство
и при этом имеет место равенство
(A 1 A 2… Ak -1 Ak)Т= 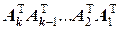 .
.
2.3.5. Определение. Если A - квадратная матрица, то произведение 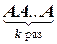 называется k - й степенью матрицы A и обозначается через Ak:
называется k - й степенью матрицы A и обозначается через Ak:
Ak = 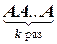 .
.
 2015-03-08
2015-03-08 5129
5129
