Корреляционный момент и коэффициент корреляции

• Корреляция
• Корреляционный момент и коэффициент корреляции
• Коррелированность и зависимость случайных величин
• Нормальный закон распределения на плоскости
• Линейная регрессия. Прямые линии среднеквадратической регрессии
• Линейная корреляция. Нормальная корреляция
• Коэффициент корреляции Пирсона
• Коэффициент корреляции Пирсона: пример решения задачи
• Коэффициент ранговой корреляции Спирмена
• Коэффициент корреляции Спирмена: пример решения задачи

Случайная величина описывается двумя числовыми характеристиками: математическим ожиданием и дисперсией. Чтобы описать систему из двух случайных величин кроме «основных» характеристик используют так же корреляционный момент и коэффициент корреляции.
Корреляционным моментом µ_xy случайных величин X и У называют математическое ожидание произведения отклонений этих величин:

µ_xy = M { [ X - M(X) ] [ Y - M(Y) ] }

Для нахождения корреляционного момента дискретных величин используют формулу:

,

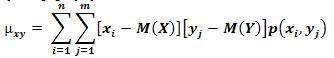а для непрерывных величин — формулу:

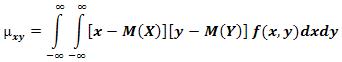
Корреляционный момент характеризует наличие (отсутствие) связи между величинами X и У. Ниже будет доказано, что корреляционный момент равен нулю, если X и У независимы; Если же корреляционный момент для случайных величин X и Y не равен нулю, то между ними имеется зависимость.

Коэффициентом корреляции г_ху случайных величин X и У называют отношение корреляционного момента к произведению средних квадратических отклонений этих
величин: r_xy= µ_xy/σ_xσ_y