Задачи 51-60. Вычислить приближенное значение , заменяя приращение функции дифференциалом, если n = 6

Вычислить приближенное значение 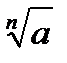, заменяя приращение функции 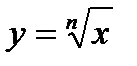дифференциалом, если n = 6,

а =60.

Решение: Нужно вычислить приближенно .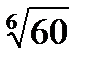

Приращение функции в точке : .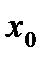

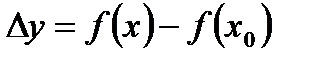Дифференциал функции в точке : .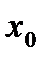

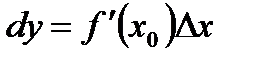При малых 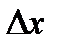: 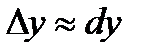или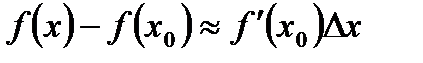

Отсюда получаем общую формулу для приближенных вычисле­ний: 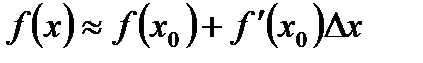, где .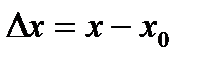

В нашей задач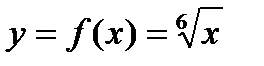е , где .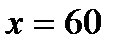

Найдем производную функции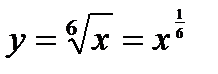

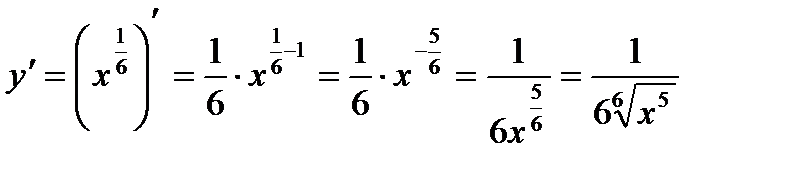
Приближенное равенство для функции 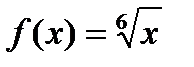будет иметь вид:

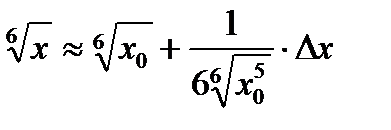
Здесь 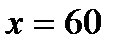, в качестве 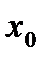выберем число 64, оно ближайшее 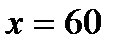, из которого точно извлекается корень шестой степени: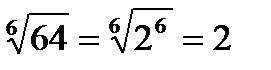

Следовательно, 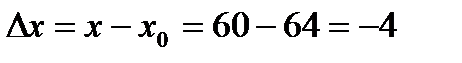. Подстав­ляя в последнюю приближенную формулу 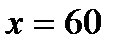, , 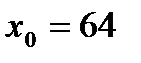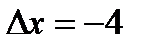най­дем нужный результат:

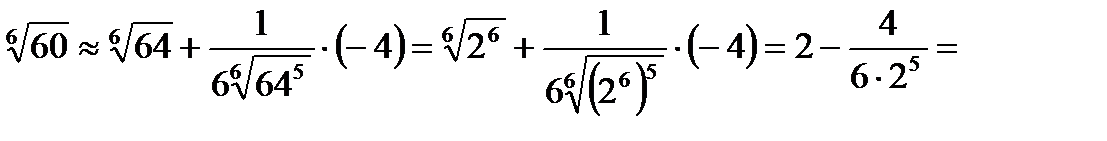
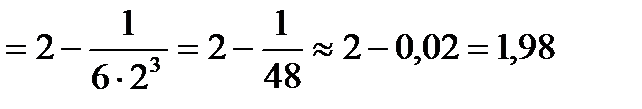
Ответ: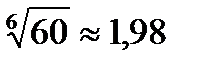

Задачи 61-70 относятся к теме "Функции нескольких переменных". Для решения этих задач необходимо познакомиться со следующими вопросами названной темы:

1. Определение функции двух переменных, область определения функции, геометрическое изображение функции двух переменных.

2. Определение частных производных первого порядка для функции двух переменных, их вычисление.

3. Полный дифференциал функции двух переменных.

4. Производные высших порядков для функции двух переменных.

5. Определение локальных экстремумов для функции двух переменных.

6. Необходимое и достаточное условия экстремума для функции двух переменных.

7. Правило исследования на экстремум для функции двух переменных.