2015-05-14
1431
Теперь рассмотрим содержание понятия гарантированного уровня выигрыша. Поскольку: рассматриваем матричную игру с нулевой суммой, то первый игрок старается (заинтересованный) выбрать такую стратегию (которая отвечает выбору определенной строки матрицы платежей), при которой величина функции платежей hij достигает наиболее возможного значения. Партнер, действует так, чтобы эта величина достигла по возможности меньшее значение (выбор соответственного столбца матрицы платежей).
Но значение hij зависит от выбора номера как строки, так и столбца. Этот выбор выполняется разными участниками игры с противоположными целями. Первый игрок, выбрав і-тую стратегию, может достичь лишь того, что его партнер позволит ему иметь наименьший выигрыш среди всех возможных по выбранной і-й стратегии. Нижним гарантированным уровнем выигрыша aі первого игрока будет величина
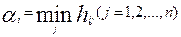
Естественно, что первый игрок будет выбирать такую i-тую стратегию, по которой он вероятно получит какой-либо максимально возможный выигрыш, то есть выбор стратегии первого игрока определяется условием
|
|
|
:
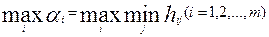Наибольший гарантированный выигрыш h (1) первого игрока определяется так:
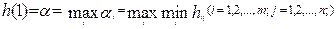
Оптимальной стратегией первого игрока будет та, для которой выполняется условие (1), то есть стратегия, по которой нижний гарантированный уровень достигает наибольшего значения по имеющейся матрице выигрышей.
Противоположная сторона модели конфликтной ситуации - второй игрок, учитывая, что игра есть с нулевой суммой, стремится, чтобы его проигрыш был наименьшим, итак, его оптимальной стратегией будет выбор такого столбца матрицы платежей, для которого величина платежа h2 (величина его проигрыша) будет наименьшей среди всех наибольших платежей, которых стремится достичь первый игрок.
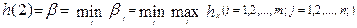
Оптимальная стратегия первого игрока называется максиминной. При такой стратегии его выигрыш при любом противодействии партнера будет не меньше величины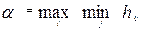 
, которую называют нижней ценой игры. Оптимальная стратегия второго игрока называется минимаксной, а величина его проигрыша по такой стратегии определяется величиной 
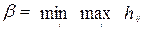- верхней ценой игры. Целесообразно подчеркнуть, что величины h(1), a, h(2) и b имеют разное содержание и, как будет показано дальше, не всегда совпадают численно.
В случае, когда величины нижней и верхней цены игры совпадают, такую величину называют чистой ценой игры, или ценой игры; при таких условиях величина выигрыша первого игрока равняется величине проигрыша второго игрока. Чистой стратегией игрока называют выбор минимаксной стратегии в матрице платежей. Итак, когда нижняя и верхняя границы игры совпадают, то задача имеет решение в чистых стратегиях, игра называется игрой с седловой точкой. Седловой точкой называют пару чистых стратегий, при которых выигрыш равняется цене игры.
|
|
|
Седловая точка в решении задачи имеет такое значение: если один из игроков избрал стратегию, которая отвечает седловой точке, то у партнера нет лучшего выбора, чем выбор той своей стратегии, которая отвечает седловой точке. Для стратегий iojo, которые порождают седловую точку, справедливо отношение:
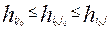
(и,j - любые чистые стратегии игроков).
В соответствии с (3) элемент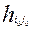 
матрицы платежей есть наименьшим в і0-й строке и наибольшим в j0-ом столбце (не больше любого элемента і0-й строки и не меньше любого элемента j0-го столбца).
Поиск седловой точки выполняется так. В матрице платежей поочередно (последовательно) в каждой строке находят минимальный элемент. Если такой элемент и вдобавок будет максимальной для своего столбца, то он называется седловым элементом, а стратегии, которые его порождают, определяют седловую точку. Чистые стратегии, которые определяют седловую точку, называются оптимальными чистыми стратегиями. Смысл игры с нулевой суммой - в определении оптимальных чистых стратегий и соответствующего элемента 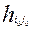матрицы платежей, если это можно выполнить по известной матрице платежей.
Замечание. Игра (матрица платежей) может иметь несколько седловых точек.
Пример. Найти решение игры, определенной такой матрицей платежей (табл. 14.1).
Таблица 14.1.
| Bj Ai | aі(min) | ||||
| -4 | -4 | ||||
| -1 | -5 | -5 | |||
| bj(тах) |
Рассматриваем поочередно строки матрицы и находим в каждой строке минимальный элемент aи, записываем его величины в крайний правый столбец табл. 14.1. Для первой строки наименьший элемент ai = a1,4 = -4 не может быть седловым, так как он не является наибольшим в четвертом столбце.
Для второй строки минимальное значение выигрыша a2 = 2 может быть достигнуто при условии, что партнер выберет или первую, или четвертую стратегию, но величина 2 является наибольшей для первого и четвертого столбцов, а это означает, что элементы h2,1и h2,4 - седловые и создают решение:
- оптимальная стратегия первого игрока - вторая; партнер имеет за этого условия две оптимальных стратегии - первую и четвертую;
- цена моделированной игры равняется 2.
Проанализировав третью строку матрицы выигрышей табл. 14.1, необходимо убедиться, что эта строка не может иметь седловых элементов. Итак, игра с представленной в табл. 14.1 матрицей выигрышей имеет две седловые точки в чистых стратегиях h2,1и h2,4; оптимальные стратегии названы выше.
Опыт моделирования оконченных антагонистических игр показывает, что решение в чистых стратегиях - это исключение, а не закономерность. Рассмотрим модели игр при отсутствии седловых точек.
Проанализируем возможный ход игры с матрицей платежей
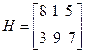
учитывая тот факт, что при известной матрице платежей неизвестно, какие стратегии выберут игроки. Выполним оценку возможного выигрыша (проигрыша) игроков. Если игрок А выберет первую стратегию, надеясь, что она будет самой плохой, если игрок выберет свою вторую стратегию, при которой его проигрыш будет равняться 1, то соответственно выигрыш игрока А тоже будет равняться 1. Но игрок В, анализируя матрицу Н, ожидает от игрока А выбора второй стратегии, так как при таком выборе игрок А будет иметь самый минимальный выигрыш 3. Если игрок В выберет первую стратегию, при других стратегиях игрока В выигрыш А будет только увеличен. Для игрока В выбор первой стратегии рискованный, так как если игрок А уже выбрал свою первую стратегию, то игрок В проиграет 8.
Вопрос выбора игроками своих наилучших стратегий по алгоритмом, описанным в 14.3, не может быть решено однозначно. Другими словами, модель игры по приведенной матрице Н не имеет решений в чистых стратегиях. В такой ситуации становится важным чтобы неприятель не угадал, какая стратегия будет использована.
|
|
|
В общем случае в играх, которые моделируют конфликтные ситуации, нижняя и верхняя цены игры, как правило, не совпадают; решение таких задач не может быть найден в чистых стратегиях. Возникает вопрос: существует ли решение при таких условиях, как его найти, если оно есть?
Если игрок А, выполнив анализ матрицы платежей, воспользуется своей максиминной стратегией, то он будет иметь выигрыш не меньшее a (нижней цены игры) (1) Игрок В по своей минимаксной стратегии будет иметь проигрыш не больший b (верхней цены игры) (2). Промежуток [a; b] - это область неопределенности, в границах которой игрок А имеет определенную вероятность увеличить свой выигрыш, а игрок В - уменьшить проигрыш.
То есть по приведенной матрице выигрышей (4) нет возможности однозначно определить каждому игроку свои стратегии.
Если исследуемая игра одноразовая, то теоретически игрок А не имеет возможности увеличить выигрыш, если не рисковать. Совсем другой будет ситуация, если игра повторяется многократно; при этих условиях можно увеличить средний гарантированный выигрыш игрока А за счет определенной случайной комбинации чистых стратегий [[i] ].
Рассмотрим некоторые особенности решения матричных игр. Подчеркнем, что в оптимальной смешанной стратегии некоторые возможные чистые стратегии игроков могут быть и не использованными при условии, что вероятности таких чистых стратегий равняются нулю.
Активными называются такие чистые стратегии игрока, которые входят в оптимальную стратегию с вероятностями, отличными от нуля.
Поиск оптимальных стратегий существенно усложняется, если размеры матрицы платежей возрастают. Рассмотрим условия, которые позволяют уменьшить размерность матрицы платежей, не нарушая решения задачи.
Ряды (строки или столбцы) матрицы платежей называются дублирующими, если их элементы тождественны. Для расчетов оставляют только один из дублированных рядов.
|
|
|
В теории матричных игр доказано, что если элементы одной строки не меньше соответствующих элементов второй строки, то в оптимальную смешанную стратегию могут быть введенные только стратегии доминирующих строк, то есть строки, над которыми есть доминирующие, можно изъять.
Для игрока, который контролирует величину своего возможного проигрыша, наверное, нецелесообразными являются те стратегии, величины проигрышей по которым больше, чем по его другим стратегиям и по любым стратегиям игрока А. Поэтому, если в матрице платежей есть столбцы, элементы которых не меньше элементов других столбцов, такие столбцы целесообразно опустить (игроку В, наверное, нецелесообразно пользоваться соответствующими стратегиями).
Вероятностями чистых стратегий, номера которых отвечают номерам опущенных рядов матрицы платежей, необходимо присвоить нулевые значения.
Пример. Имеем матрицу платежей
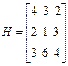
в которой третья строка доминирует над второй. Изымем вторую строку:
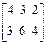
В полученной матрице второй столбец доминирует над третьим. Изъяв второй столбец, получаем матрицу платежей
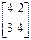
Если найти решение игры для полученной матрицы, то его легко использовать для построения решения игры с исходной матрицей Н, присвоив номерам стратегий, которые отвечают номерам изъятых рядов, нулевые значения.
Второй способ упрощения матрицы выигрышей основывается на доказанном в теории игры свойстве, при котором афинное преобразование матрицы платежей (то есть преобразование (перерасчет) всех элементов матрицы Н по правилу hHij = ah ij + b, где а ¹ 0) не изменяет решений игры, и вдобавок цена VH игры с превращенной матрицей равняется a + b. Приведенное свойство означает, что для построения матрицы платежей не имеет значения, в каких единицах измеряются выигрыши (проигрыши), а добавление (отнимание) определенной величины b на такую же величину изменит выигрыш (проигрыш), не изменив решение игры.
Напомним, что под решением игры понимают упорядоченную совокупность вероятностей использования определенных чистых стратегий. Величина выигрыша (проигрыша) будет зависеть от единицы измерения элементов матрицы платежей.
Афинное преобразование матрицы платежей целесообразно использовать для ее упрощения: если в клетках матрицы есть дроби с общим знаменателем, то всю матрицу можно помножить на некоторую постоянную величину, чтобы получить целые числа; если многие элементы матрицы являются тождественными, то их величину можно отнять от элементов всей матрицы, чтобы иметь нули на соответствующих позициях. И вдобавок любую антагонистическую игру можно перевести в класс справедливых - для этого необходимо от каждого элемента исходной матрицы платежей отнять цену игры. Но следует помнить, что, найдя решение, надо возвратиться к содержанию исходной задачи.
Пример. Должны заложить сад, пользуясь двумя видами фруктовых деревьев, при условии, что плотность деревьев на единицу площади одинаковая, а чистая выгода через определенное время от любого дерева на единицу затрат ежегодно будет определяться в зависимости от условий эксплуатации (табл. 14.2). Под неблагоприятными условиями следует понимать не только естественные, а и уровень ухода в зависимости от материально-технических возможностей. Неблагоприятные условия будем рассматривать как противодействующего игрока, подчеркнув, что неблагоприятные условия для одного вида деревьев могут быть благоприятными для другого.
Таблица 14.2.
| Условия Вид дерева | Благоприятные | Неблагоприятные |
| 0,7 | 0,4 | |
| 0,3 | 0,6 |
Выпишем матрицу выигрышей:
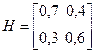
Воспользовавшись возможностями афинных преобразований, помножим все элементы матрицы на 10 и запишем в виде:
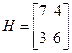
Исследуем задачу на поиск решения в чистых стратегиях, то есть целесообразности
воспользоваться только одним видом деревьев. Величина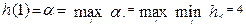 
, величина 
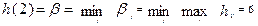. Нижняя и верхняя цены игры не совпадают, решения в чистых стратегиях нет. Итак, решение необходимо искать в смешанных стратегиях, то есть искать оптимальное соотношение между количествами деревьев первого и второго видов, рассматривая такое соотношение как случайную величину. Посадку деревьев первого вида будем считать за первую стратегию, деревьев второго вида - за вторую стратегию. Обозначим р случайную часть деревьев первого вида, тогда доля деревьев второго вида будет составлять q = 1 - р, а средняя ожидаемая выгода Н1с (математическое ожидание величины выгоды) при благоприятных условиях будет равняться:
Н1с =7p + 3(1-p) = 4p+3; (8)
средняя ожидаемая выгода при неблагоприятных условиях Н1Н:
Н1Н =4p + 6(1-p) = -2p+6. (9)
Выберем прямоугольную систему координат (р, Н1) и построим в ней графики (8), (9), избрав определенный масштаб.
Любой из графиков будет изображен отрезками прямой, которые пересекаются в точке Т. Обозначим отрезки А1А'1 и А2А'2. Если первый игрок (садовник) выберет определенную величину р (долю деревьев первого вида), то при благоприятных условиях (первая стратегия "партнера") его ожидаемый средний выигрыш (выгода) будет изображен точкой Н1с пересечения прямой р с отрезком А1А'1, при неблагоприятных условиях - точкой пересечения Н1Н этой же прямой с отрезком А2А'2. Промежуточные значения величины средней ожидаемой выгоды расположены между точками Н1с и Н1Н. На эти значения можно надеяться, если "партнер" будет пользоваться смешанными стратегиями (определенное соотношение благоприятных и неблагоприятных условий). Но первый игрок (садовник) стремится иметь наибольшую, но гарантированную выгоду, величина которой на рис 14.2 достигается в точке Т при условии, что р = 0,5. За других величин р наибольшая гарантированная выгода графически будет изображаться точками отрезку А1ТА'2. Практический вывод: при данных условиях задачи целесообразно высадить поровну деревья первого и второго видов.
Наибольшая гарантированная выгода при этих условиях будет при р = 0,5. Предлагаем доказать, что поставленная задача дает решение р = 0,75 при условии, что матрица Н имеет вид:
.
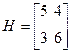Следует дать толкования решению.
Для построения алгоритмов решения задач матричных игр используется свойство оптимальных смешанных стратегий: оптимальная смешанная стратегия первого игрока гарантирует ему выигрыш не меньше цены игры по любым стратегиям второго игрока и равный цене игры по оптимальной стратегии второго игрока. Использование названного свойства матричных игр дает возможность привести задачу поиску оптимальных смешанных стратегий к задаче линейного программирования. Одна из методик построения соответствующего алгоритма рассмотренна в [[ii] ].
Пример. Предприятие может выпускать четыре вида продукции А1, А2, А3, А4, получая прибыль в зависимости от спроса, который условно может быть определен тремя разными состояниями B1, B2, B3. Построим матрицу выигрышей Н, элементы которой hij определяют прибыль предприятия при условии выпуска і-ой продукции при j-м спросе на нее.
| В1 | В2 | В3 | ||
| Н= | А1 |  3
| ||
| А2 | ||||
| А3 | ||||
| А4 |
Определить оптимальные пропорции в производстве продукции, которые бы гарантировали некоторую среднюю величину прибыли при любом спросе, считая ее неопределенной.
Проанализировав матрицы, приходим к выводу, что третья строка доминирует над четвертой, поэтому для дальнейшего четвертую строку изымем. Экономически это означает нецелесообразность производства продукции четвертого вида при данных условиях. Решение задачи построим как исследование модели игры производителя с неизвестными условиями спроса.
Определим верхнюю и нижнюю цены игры. Расчеты приведены в табл. 14.3.
Таблица 14.3.
| Спрос Вид продукции | В1 | В2 | В3 |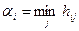 
|
| А1 | ||||
| А2 | ||||
| А3 | ||||
|
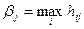Поскольку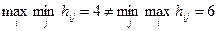 
, то задача не имеет решения в чистых стратегиях и оптимальное решение будем искать в смешанных стратегиях:
, 
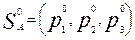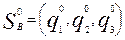
Введем новые переменные хі = pі0/V (і = 1,2, 3) и yi = qj0/V (j =1,2, 3). Используя зависимости (12), (13) и (16), (18), запишем две сопряженные задачи линейного программирования:
| задача 1 | задача 2 | ||
| 3х1 + 9х2 + 7х3 ³ 1 6х1 + 4х2 + 5х3 ³ 1 8х1 + 2х2 + 4х3 ³ 1 х1 ³ 1; и = 1,2,3 Z = х1 + х2 + х3®min | 3y1 + 6y2 + 8y3 £ 1 9y1 + 4y2 + 2y3 £ 1 7y1 + 5y2 + 4y3 £ 1 y1£ 1; j = 1,2,3 Z* = y1 + y2 + y3®max |
Решим симплексом-методом с помощью ПК.
Оптимальным решением задачи 1 Î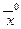 
= (2/27; 0; 1/9; 0; 0; 1/27), а min Z = maxZ* = 5/27. Воспользовавшись (17), вычисляем цену игры V = 1/max Z* = 1/min Z = 27/5 = 5,4.
При решении задач оконченных игр размерности т х п целесообразно придерживаться такой схемы:
1) исключить из исходной платежной матрицы явным образом невыгодные стратегии;
2) найти верхнюю и нижнюю цены игры и проверить, имеет ли игра седловую точку. Если такая точка есть, то соответствующие ей стратегии будут оптимальными, игра имеет решение в чистых стратегиях, а цена игры равняется верхней (нижней) цене;
3) если седловая точка отсутствует, решение игры необходимо искать в смешанных стратегиях, приводя, например, к задаче линейного программирования.
На практике решение в смешанных стратегиях может быть реализовано по-разному. Например, чистые стратегии используются в последовательности, заданной соответствующими вероятностями при условии, что игра может повторяться много раз. При других условиях выполняется определенное физическое распределение в пропорциях, определенных вероятностями, как это было показано на примерах планирования сада и производства.
Пример. 1. Рассмотрим задачу о поставке сырья. Предположим, что некоторая фирма А заключила договор с другой фирмой В на поставку сырья, которое быстро портится, ежедневно на сумму 100 у.е. Если в течение дня сырье не поступает, фирма А несет убытки в размере 400 у.е. от простоя рабочих. Она может использовать свой транспорт (дополнительные затраты 50 у.е.), но опыт показывает, что в половине случаев транспорт возвращается пустым. Можно увеличить вероятность получения сырья до 80%, если предварительно посылать на фирму В своего представителя, но это требует дополнительных затрат в размере 40 у.е. Существует возможность заказать дневную норму сырья в другой фирме по цене, на 50% выше, но кроме затрат на транспорт (50 у.е.) возможны дополнительные затраты в размере 30 у.е., связанные с ненормированной работой бригад, которые реализуют лишнее сырье, если в тот же день поступает и централизованная поставка. Какой стратегии должна придерживаться фирма А, если заранее неизвестно, поступит или не поступит централизованная поставка сырья?
Для решения задачи прежде всего приведем возможные стратегии поставщика (фирма В):
B1 - поставка своевременна;
В2 - поставки нет.
У фирмы А, в соответствии с условием задачи, четыре стратегии:
A1 - не принимать никакие дополнительные меры;
А2 - послать на фирму В свой транспорт;
А3 - послать на фирму В своего представителя и транспорт;
А4 - заказать дополнительное сырье на другой фирме.
Всего возможных 8 ситуаций, которые описывают все комбинации с четверых стратегий фирмы А и двух стратегий фирмы В. Эти ситуации и сопутствующие им убытки и затраты приведены в табл. 4.1.
В общем случае, если у первого игрока (фирма А) т возможных стратегий, а у второго - n, то всегда создается т х п возможных ситуаций, каждой из которых отвечает определенный платеж одного игрока второму.
При большом количестве ситуаций табл. 4.1 становится громоздкой и необъятной, удобней перейти от нее к платежной матрице А. Она является прямоугольной матрицей, которая имеет т строк (по количеству стратегий первого игрока) и п столбиков (по количеству стратегий второго игрока).
Таблица 4.1
