Задание 1.1.2.1. ОАО «ЮВЖД» вынуждено периодически повышать цены на свои услуги. То, что повышение цен явно негативным образом влияет на число пассажиров, пользующихся услугами железной дороги, можно понять, проанализировав, в частности, данные табл. 1.1.2.1.
Т а б л и ц а 1.1.2.1
| Стоимость проезда 1 чел. в поезде Воронеж - Москва, руб. | Среднемесячное число пассажиров поезда Воронеж-Москва | Стоимость проезда 1 чел. в поезде Воронеж - Москва, руб. | Среднемесячное число пассажиров поезда Воронеж-Москва |
Несмотря на это, руководство «ЮВЖД» планирует в следующем периоде поднять цены на билеты для пассажиров поезда Воронеж – Москва. В связи с этим было решено поручить студенту экономического факультета, проходящего практику в отделе экономического анализа управления юго-восточной железной дороги, известным ему методом спрогнозировать среднемесячное число пассажиров поезда при условии, что билет на этот поезд будет стоить 690 руб. Студент-практикант решил применить к имеющимся данным регрессионный анализ и, воспользовавшись его результатами, получить требуемую прогнозную оценку.
Решение с помощью MS Excel
1. Ввод исходных данных.
2. Подготовка данных для расчета оценок коэффициентов линейной регрессии и оформление их в виде табл. 1.1.2.2.
Т а б л и ц а 1.1.2.2
| № п.п. | 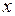 | 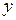 | 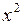 | 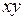 | 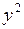 |
| 1. | |||||
| 2. | |||||
| 3. | |||||
| 4. | |||||
| 5. | |||||
| 6. | |||||
| 7. | |||||
| 8. | |||||
| 9. | |||||
| 10. | |||||
| 11. | |||||
| 12. | |||||
| 13. | |||||
| 14. | |||||
| 15. | |||||
| 16. | |||||
| Средние значения | 416,88 | 10918,13 | 205268,75 | 4349625,00 | 120652931,25 |
3. Расчет оценок коэффициентов регрессии
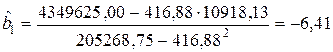 ,
, 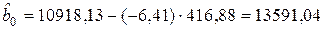 .
.
Таким образом, построенная модель может быть записана в виде
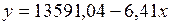 .
.
Коэффициент 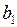 этой модели показывает, что в среднем увеличение стоимости проезда на 1 руб. приводит к уменьшению числа пассажиров на 6 человек.
этой модели показывает, что в среднем увеличение стоимости проезда на 1 руб. приводит к уменьшению числа пассажиров на 6 человек.
4. Расчет коэффициентов корреляции и детерминации
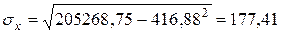 ;
; 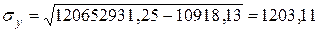 ;
;
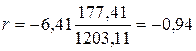 ;
; 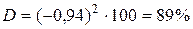 .
.
Коэффициент корреляции достаточно высокий, что свидетельствует о существенной зависимости среднемесячного числа пассажиров от стоимости проезда. Коэффициент детерминации также достаточно высокий, он показывает, что число пассажиров объясняется стоимостью проезда на 89%.
5. Расчет дисперсионного отношения Фишера
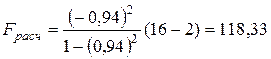 .
.
Сравнение расчетного значения F -критерия с табличным 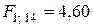 для 95%-го уровня значимости (см. Приложение) позволяет сделать вывод об адекватности построенной модели.
для 95%-го уровня значимости (см. Приложение) позволяет сделать вывод об адекватности построенной модели.
6. Расчет стандартных ошибок по формулам (1.1.1.5), в которых используется средняя квадратическая ошибка 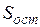 , вычисленная в соответствии с данными табл. 1.1.2.3.
, вычисленная в соответствии с данными табл. 1.1.2.3.
Т а б л и ц а 1.1.2.3
| № п.п. | 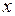 | 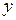 | 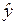 | 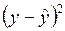 |
| 1. | 12436,92 | 2201,04 | ||
| 2. | 12436,92 | 26596,64 | ||
| 3. | 12116,33 | 42570,52 | ||
| 4. | 12116,33 | 31090,95 | ||
| 5. | 12116,33 | 287645,85 | ||
| 6. | 11378,97 | 123220,91 | ||
| 7. | 11378,97 | 12327,30 | ||
| 8. | 11378,97 | 442,19 | ||
| 9. | 10641,62 | 669750,71 | ||
| 10. | 10641,62 | 135706,02 | ||
| 11. | 10641,62 | 467,30 | ||
| 12. | 9904,26 | 45908,38 | ||
| 13. | 9904,26 | 155442,84 | ||
| 14. | 9198,97 | 450285,72 | ||
| 15. | 9198,97 | 83501,74 | ||
| 16. | 9198,97 | 383119,74 | ||
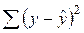 | 2450277,85 | |||
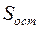 | 418,35 |
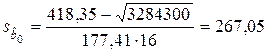 ,
, 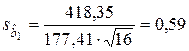 .
.
7. Расчет t -статистик Стьюдента
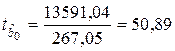 ,
, 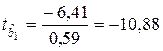 .
.
Сравнение расчетных значений с табличным 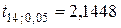 (см. Приложение) подтверждает значимость коэффициентов регрессии.
(см. Приложение) подтверждает значимость коэффициентов регрессии.
8. Расчет доверительных границ для коэффициентов регрессии
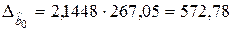 ,
, 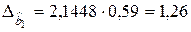 ,
,
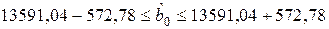 ;
; 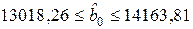 ;
;
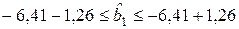 ;
; 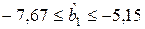 .
.
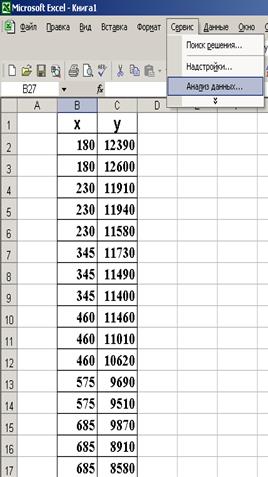
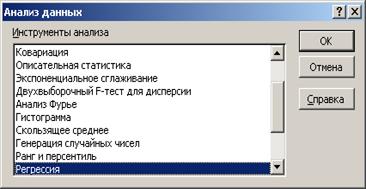
9. Построение линейного уравнения регрессии и расчет всех его характеристик с помощью пакета «Анализ данных» Excel. Для этого сначала необходимо проверить доступ к пакету анализа (см. рис. 1.1.2.1), а затем выполнить действия по построению регрессионного уравнения (см. рис. 1.1.2.2). Результат применения инструмента «Регрессия» представлен на рис. 1.1.2.3.
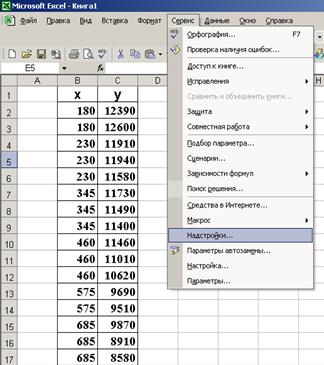 | 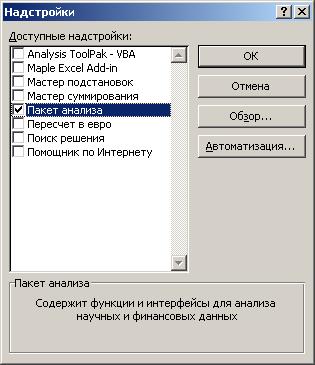 |
Р и с. 1.1.2.1. Подключение надстройки Пакет анализа
10. Получение прогнозной оценки числа пассажиров
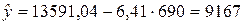 .
.
11. Расчет доверительных границ прогнозной оценки
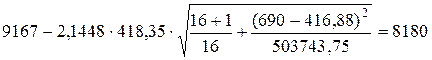 ,
,
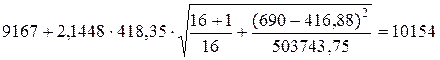 .
.
 |  |
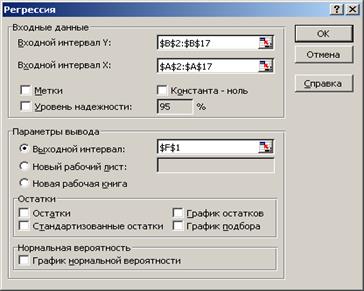 |
Р и с. 1.1.2.2. Построение регрессионного уравнения
с помощью пакета «Анализ данных» MS Excel
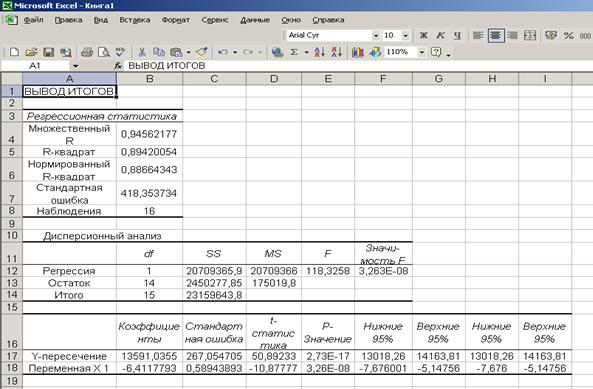
Р и с. 1.1.2.3. Результат применения инструмента «Регрессия»
 2015-05-18
2015-05-18 1022
1022








