Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Т (традиционное обозначение для показательного распределения), которое описывается плотностью 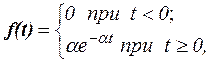 где a – положительная постоянная величина.
где a – положительная постоянная величина.
Функция распределения показательного закона 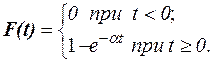
Вероятность попадания показательно распределенной случайной величины Т в промежуток (а; b) 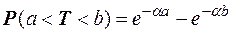 .
.
Числовые характеристики показательно распределенной случайной величины выражаются через её параметр следующим образом: 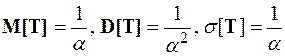 .
.
Связь пуассоновского распределения с показательным выражается в том, что случайная величина Х (число событий некоторого потока за фиксированный промежуток времени t) имеет пуассоновское распределение с параметром l тогда и только тогда, когда случайная величина Т (промежуток времени между последовательными событиями) имеет показательное распределение с параметром a, при этом l = at.
13.1. Найти числовые характеристики показательного распределения, заданного при 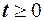 а) плотностью
а) плотностью 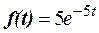 , б) функцией распределения
, б) функцией распределения 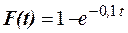 .
.
13.2. Случайная величина Т имеет показательное распределение с параметром a = 2. Найти вероятность попадания Т на промежутки [ 1; 2 ], 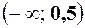 .
.
13.3. Время t расформирования состава через горку – случайная величина, подчиненная показательному закону. Пусть a = 5 – среднее число поездов, которые горка может расформировать за 1 ч. Найти вероятность того, что время расформирования состава: а) меньше 30 мин; б) больше 6 мин, но меньше 24 мин.
13.4 Время безотказной работы технического устройства имеет показательное распределение с параметром a = 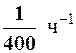 . Найти вероятность того, что устройство проработает безотказно не менее 800 ч.
. Найти вероятность того, что устройство проработает безотказно не менее 800 ч.
13.5. Поток отказов технического устройства с высокой степенью точности моделируется стационарным пуассоновским потоком. Среднее число отказов за 1000 ч работы устройства равно 10. Найти вероятность того, что устройство проработает безотказно не менее 100 и не более 200 ч. Чему равно среднее время безотказной работы технического устройства?
13.6. Испытывают два независимо работающих элемента. Длительность времени безотказной работы первого элемента имеет показательный закон с функцией распределения 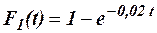 , для второго –
, для второго – 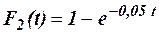 . Найти вероятность того, что за шестичасовой период испытания: а) оба элемента откажут, б) оба элемента не откажут, в) только один элемент откажет, г) хотя бы один элемент откажет.
. Найти вероятность того, что за шестичасовой период испытания: а) оба элемента откажут, б) оба элемента не откажут, в) только один элемент откажет, г) хотя бы один элемент откажет.
13.7. Вероятность обнаружения затонувшего судна за время поиска t задается формулой 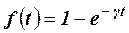 (g > 0). Найти среднее время поиска, необходимое для обнаружения судна.
(g > 0). Найти среднее время поиска, необходимое для обнаружения судна.
13.8. Вероятность безотказной работы ЭВМ имеет экспоненциальное распределение с параметром a = 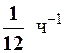 . Найти вероятность того, что за сутки произойдет хотя бы один отказ ЭВМ.
. Найти вероятность того, что за сутки произойдет хотя бы один отказ ЭВМ.
13.9. Длительность времени безотказной работы элемента имеет показательный закон с функцией распределения 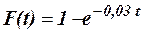 , t ³ 0. Найти вероятность того, что за время длительностью t = 100 ч: а) элемент откажет, б) элемент не откажет.
, t ³ 0. Найти вероятность того, что за время длительностью t = 100 ч: а) элемент откажет, б) элемент не откажет.
 2015-06-10
2015-06-10 3093
3093
