Задача 26 Составить уравнение прямой, которая проходит через точку 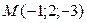 перпендикулярно вектору
перпендикулярно вектору 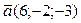 и пересекает прямую
и пересекает прямую 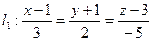 .
.
Решение
Искомая прямая 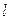 пересекает данную прямую
пересекает данную прямую 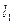 , значит, через них проходит плоскость
, значит, через них проходит плоскость 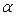 . Найдём нормальный вектор плоскости
. Найдём нормальный вектор плоскости 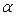 .
.
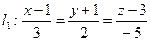 ,
, 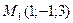 ,
, 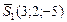
Нормальный вектор плоскости будет перпендикулярен 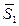 , т.к.
, т.к. 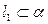 и вектору
и вектору 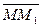 , т.е.
, т.е. 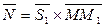 .
.
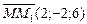
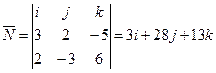
Направляющий вектор искомой прямой 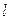 перпендикулярен вектору
перпендикулярен вектору 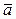 по условию и вектору
по условию и вектору 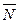 , т.к.
, т.к. 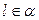 , тогда:
, тогда:
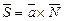 ,
,
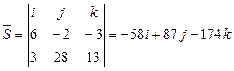 ,
,
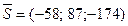 .
.
Составим канонические уравнения прямой 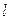 :
:
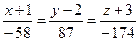
умножим полученное на (–29):
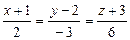
Ответ: 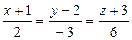
Задача 27 Написать уравнение плоскости, проходящей через точку 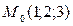 , перпендикулярной плоскости
, перпендикулярной плоскости 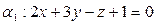 и параллельной прямой
и параллельной прямой 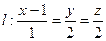 .
.
Решение
Уравнение искомой плоскости 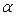 будем искать по формуле:
будем искать по формуле: 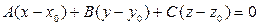 (*), где
(*), где 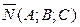
По условию 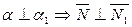 ,
, 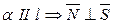 , значит
, значит 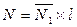
Из уравнения плоскости 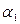 имеем
имеем 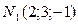 , из уравнения прямой
, из уравнения прямой 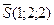 .
.
Тогда
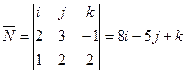 ,
,
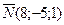 .
.
Подставим координаты вектора 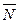 и точки
и точки 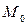 в уравнение (*).
в уравнение (*).
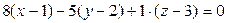 или
или
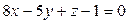
Ответ: 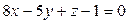
Задача 28 Найти расстояние между скрещивающимися прямыми:
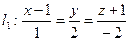 ,
, 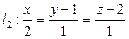 .
.
Решение
Расстояние между скрещивающимися прямыми найдём как расстояние от точки 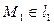 ,
, 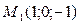 до плоскости
до плоскости 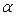 , проходящей через прямую
, проходящей через прямую 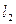 параллельно прямой
параллельно прямой 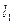 .
.
Уравнение плоскости 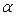 составим по формуле:
составим по формуле: 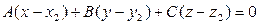 (*).
(*).
Вектор 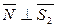 , т.к.
, т.к. 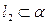 ,
, 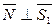 , т.к.
, т.к. 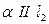 , тогда
, тогда 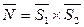 .
.
Из уравнения прямой 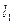 имеем:
имеем: 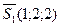 , аналогично
, аналогично 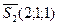 .
.
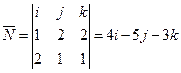
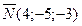
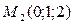 подставим в уравнение (*) координаты вектора
подставим в уравнение (*) координаты вектора 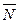 и точки
и точки 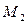 .
.
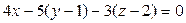
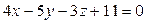
Найдём 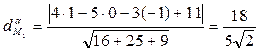
Ответ: 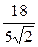
 2015-06-28
2015-06-28 1596
1596