5.20. Что такое пространство 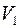 ?
?
5.21. Пусть ненулевой вектор 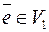 . Как выражается через него любой вектор
. Как выражается через него любой вектор 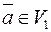 ? Единственно ли данное представление вектора? Поясните термины: базис пространства
? Единственно ли данное представление вектора? Поясните термины: базис пространства 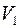 ; координата вектора
; координата вектора 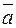 в этом базисе; разложение вектора
в этом базисе; разложение вектора 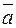 по базису; размерность пространства
по базису; размерность пространства 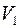 .
.
5.22. Пусть векторы 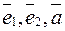 - компланарны, а векторы
- компланарны, а векторы 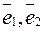 - неколлинеарны. Как, используя линейные операции, выразить вектор
- неколлинеарны. Как, используя линейные операции, выразить вектор 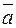 через векторы
через векторы 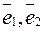 ? Поясните это геометрически. Единственно ли такое представление? Обязательно ли требование неколлинеарности векторов
? Поясните это геометрически. Единственно ли такое представление? Обязательно ли требование неколлинеарности векторов 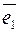 и
и 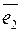 ?
?
5.23. Что такое пространство 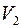 ?
?
5.24. Пусть ненулевые неколлинеарные векторы 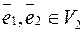 . Как выражается через них любой вектор
. Как выражается через них любой вектор 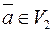 ? Единственно ли данное представление вектора? Поясните термины: базис пространства
? Единственно ли данное представление вектора? Поясните термины: базис пространства 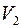 ; координаты вектора
; координаты вектора 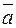 в этом базисе; разложение вектора
в этом базисе; разложение вектора 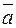 по базису; размерность пространства
по базису; размерность пространства 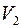 .
.
5.25. Что такое пространство 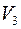 ?
?
5.26. Пусть векторы 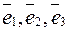 - некомпланарны. Как, используя линейные операции, выразить любой вектор
- некомпланарны. Как, используя линейные операции, выразить любой вектор 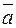 через векторы
через векторы 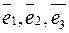 ? Поясните это геометрически. Единственно ли такое представление? Обязательно ли требование некомпланарности векторов
? Поясните это геометрически. Единственно ли такое представление? Обязательно ли требование некомпланарности векторов 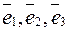 ?
?
5.27. Пусть ненулевые некомпланарные векторы 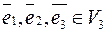 . Как выражается через них любой вектор
. Как выражается через них любой вектор 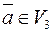 ? Единственно ли данное представление вектора? Поясните термины: базис пространства
? Единственно ли данное представление вектора? Поясните термины: базис пространства 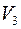 ; координаты вектора
; координаты вектора 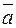 в этом базисе; разложение вектора
в этом базисе; разложение вектора 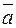 по базису; размерность пространства
по базису; размерность пространства 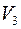 .
.
5.28. Дайте определения линейной зависимости и линейной независимости системы векторов.
5.29. Являются ли линейно зависимыми или линейно независимыми следующие системы векторов: а) два коллинеарных вектора; б) два неколлинеарных вектора; в) три компланарных вектора; г) три некомпланарных вектора; д) четыре некомпланарых вектора; е) базисы пространств 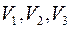 ?
?
5.30. Пусть известны координаты векторов 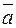 и
и 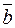 в некотором базисе. Как найти координаты вектора
в некотором базисе. Как найти координаты вектора 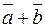 ?
?
5.31. Пусть известны координаты вектора 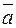 в некотором базисе и число
в некотором базисе и число 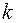 . Как найти координаты вектора
. Как найти координаты вектора 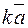 ?
?
5.32. Пусть в некотором базисе заданы векторы 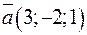 и
и 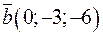 . Найдите координаты вектора
. Найдите координаты вектора 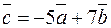 .
.
5.33. Как, зная координаты двух векторов в некотором базисе, определить, являются ли эти векторы коллинеарными? Коллинеарны ли векторы:
а) 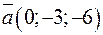 и
и 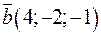 ; б)
; б) 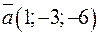 и
и 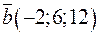
5.34. Пусть в некотором базисе 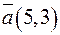 ,
, 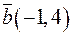 ,
, 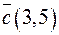 . Определите, образуют ли векторы
. Определите, образуют ли векторы 
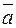 и
и 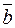 базис в пространстве
базис в пространстве 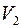 . Если да, то разложите вектор
. Если да, то разложите вектор 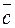 по этому базису.
по этому базису.
5.35. Что такое прямоугольный (ортонормированный) базис?
5.36. Запишите координаты вектора 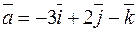 . Пусть в ортонормированном базисе
. Пусть в ортонормированном базисе 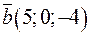 . Запишите разложение вектора
. Запишите разложение вектора 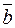 по этому базису.
по этому базису.
5.37. Запишите координаты векторов 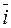 ,
, 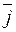 и
и 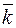 .
.
5.38. Пусть 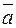 ,
, 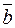 и
и 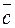 - векторы из задания 5.32. Найдите координаты вектора
- векторы из задания 5.32. Найдите координаты вектора 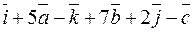
5.39. Как «устроена» прямоугольная декартова система координат? Как определяются координаты точки в этой системе координат? Укажите вектор, координаты которого совпадают с декатровыми координатами точки 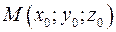 .
.
5.40. Пусть в декартовой прямоугольной системе координат 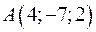 ,
, 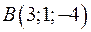 , а точка
, а точка 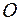 - начало координат. Найдите координаты векторов
- начало координат. Найдите координаты векторов 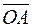 ,
, 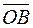 и
и 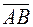
5.41. Как найти координаты вектора по координатам его начала и конца?
5.42. Даны координаты вершин треугольника: 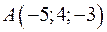 ,
, 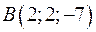 ,
, 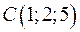 . Найдите координаты векторов
. Найдите координаты векторов 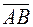 ,
, 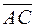 и
и 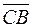 .
.
5.43. Известны координаты трех вершин параллелограмма: 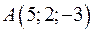 ,
, 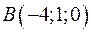 , и
, и 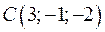 . Найдите координаты четвертой вершины
. Найдите координаты четвертой вершины 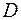 и координаты векторов
и координаты векторов 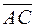 ,
, 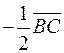 ,
, 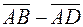 .
.
5.44. Пусть 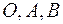 - точки в пространстве, точка
- точки в пространстве, точка 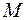 - середина отрезка
- середина отрезка 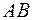 . Выразите вектор
. Выразите вектор 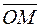 , где через векторы
, где через векторы 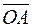 и
и 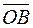 .
.
5.45. Пусть 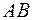 и
и 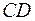 - отрезки в пространстве, а точки
- отрезки в пространстве, а точки 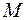 и
и 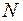 - их середины соответственно. Выразите вектор
- их середины соответственно. Выразите вектор 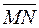 через векторы
через векторы 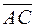 и
и 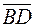 .
.
5.46. Пусть 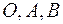 - точки в пространстве, а точка
- точки в пространстве, а точка 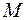 делит отрезок
делит отрезок 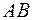 в отношении
в отношении  , считая от точки
, считая от точки 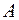 . Выразите вектор
. Выразите вектор 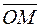 , где через векторы
, где через векторы 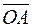 и
и 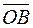 .
.
5.47. Пусть 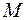 - середина отрезка
- середина отрезка 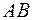 . Выразите координаты
. Выразите координаты 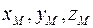 точки
точки 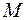 через координаты точек
через координаты точек 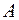 и
и 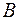 .
.
5.48. Пусть точка 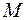 делит отрезок
делит отрезок 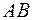 в отношении
в отношении  , считая от точки
, считая от точки 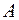 . Выразите координаты
. Выразите координаты 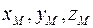 точки
точки 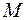 через координаты точек
через координаты точек 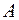 и
и 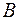 .
.
5.49. 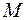 - точка пресечения медиан треугольника
- точка пресечения медиан треугольника 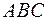 ,
, 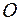 - произвольная точка пространства. Выразите вектор
- произвольная точка пространства. Выразите вектор 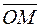 через векторы
через векторы 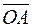 ,
, 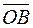 и
и 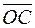 .
.
5.50. Задан тетраэдр 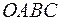 . В базисе из ребер
. В базисе из ребер 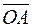 ,
, 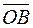 и
и 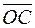 найти координаты:
найти координаты:
а) вектора 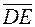 , где
, где 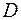 и
и 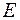 - середины ребер
- середины ребер 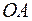 и
и 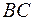 ;
;
б) вектора 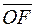 , где
, где 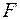 - точка пересечения медиан основания
- точка пересечения медиан основания 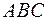
 2015-06-28
2015-06-28 1775
1775