| Потенциал. Разность потенциалов. Напряжение. | |
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: 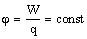 - энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. - энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. | 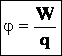 |
| Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора. | |
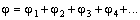 - следствие принципа суперпозиции полей (потенциалы складываются алгебраически). - следствие принципа суперпозиции полей (потенциалы складываются алгебраически). | 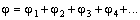 |
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах:  | |
| Разность потенциалов | |
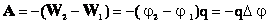 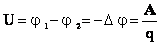 | |
| Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! | 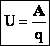 |
Единица разности потенциалов 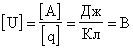 Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. | 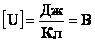 |
| Связь между напряженностью и напряжением . | |
Из доказанного выше: 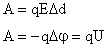 → → 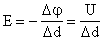 напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d). напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d). | 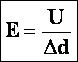 |
Из этого соотношения видно: 1. Вектор напряженности направлен в сторону уменьшения потенциала. 2. Электрическое поле существует, если существует разность потенциалов. 3. Единица напряженности: 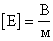 - Напряженность поля равна 1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В. - Напряженность поля равна 1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В. | 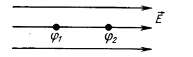 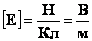 |
| Эквипотенциальные поверхности. ЭПП - поверхности равного потенциала. Свойства ЭПП: - работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; - вектор напряженности перпендикулярен к ЭПП в каждой ее точке. | 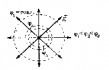  |
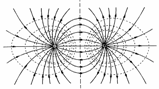 | |
| Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр. | 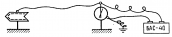 |
| Потенциальная энергия взаимодействия зарядов. | |
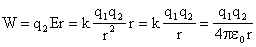 |  |
| Потенциал поля точечного заряда | |
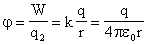 | |
| Потенциал заряженного шара а) Внутри шараЕ=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда. | 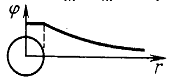 |
| Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными. |
Основные уравнения электростатики и их общее решение в бесконечном пространстве.
Уравнения электростатики получаются, если в общих уравнениях Максвелла частные производные по времени и плотность тока положить равными нулю:

Первое уравнение позволяет ввести потенциал
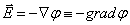
Тогда второе уравнение дает уравнение
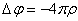
которое называется уравнением Пуассона.
Фундаментальное значение имеет уравнение для потенциала точечного заряда
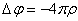
где 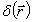 -дельта функция. Прямой проверкой показывается, что его решение есть
-дельта функция. Прямой проверкой показывается, что его решение есть
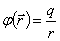
Это решение называется фундаментальным и позволяет написать общий вид решения уравнения Пуассона для произвольной плотности
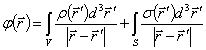
Первый интеграл описывает вклад объемного заряда с плотностью 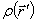 и называется ньютоновским потенциалом. Второй интеграл описывает вклад поверхностных зарядов с плотностью
и называется ньютоновским потенциалом. Второй интеграл описывает вклад поверхностных зарядов с плотностью 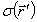 и называется поверхностным потенциалом.
и называется поверхностным потенциалом.
Используя связь потенциала и напряженности поля, получаем уравнение
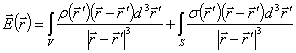
Две последние формулы дают решение прямой задачи электростатики в бесконечном пространстве (определение поля по распределению заряда).
13. Прямые задачи электростатики в ограниченном пространстве.
Если пространство ограничено, то для определения единственного решения уравнения Пуассона необходимо указать граничное условие. Различают две задачи.
Задача Дирихле (на границе задан потенциал)
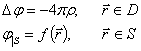
где 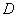 -область, в которой поставлена задача, а
-область, в которой поставлена задача, а 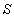 -ее граница.
-ее граница.
Задача Неймана (на границе задана нормальная производная потенциала)

Обе задачи имеют единственное решение.
14. Мультипольное разложение.
На расстояниях от системы точечных зарядов 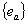 , много больших размеров системы, потенциал можно представить в виде сумму (разлагая в ряд Тейлора по малым
, много больших размеров системы, потенциал можно представить в виде сумму (разлагая в ряд Тейлора по малым 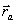 ):
):
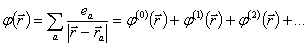
где
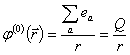 (
(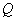 -полный заряд или мультиполь нулевого порядка),
-полный заряд или мультиполь нулевого порядка),
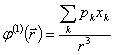 (
(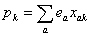 -дипольный момент или мультиполь первого порядка),
-дипольный момент или мультиполь первого порядка),
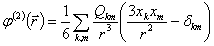 (
(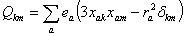 -квадрупольный момент или мультиполь второго порядка).
-квадрупольный момент или мультиполь второго порядка).
15. Некоторые методы решения задач электростатики.
Метод изображений.
Пусть сформулирована задача электростатики, в которой на некоторой поверхности задан постоянный потенциал. Тогда к реально существующим зарядам добавляются заряды изображения, величина которых и расположение подбираются так, чтобы в новой задачи указанная поверхность имела заданный потенциал. Примеры отражение в плоскости, отражение в сфере и так далее.
Метод инверсии.
К методу изображений близок метод инверсии, который основан на математической теореме об инверсии. Пусть 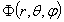 есть потенциал системы зарядов
есть потенциал системы зарядов 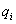 расположенных в точках со сферическими координатами
расположенных в точках со сферическими координатами 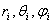 . Тогда
. Тогда
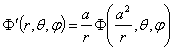
есть потенциал системы зарядов 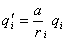 , расположенных в точках с координатами
, расположенных в точках с координатами 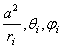 . Здесь
. Здесь 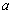 -некоторое действительное число.
-некоторое действительное число.
Теорема взаимности.
Пусть имеется система точечных зарядов 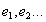 . Тогда потенциалы каждого заряда равны
. Тогда потенциалы каждого заряда равны
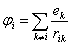
Пусть далее имеется другая система зарядов 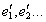 , в тех же точках. Тогда потенциалы равны
, в тех же точках. Тогда потенциалы равны
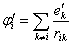
Умножим первое равенство на 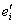 , второе на
, второе на 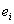 , оба просуммируем и вычтем одно из другого В результате получим
, оба просуммируем и вычтем одно из другого В результате получим
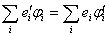
Нетрудно обобщить эту теорему и на неточечные проводники:
Если на проводниках 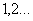 при зарядах
при зарядах 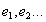 ,потенциалы равны
,потенциалы равны 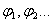 , а при зарядах
, а при зарядах 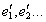 ,потенциалы равны
,потенциалы равны 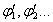 ,тогда выполняется соотношение
,тогда выполняется соотношение
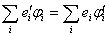
16. Уравнения Лапласа в декартовой, цилиндрической и полярной системах координат.
Уравнением Лапласа называется уравнение
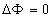
то есть это уравнение для потенциала при равной нулю плотности заряда.
Методом разделения переменных получается общий вид решения этого уравнения в различных системах координат.
В декартовой системе координат уравнение Лапласа имеет вид
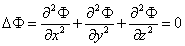
В цилиндрической системе координат уравнение Лапласа имеет вид
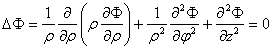
В сферической системе координат уравнение Лапласа имеет вид
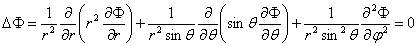
17. Уравнения теории для постоянных токов, граничные условия для токов.
В токостатике 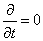 , но
, но 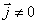 . Из уравнений Максвелла получаем
. Из уравнений Максвелла получаем
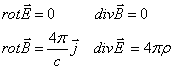
Отсюда следуют основные уравнения токостатики
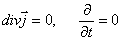
Для постоянной удельной проводимости эти уравнения эквиалентны
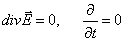
Граничные условия для токов имеют вид
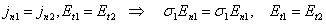
Задача токостатики в виде
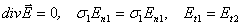
 2015-07-14
2015-07-14 14010
14010