Понятие линейного пространства | Примеры
Линейное, или векторное пространство 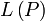 над полем P — это непустое множество L, на котором введены операции
над полем P — это непустое множество L, на котором введены операции
1. сложения, то есть каждой паре элементов множества 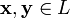 ставится в соответствие элемент того же множества, обозначаемый
ставится в соответствие элемент того же множества, обозначаемый 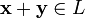 и
и
2. умножения на скаляр (то есть элемент поля P), то есть любому элементу 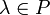 и любому элементу
и любому элементу 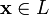 ставится в соответствие единственный элемент из
ставится в соответствие единственный элемент из 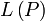 , обозначаемый
, обозначаемый 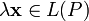 .
.
При этом на операции накладываются следующие условия:
1. 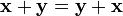 , для любых
, для любых 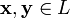 (коммутативность сложения);
(коммутативность сложения);
2. 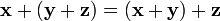 , для любых
, для любых 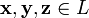 (ассоциативность сложения);
(ассоциативность сложения);
3. существует такой элемент 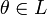 , что
, что 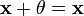 для любого
для любого 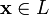 (существование нейтрального элемента относительно сложения), в частности L не пусто;
(существование нейтрального элемента относительно сложения), в частности L не пусто;
4. для любого 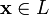 существует такой элемент
существует такой элемент 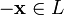 , что
, что 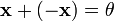 (существование противоположного элемента относительно сложения).
(существование противоположного элемента относительно сложения).
5. 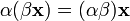 (ассоциативность умножения на скаляр);
(ассоциативность умножения на скаляр);
6. 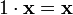 (унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).
(унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).
7. 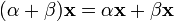 (дистрибутивность умножения на вектор относительно сложения скаляров);
(дистрибутивность умножения на вектор относительно сложения скаляров);
8. 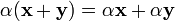 (дистрибутивность умножения на скаляр относительно сложения векторов).
(дистрибутивность умножения на скаляр относительно сложения векторов).
Элементы множества L называют векторами, а элементы поля P — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы.
БИЛЕТ №3
ОПРЕДЕЛЕНИЕ БАЗИСА ЛИНЕЙНОГО ПРОСТРАНСТВА
теорема о единственности разложения вектора по базису
Определение. Система векторов 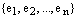 векторного пространства
векторного пространства 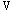 над полем К называется порождающей (образующей) системой векторов этого векторного пространства, если она представляет любой его вектор, т.е. если
над полем К называется порождающей (образующей) системой векторов этого векторного пространства, если она представляет любой его вектор, т.е. если 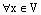 найдется такой набор скаляров
найдется такой набор скаляров 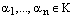 , что
, что 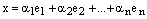 .
.
Определение. Система векторов векторного пространства называется минимальной порождающей системой, если при удалении из этой системы любого вектора она перестает быть порождающей системой.
Теорема. (О разложении вектора по базису.)
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
Доказательство. 1) Пусть L произвольная прямая (или ось) и 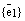 –базис
–базис 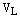 . Возьмем произвольный вектор
. Возьмем произвольный вектор 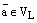 . Так как оба вектора
. Так как оба вектора 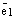 и
и 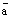 коллинеарные одной и той же прямой L, то
коллинеарные одной и той же прямой L, то 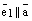 . Воспользуемся теоремой о коллинеарности двух векторов. Так как
. Воспользуемся теоремой о коллинеарности двух векторов. Так как 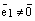 , то найдется (существует) такое число
, то найдется (существует) такое число 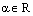 , что
, что 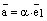 и тем самым мы получили разложение вектора
и тем самым мы получили разложение вектора 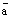 по базису
по базису 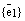 векторного пространства
векторного пространства 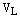 .
.
Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора 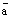 по базису
по базису 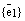 векторного пространства
векторного пространства 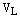 :
:
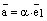 и
и 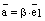 , где
, где 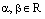 . Тогда
. Тогда 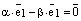 и используя закон дистрибутивности, получаем:
и используя закон дистрибутивности, получаем:
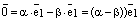 .
.
Так как 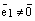 , то из последнего равенства следует, что
, то из последнего равенства следует, что 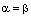 , ч.т.д.
, ч.т.д.
2) Пусть теперь Р произвольная плоскость и 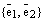 – базис
– базис 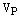 . Пусть
. Пусть 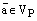 произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведемпрямую
произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведемпрямую 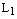 , на которой лежит вектор
, на которой лежит вектор 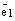 , прямую
, прямую 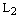 , на которой лежит вектор
, на которой лежит вектор 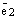 . Через конец вектора
. Через конец вектора 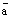 проведем прямую параллельную вектору
проведем прямую параллельную вектору 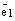 и прямую параллельную вектору
и прямую параллельную вектору 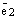 . Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма
. Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма 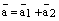 , и
, и 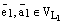 ,
, 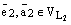 ,
, 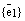 – базис
– базис 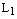 ,
, 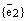 – базис
– базис 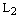 .
.
Теперь, по уже доказанному в первой части этого доказательства, существуют такие числа 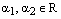 , что
, что
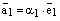 и
и 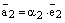 . Отсюда получаем:
. Отсюда получаем:
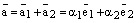 и возможность разложения по базису доказана.
и возможность разложения по базису доказана.
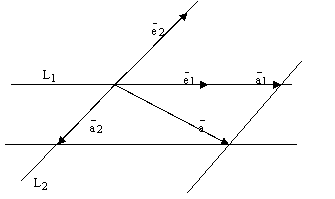
рис.3.
Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора 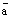 по базису
по базису 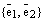 векторного пространства
векторного пространства 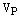 :
: 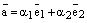 и
и 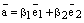 . Получаем равенство
. Получаем равенство
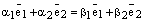 , откуда следует
, откуда следует 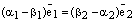 . Если
. Если 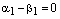 , то
, то 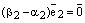 , а т.к.
, а т.к. 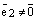 , то
, то 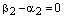 и коэффициенты разложения равны:
и коэффициенты разложения равны: 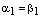 ,
, 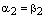 . Пусть теперь
. Пусть теперь 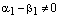 . Тогда
. Тогда 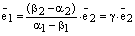 , где
, где 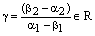 . По теореме о коллинеарностидвух векторов отсюда следует, что
. По теореме о коллинеарностидвух векторов отсюда следует, что 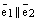 . Получили противоречие условию теоремы. Следовательно,
. Получили противоречие условию теоремы. Следовательно, 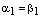 и
и 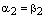 , ч.т.д.
, ч.т.д.
3) Пусть 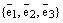 – базис
– базис 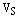 и пусть
и пусть 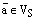 произвольный вектор. Проведем следующие построения.
произвольный вектор. Проведем следующие построения.
Отложим все три базисных вектора 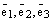 и вектор
и вектор 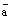 от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы
от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы 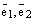 , плоскость
, плоскость 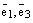 и плоскость
и плоскость 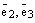 ; далее через конец вектора
; далее через конец вектора 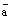 проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:
проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:
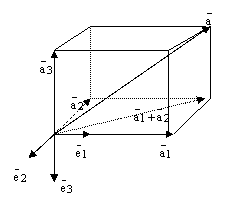
рис.4.
По правилу сложения векторов получаем равенство:
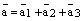 . (1)
. (1)
По построению 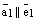 . Отсюда, по теореме о коллинеарности двухвекторов, следует, что существует число
. Отсюда, по теореме о коллинеарности двухвекторов, следует, что существует число 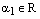 , такое что
, такое что 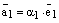 . Аналогично,
. Аналогично, 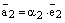 и
и 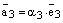 , где
, где 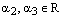 . Теперь, подставляя эти равенства в (1), получаем:
. Теперь, подставляя эти равенства в (1), получаем:
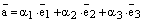 (2)
(2)
и возможность разложения по базису доказана.
Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора 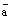 по базису
по базису 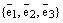 :
:
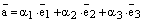 и
и 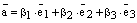 . Тогда
. Тогда
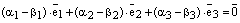 . (3)
. (3)
Заметим, что по условию векторы 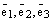 некомпланарные, следовательно, они попарно неколлинеарные.
некомпланарные, следовательно, они попарно неколлинеарные.
Возможны два случая: 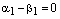 или
или 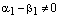 .
.
а) Пусть 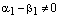 , тогда из равенства (3) следует:
, тогда из равенства (3) следует:
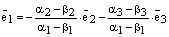 . (4)
. (4)
Из равенства (4) следует, что вектор 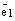 раскладывается по базису
раскладывается по базису 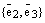 , т.е. вектор
, т.е. вектор 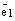 лежит в плоскости векторов
лежит в плоскости векторов 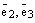 и, следовательно, векторы
и, следовательно, векторы 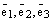 компланарные, что противоречит условию.
компланарные, что противоречит условию.
б) Остается случай 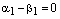 , т.е.
, т.е. 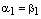 . Тогда из равенства (3) получаем
. Тогда из равенства (3) получаем 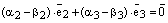 или
или
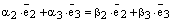 . (5)
. (5)
Так как 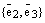 – базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что
– базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что 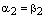 и
и 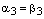 , ч.т.д.
, ч.т.д.
Теорема доказана.
 2015-08-13
2015-08-13 2132
2132
