Составление критериального уравнения

Порядок составления критериального уравнения рассмотрим на примере механической колебательной системы с одной степенью свободы, изображенной на рис.1.

Рис.1

Здесь приняты следующие обозначения:

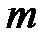- масса колеблющегося объекта, кг;

- жесткость упругого элемента, 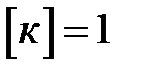Н/м;

- коэффициент сопротивления демпфера, 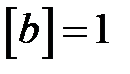Н с/м;

- перемещение объекта, 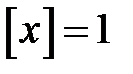м;

- внешнее воздействие в виде прямоугольного импульса, Н;

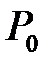- пиковое значение силового воздействия, 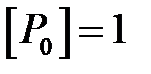Н;

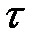- длительность импульса внешней силы, с;

- время, с.

Составим список параметров системы: . Будем полагать, что этот список, в рамках решаемой задачи, обладает свойством полноты. В качестве основныхпримем величины .Величины будут производными. Кратко список основных и производных величин представим в виде: . В первой круглой скобке – основные величины, а во второй – производные.

Возможен другой выбор основных величин. При этом необходимо, чтобы они имели независимые размерности в системе величин механики (см. приложение 3).

Размерности рассматриваемых величин:

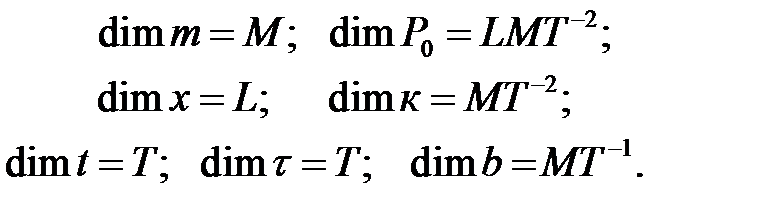
Количество безразмерных комплексов (критериев подобия) определяет - теорема: из общего числа размерных величин, характеризующих процесс, необходимо вычесть число основных величин, имеющих независимые размерности. В нашем случае число критериев подобия равно четырём.

Для определения критериев нужно каждую из величин 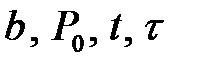,принятых в качестве производных, поочередно разделить на произведение основных величин, возведенных в некоторые степени :

(1.9)

(1.10)

(1.11)

(1.12)

Далее для каждого соотношения (1.9) – (1.12) составляется уравнение размерностей и определяются показатели степеней , которые затем подставляются в исходное выражение (1.9), (1.10), (1.11)или (1.12). Таким образом получаются безразмерные комплексы – критерии подобия.

1. Определение критерия подобия . Для формулы (1.9) составим уравнение размерностей. Так как с одной стороны

,

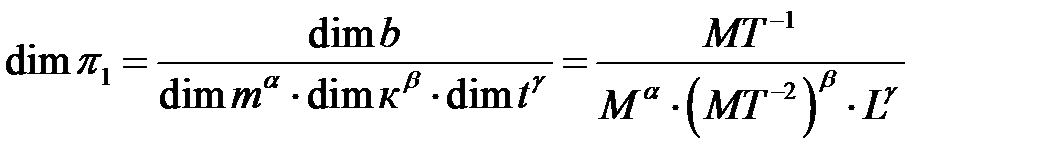а с другой

(величина безразмерная),

то можно записать уравнение размерностей:

.

Приравнивая показатели степеней при одинаковых величинах в левой и правой частях, получаем систему уравнений для их определения:

 

Отсюда: .Подставляя эти значения в формулу (1.9), находим:

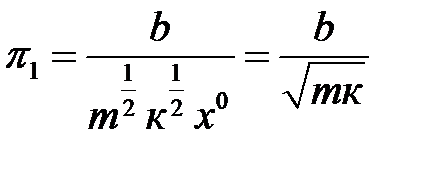. (1.13)

Величина имеет размерность коэффициента сопротивления .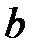

2. Определение критерия подобия 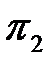. Уравнение размерностей, записанное для формулы (1.10), имеет вид:

.

Отсюда находим систему уравнений для определения показателей степеней

Решая эти уравнения, получаем: 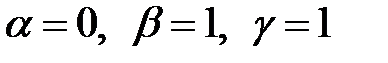. Подставляя найденные значения показателей степеней в соотношение (1.10), находим:

. (1.14)

Величина имеет размерность перемещения .

3. Определение критерия подобия 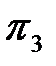. Для соотношения (1.11) запишем уравнение размерностей

.

Система уравнений для определения показателей степеней

Решение уравнений дает: . Подставляя полученные значения в (1.11), находим:

. (1.15)

Величина имеет размерность времени.

4. Критерий подобия 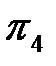находится по формуле (1.12) аналогично критерию :

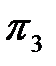. (1.16)

Критериальное уравнение выражает в общем виде зависимость между безразмерными комплексами :

или

.

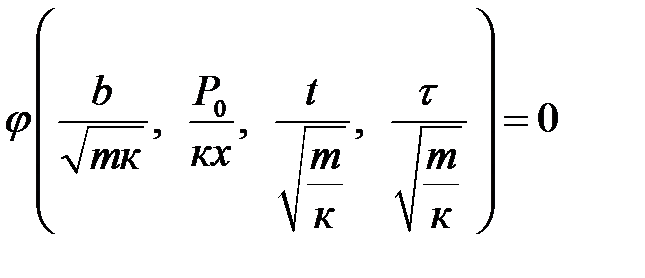Исходя из цели экспериментального исследования, критериальное уравнение можно представить в виде зависимости одного критерия подобия от других, например:

.

Следует заметить, что над критериями подобия можно выполнять операции умножения, деления, возведения в степень, извлечение корня, умножение на отвлеченное число, т.к. эти операции не изменяют безразмерности критериев. Это обстоятельство можно использовать, чтобы придать критериям более понятный физический смысл.

Обратимся к полученным критериям.

Критерий 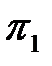(1.13) содержит величину . В теории колебаний используется понятие критического коэффициентасопротивления 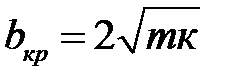.Критерий можно заменить на критерий . Его физический смысл – относительный коэффициент сопротивления демпфера.

Критерий (1.14) содержит величину , которую можно рассматривать как статическую деформацию упругого элемента под действием постоянной силы, равной пиковому значению . Обозначим эту величинучерез .Критерий заменим критерием . Физический смысл этого критерия – относительное перемещение объекта.

Критерий (1.15) содержит величину . Известна формула для определения периода собственных колебаний . Поэтому можно ввести критерий 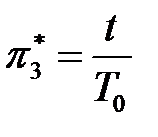, характеризующий относительное время.

Критерий (1.16) аналогичен критерию 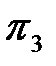(1,15).В силу этогопринимаем 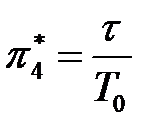. Он определяет относительную длительность импульса внешней силы.

Критериальное уравнение в новых критериях будет иметь вид:

.

Результаты эксперимента можно представить в виде графика зависимости относительного перемещения объекта от относительного времени при постоянных значениях относительного коэффициента сопротивления демпфера и относительной длительности импульса силы (рис.2).

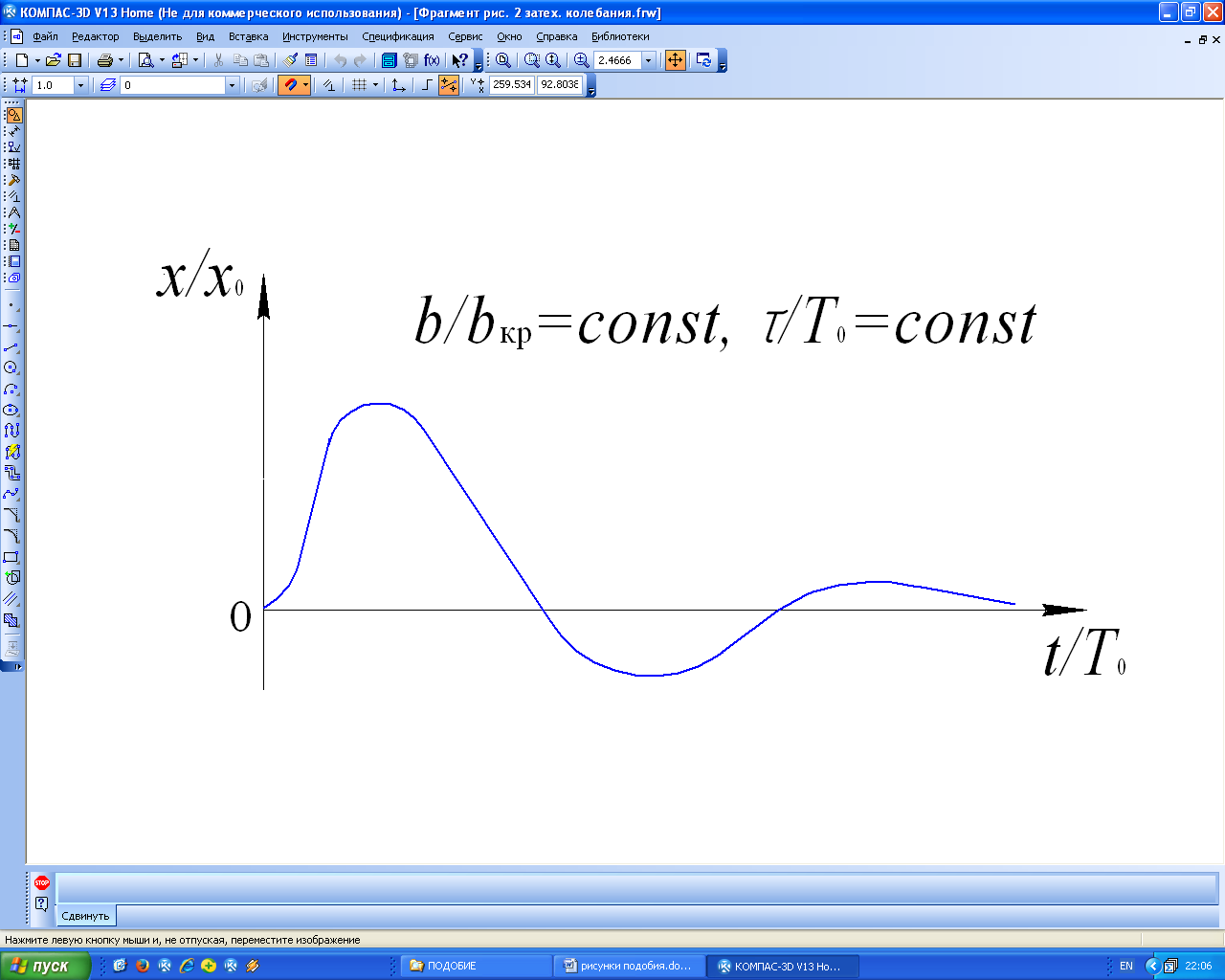
Рис.2

 

Такое представление результатов эксперимента позволяет обобщить их на весь класс подобных механических систем с одной степенью свободы, находящихся под действием прямоугольного импульса внешней силы при нулевых начальных условиях.