Определение теплоемкости воздуха

Под удельной теплоемкостью вещества понимают количество теплоты, которое нужно сообщить или отнять от единицы вещества (1 кг, 1 м³, 1 моль), чтобы изменить его температуру на один градус.

В зависимости от единицы заданного вещества различают следующие удельные теплоемкости:

- массовую теплоемкость С, отнесенную к 1 кг газа, Дж/(кг∙К);

- молярную теплоемкость µС, отнесенную к 1 кмолю газа, Дж/(кмоль∙К);

- объемную теплоемкость С′, отнесенную к 1 м³ газа, Дж/(м³∙К).

Удельные теплоемкости связаны между собой соотношением:

(1.1)

где υ_н - удельный объем газа при нормальных условиях (н.у.), м³/кг; µ - молярная масса газа, кг/кмоль.

Теплоемкость идеального газа зависит от характера процесса подвода (или отвода) теплоты, от атомности газа и температуры (теплоемкость реальных газов зависит также от давления).

Связь между массовыми изобарной С_P и изохорной С_V теплоемкостями устанавливается уравнением Майера:

С_P - С_V = R, (1.2)

где R – газовая постоянная, Дж/(кг∙К).

При нагревании идеального газа в замкнутом сосуде постоянного объема теплота расходуется только на изменение энергии движения его молекул, а при нагревании при постоянном давлении, благодаря расширению газа, одновременно совершается работа против внешних сил.

Для молярных теплоемкостей уравнение Майера имеет вид:

µС_р - µС_v = µR, (1.3)

где µR =8314Дж/(кмоль∙К) – универсальная газовая постоянная.

Объем идеального газа V_н, приведенный к нормальным условиям, определяется из следующего соотношения:

(1.4)

где Р_н – давление при нормальных условиях, Р_н = 101325 Па = 760 мм ртст; Т_н – температура при нормальных условиях, Т_н = 273,15 K; P_t, V_t, T_t – рабочие давление, объем и температура газа.

Отношение изобарной теплоемкости к изохорной обозначают k и называют показателем адиабаты:

(1.5)

Из (1.2) и с учетом (1.5) получаем:

(1.6)

Для точных расчетов средняя теплоемкость определяется по формуле:

(1.7)

В тепловых расчетах различного оборудования часто определяется количество тепла, которое требуется для нагрева или охлаждения газов:

Q = C∙m ∙(t ₂ - t ₁), (1.8)

Q = C′∙V_н ∙(t ₂ - t ₁), (1.9)

где V_н – объем газа при н.у., м³.

Q = µC∙ν ∙(t ₂ - t ₁), (1.10)

где ν – количество газа, кмоль.

Теплоемкость. Использование теплоемкости для описания процессов в закрытых системах

В соответствии с уравнением (4.56) теплота может быть определена, если известно изменение энтропии S системы. Однако то обстоятельство, что энтропия не может быть измерена непосредственно, создает некоторые осложнения, особенно при описании изохорных и изобарных процессов. Возникает необходимость в определении количества теплоты с помощью измеряемой на опыте величины.

В качестве такой величины может выступать теплоемкость системы. Наиболее общее определение теплоемкости вытекает из выражения первого закона термодинамики (5.2), (5.3). Исходя из него, любая емкость системы С по отношению к работе вида m определяется уравнением

C_m = dA_m / dP_m = P_md_eg_m / dP_m, (5.42)

где С_m – емкость системы;

P_m и g_m – соответственно обобщенный потенциал и координата состояния вида m.

Величина C_m показывает, какое количество работы вида m необходимо совершить при заданных условиях, чтобы изменить m-й обобщенный потенциал системы на единицу его измерения.

Понятие емкости системы по отношению к той или иной работе в термодинамике широко используется лишь при описании теплового взаимодействия между системой и окружающей средой.

Емкость системы по отношению к теплоте называется теплоемкостью и задается равенством

С = d_eQ / dT = Td_eS_тепл / dT. (5.43)

Таким образом, теплоемкость может быть определена как количество теплоты, которое необходимо сообщить системе, чтобы изменить ее температуру на один Кельвин.

Теплоемкость, подобно внутренней энергии и энтальпии, является экстенсивной величиной, пропорциональной количеству вещества. На практике используют теплоемкость, отнесенную к единице массы вещества, – удельную теплоемкость, и теплоемкость, отнесенную к одному молю вещества, – молярную теплоемкость. Удельная теплоемкость в СИ выражается в Дж/(кг·К), а молярная – в Дж/(моль·К).

Удельная и молярная теплоемкости связаны соотношением:

С_моль = С_удМ, (5.44)

где М - молекулярная масса вещества.

Различают истинную (дифференциальную) теплоемкость, определяемую из уравнения (5.43) и представляющую собой элементарное приращение теплоты при бесконечно малом изменении температуры, и среднюю теплоемкость, представляющую собой отношение полного количества теплоты к полному изменению температуры в данном процессе:

= Q/DT. (5.45)

Связь между истинной и средней удельной теплоемкостью устанавливается соотношением

= / DT (5.46)

или

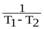
= . (5.47)

При постоянных давлении или объеме теплота и соответственно теплоемкость приобретают свойства функции состояния, т.е. становятся характеристиками системы. Именно эти теплоемкости - изобарную С_Р (при постоянном давлении) и изохорную С_V (при постоянном объеме) наиболее широко используют в термодинамике.

Если система нагревается при постоянном объеме, то в соответствии с выражением (5.27) изохорная теплоемкость C_V записывается в виде

C_V = . (5.48)

Если система нагревается при постоянном давлении, то в соответствии с уравнением (5.32) изобарная теплоемкость С_Р предстает в виде

С_Р = . (5.49)

Чтобы найти связь между С_Р и С_V, надо продифференцировать выражение (5.31) по температуре. Для одного моля идеального газа это выражение с учетом уравнения (5.18) можно представить в виде

H = U + pV = U + RT. (5.50)

Тогда

dH/dT = dU/dT + R, (5.51)

а разность между изобарной и изохорной теплоемкостями для одного моля идеального газа численно равна универсальной газовой постоянной R:

С_Р - С_V = R. (5.52)

Теплоемкость при постоянном давлении всегда больше теплоемкости при постоянном объеме, так как нагревание вещества при постоянном давлении сопровождается работой расширения газа.

Используя выражение внутренней энергии идеального одноатомного газа (5.21), получим значение его теплоемкости для одного моля идеального одноатомного газа:

C_V = dU/dT = d(3/2 RT)dT = 3/2 R» 12,5 Дж/(моль·К); (5.53)

C_Р = 3/2R + R = 5/2 R» 20,8 Дж/(моль·К). (5.54)

Таким образом, для одноатомных идеальных газов C_VиC_p не зависит от температуры, поскольку вся подведенная тепловая энергия расходуется только на ускорение поступательного движения. Для многоатомных молекул наряду с изменением поступательного движения может происходить и изменение вращательного и колебательного внутримолекулярного движения. Для двухатомных молекул обычно учитывают дополнительно вращательное движение, вследствие чего численные значения их теплоемкостей составляют:

C_V = 5/2 R» 20,8 Дж/(моль·К); (5.55)

C_p = 5/2 R + R = 7/2 R» 29,1 Дж/(моль·К). (5.56)

Попутно коснемся теплоемкостей веществ в других (кроме газообразного) агрегатных состояниях. Для оценки теплоемкостей твердых химических соединений нередко используют приближенное правило аддитивности Неймана и Коппа, согласно которому молярная теплоемкость химических соединений в твердом состоянии равна сумме атомных теплоемкостей элементов, входящих в данное соединение. Так, теплоемкость сложного химического соединения с учетом правила Дюлонга и Пти можно оценить так:

C_V = 25n Дж/(моль·К), (5.57)

где n - число атомов в молекулах соединений.

Теплоемкости жидкостей и твердых тел вблизи температуры плавления (кристаллизации) почти равны. Вблизи нормальной температуры кипения большинство органических жидкостей имеет удельную теплоемкость 1700 - 2100 Дж/кг·К. В промежутках между этими температурами фазовых переходов теплоемкость жидкости может значительно отличаться (зависит от температуры). В общем виде зависимость теплоемкости твердых тел от температуры в интервале 0 – 290К в большинстве случаев хорошо передается полуэмпирическим уравнением Дебая (для кристаллической решетки) в области низких температур

C_Р» C_V = eT³, (5.58)

в котором коэффициент пропорциональности (e) зависит от природы вещества (эмпирическая константа).

Зависимость теплоемкости газов, жидкостей и твердых тел от температуры при обычных и высоких температурах принято выражать с помощью эмпирических уравнений, имеющих вид степенных рядов:

С_Р = a + bT + cT² (5.59)

или

С_Р = a + bT + c'T^-2, (5.60)

где a, b, c и c' - эмпирические температурные коэффициенты.

Возвращаясь к описанию процессов в закрытых системах с привлечением метода теплоемкостей, запишем некоторые уравнения, приведенные в параграфе 5.1, в несколько ином виде.

Изохорный процесс. Выражая внутреннюю энергию (5.27) через теплоемкость, получим

dU_V = dQ_V = U₂ – U₁ = C_V dT = 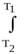C_V dT. (5.61)

С учетом того, что теплоемкость идеального газа не зависит от температуры, уравнение (5.61) можно записать так:

DU_V = Q_V = U₂ - U₁ = C_VDT. (5.62)

Чтобы вычислить значение интеграла (5.61) для реальных одно- и многоатомных газов, надо знать конкретный вид функциональной зависимости C_V = f(T) типа (5.59) или (5.60).

Изобарный процесс. Для газообразного состояния вещества первый закон термодинамики (5.29) для этого процесса с учетом записи работы расширения (5.35) и с использованием метода теплоемкостей записывается так:

Q_Р = С_VDT + RDT = C_РDT = DH (5.63)

или

Q_Р = DH_Р = H₂ – H₁ = 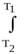C_РdT. (5.64)

Если система является идеальным газом и теплоемкость С_Р не зависит от температуры, соотношение (5.64) переходит в (5.63). Для решения уравнения (5.64), описывающего реальный газ, необходимо знать конкретный вид зависимости C_p = f(T).

Изотермический процесс. Изменение внутренней энергии идеального газа в процессе, протекающем при постоянной температуре

dU_T= C_VdT = 0. (5.65)

Адиабатический процесс. Так как dU = C_VdT, то для одного моля идеального газа изменение внутренней энергии и совершаемая работа равны соответственно:

DU = C_VdT = C_V(T₂ - T₁); (5.66)

А_мех = -DU = C_V(T₁ - T₂). (5.67)

Анализ уравнений, характеризующих различные термодинамические процессы при условиях: 1) p = сonst; 2) V = сonst; 3) T = сonst и 4) dQ = 0 показывает, что все они могут быть представлены общим уравнением:

pVⁿ = сonst. (5.68)

В этом уравнении показатель "n" может принимать значения от 0 до¥ для разных процессов:

1. изобарного (n = 0);

2. изотермического (n = 1);

3. изохорного (n = ¥);

4. адиабатического (n = g; где g = C_Р/C_V – адиабатический коэффициент).

Полученные соотношения справедливы для идеального газа и представляют собой следствие его уравнения состояния, а рассмотренные процессы - частные и предельные проявления реальных процессов. Реальные же процессы, как правило, являются промежуточными, протекают при произвольных значениях "n" и получили название политропных процессов.

Если сравнить работу расширения идеального газа, производимую в рассмотренных термодинамических процессах, с изменением объема от V₁ до V₂, то, как видно из рис. 5.2, наибольшая работа расширения совершается в изобарном процессе, меньшая – в изотермическом и еще меньшая – в адиабатическом. Для изохорного процесса работа равна нулю.

Рис. 5.2. P = f (V) –зависимость для различных термодинамических процессов (заштрихованные области характеризуют работу расширения в соответствующем процессе)