Вероятность суммы совместных событий

Теорема. Вероятность суммы двух совместных событи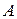й и 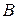равна сумме вероятностей этих событий без учета вероятности произведения этих событий: .

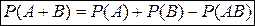Если события 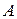и 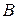несовместны, то 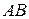- невозможное событие. Тогда 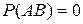, и мы получаем формулу .

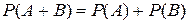Пример 8. Определим вероятность выпадения хотя бы одной единицы при двух бросаниях кубика.

Событие 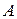 - при 1-м бросании выпало число 1, событие 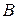- при 2-м бросании выпало число 1. тогда событие  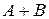- «хотя бы один раз выпало число 1».

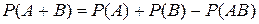= 1/6 + 1/6 – 1/36 =11/36.

Пример 9. Вероятности своевременного выполнения задания двумя работниками фирмы соответственно равны 0,8 и 0,7. Работники получили независимо друг от друга задание.

Найти вероятности событий:

1) только один работник выполнит задание в срок;

2) хотя бы один работник выполнил задание в срок.

Решение

Введем события: 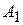 - первый работник выполнил задание в срок,  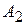- второй работник выполнил задание в срок.

По условию, их вероятности ; .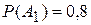

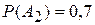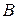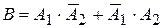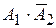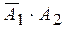1) Событие – «Только один работник выполнил задание в срок», тогда . Слагаемые и несовместны, поэтому по теореме сложения вероятностей двух несовместных событий имеем

.

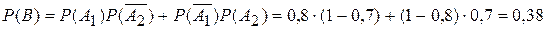2) Существует несколько способов нахождения вероятности события 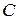– «Выполнил задание в срок хотя бы один работник».

Первый способ связан с применением теоремы сложения вероятностей совместных событий. Так как события 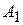и 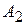совместны, то .

Во втором способе дается полное представление о структуре события 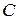. Событие 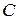представим в виде суммы событий: .

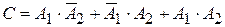Сумма первых двух слагаемых 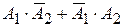соответствует событию 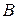«Только один работник выполнил задание в срок», слагаемое 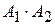– событию «Оба работника выполнили задание в срок». Тогда вероятность события 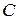– «Хотя бы один работник выполнил задание в срок» равна

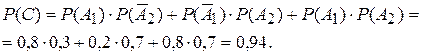
Третий способ заключается в использовании противоположного события. Рассмотрим противоположные события: 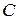– «Хотя бы один работник выполнил задание в срок» и 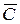- «Оба работника не выполнили задание в срок», или 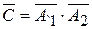. Сумма вероятностей противоположных событий равна единице 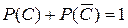, отсюда

.

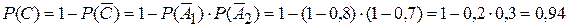Как видно, все три способа вычисления вероятности события 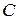дали один и тот же результат.