Системы автоматического управления промышленными роботами

Главная особенность САУ промышленными роботами - это их

автономная работа без непосредственного участия человека. Функции оператора состоят лишь в обучении, запуске и последующем периоди­ческом наблюдении за работой робота.

САУ промышленными роботами делятся на следующие классы.

1. Системы программного управления, основой которых явля­ется синтез движения робота по заранее рассчитанной преимуществен­но жесткой программе. Программа сохраняется в памяти вычислитель­ного устройства и может быть изменена путем перепрограммирования в новом цикле обучения робота. В системах программного управления не предусматривается отработка информации, устраняющая неопреде­ленность характеристик внешней среды, хотя информация о внутрен­нем фазовом состоянии робота используется в законе управления.

2. Системы адаптивного управления - это системы управления, движение робота в которьгх организуется по гибко изменяемым или корректируемым программам. При этом перестройка программ проис­ходит в ответ на изменение условий внешней среды. Для получения внешней информации адаптивные системы управления обеспечиваются разнообразными средствами очувствления.

3. Системы интеллектного управления - это системы управления, в которых программа движения робота вообще не задается, а синтези­руется на основе описания внешней среды, совокупности правил воз­можного поведения в среде и имеющейся целевой установки задачи. Основное отличие интеллектных систем управления - способность из­влекать из данных не только информацию, а еще и знания. Для этой це­ли системы очувствления дополняются системами понимания (пред­ставления знаний).

Закон управления в САУ реализуется в виде программы управле­ния. При этом возможны различные режимы отработки заданной про­граммы. Управление по жесткой программе без ее перестройки в процессе работы. Жесткая отработка программы характерна для робо­тов перого поколения. Это наиболее простой вид управления, особенно при реализации его на базе разомкнутого цикла управления. В более сложных случаях применяют замкнутый принцип управления. Адап­тивное изменение программы в зависимости от условий работы. Наличие системы очувствления позволяет роботу приспосабливаться к не полностью определенной обстановке при выполнении программы, отличает автоматические роботы второго поколения, называемые адап­тивными. Формирование управления при отсутствии заданной в явном виде программы. Способность восприятия, распознавания ок­ружающей среды, построение ее модели, принятие решения об измене­нии поведения при выполнении задания характерны для роботов третьего поколения. Эти роботы называются интеллектными, т.к. они технически воспроизводят отдельные, достаточно сложные интеллекту­альные функции, свойственные человеку.

Динамика роботов

 

При описании динамических свойств робота обычно анализируют отдельно манипулятор, рассматриваемый в качестве механической сис­темы, представляющей собой совокупность звеньев с определенными массоинерционными характеристиками, и приводы робота.

Для получения уравнений динамики используются различные подходы. Рассмотрим динамическую модель манипулятора [4], полу­ченную на основе уравнений Лагранжа П-го рода:

где к = 1, 2,..., N; L = К-П - функция Лагранжа; К - кинетическая энергия системы; П - потенциальная энергия системы; F_k - обобщенная сила, отнесенная к k-му звену; q_k - обобщенная координата k-го звена. Опуская сложные выкладки, запишем уравнение динамики работы ма­нипулятора в виде

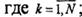
где F_i - матрица преобразования i-го звена, описывающая его положе­ние в системе координат О₀, x₀, у₀, z₀; t_r - след матрицы, равный сумме ее диагональных элементов; H_i - матрица инерции i-ro звена; N - чис­ло подвижных звеньев; m_i - масса i-ro звена; G^T - вектор ускорения свободного падения, т.е.

R_ц - радиус-вектор центра масс i-ro звена в соответствующей ему сис­теме координат.

Приведенное уравнение показывает сложность управления мани­пулятором. Однако системы управления роботом разрабатываются не с учетом указанной модели манипулятора, а, в первую очередь, на основе уравнений динамики приводов, которые формируют управляющие воз­действия на вход манипулятора с учетом данной модели, получаемой специалистами соответствующего профиля.

Вид уравнений динамического привода, связывающих управляю­щие воздействия с развиваемыми моментами (усилиями), определяется с учетом нелинейностей привода. В качестве примера рассмотрена ли­неаризованная модель привода, механическая часть которого считается абсолютно жесткой.

Динамика линеаризованного привода описывается следующей системой уравнений:

-уравнение усилителя привода

где к = l,N; к_yk - коэффициент пропорциональности; А_yk(р) - оператор­ный многочлен, характеризующий инерционность усилителя; ω_ДXk - угловая (или линейная) скорость, зависящая от управляющего воздей­ствия v_k(t);

-уравнение двигателя привода

где k = l,N; к_Дk - коэффициент пропорциональности; В_Дк(р) - оператор­ный многочлен, характеризующий инерционность двигателя; M_Дk(t) -развиваемый двигателем момент (усилие);   - угловые (или линейные) скорости перемещений объекта управления и двигателя по координате q_x

- уравнение моментов (усилий) на валу двигателя

 

где J_Дk - момент инерции (или масса) перемещающихся частей двигате­ля; M_Дk(t) - создаваемый нагрузкой суммарный момент (усилие); M_НДk(t) - приведенный к валу двигателя момент (усилие) нагрузки M_Нk(t);

-уравнение приведенной скорости вала двигателя привода

где i_pk - передаточное число редуктора (i_pk > 1);

-уравнение приведенного момента (усилия) нагрузки

где

где h_k - коэффициент полезного действия редуктора.

Приведенные уравнения справедливы для приводов не только с угловым, но и с линейным перемещением (при замене моментов сил на усилия, а моментов инерции на массы).

Структурная схема линеаризованного привода, соответствующая данной системе уравнений, приведена на рис. 2.7.

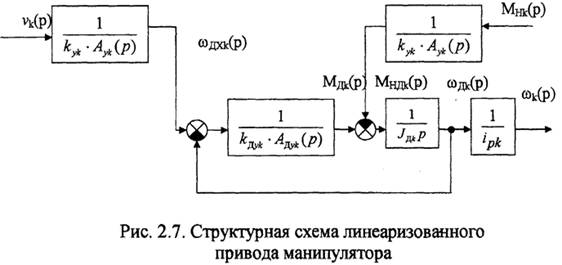
Дифференциальные уравнения привода в операторной форме, свя­зывающие управляющее воздействие v_k(t) со скоростью вала нагрузки ω_k(t) и с приведенным к валу нагрузки моментом M_Нk(t), развиваемым двигателем, имеют вид:

 

 

Полученные передаточные функции (2.38) и (2.39) используют при моделировании систем управления приводов промышленных робо­тов.