2018-02-14
1304
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
"САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА
(национальный исследовательский университет)"
КОЛЕБАНИЯ И ВОЛНЫ
Задачи для аудиторной и самостоятельной работы
Самара 2012
УДК 53(075)
Составители: Г.Ю. Баландина, Е.А.Китаева, В.Г. Макарян, И.Л. Стукалина
Колебания и волны: Задачи для аудиторной и самостоятельной работы / Самарский гос. аэрокосм. ун-т. Сост. Г.Ю. Баландина, Е.А.Китаева, В.Г. Макарян, И.Л. Стукалина; Самара, 2011. 20 с.
Пособие содержит вопросы для самоконтроля, принятые обозначения и основные формулы. Методические указания составлены в соответствии с программой по физике для студентов дневного отделения радиотехнического факультета. Подготовлено на кафедре физики.
Печатается по решению редакционно-издательского совета Самарского государственного аэрокосмического университета имени академика С.П. Королёва.
Рецензент: д.т.н., профессор В.И.Богданович.
Вопросы:
3 Законы изменения координат, скоростей, ускорений и энергии при гармоническом колебательном движении.
4 Сложение колебаний одного направления и одинаковой частоты.
5 Сложение взаимно перпендикулярных колебаний.
7 Характеристики затухающих колебаний.
Принятые обозначения:
· 
− смещение от положения равновесия.
· 
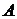− амплитуда колебаний.
· 
− угловая частота.
· 
− фаза колебаний.
· 
− частота колебаний.
· 
− скорость колеблющейся точки.
· 
− ускорение колеблющейся точки.
· 
− период колебания.
· 
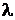− логарифмический декремент затухания.
· 
− добротность системы.
Основные формулы:
· Уравнение гармонических колебаний:
.
· Скорость при гармоническом колебании:
.
· Ускорение при гармоническом колебании:
.
· Угловая частота колебаний:
и 
.
· Амплитуда результирующего колебания, полученного при сложении двух колебаний одного направления с одинаковыми частотами:
,
где 
и 
− амплитуды складываемых колебаний, 
и 
− начальные фазы.
· Начальная фаза результирующего колебания:
.
· Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях:
.
· Полная энергия материальной точки при гармонических колебаниях:
.
· Период колебаний пружинного маятника:
,
где 
− жесткость пружины.
· Период колебаний математического маятника:
,
где 
− длина маятника.
· Период колебаний физического маятника:
,
где 
− момент инерции тела, − расстояние от оси колебания до центра масс маятника.
· Частота малых колебаний материальной точки массы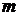 
около положения равновесия 
в потенциальном поле 
:
,
где 
− коэффициент квазиупругой силы.
· Уравнение затухающих колебаний:
.
· Угловая частота затухающих колебаний:
.
· Логарифмический декремент затухания:
.
· Добротность контура:
.
Задачи
1 Начальная фаза синусоидального гармонического колебания равна нулю. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?
2 Уравнение колебаний материальной точки массой 10 г имеет вид 
см. найти максимальную силу, действующую на точку, и полную энергию колеблющейся точки.
3 Как изменится период вертикальных колебаний груза, висящего на двух одинаковых пружинах, если от последовательного соединения пружин перейти к параллельному их соединению?
4 В результате сложения двух одинаково направленных гармонических колебаний с одинаковыми амплитудами и одинаковыми периодами получается результирующее колебание с тем же периодом и той же амплитудой. Найти разность фаз складываемых колебаний.
5 Чему равен логарифмический декремент затухания математического маятника, если за 1 минуту амплитуда колебаний уменьшилась в два раза? Длина маятника 1 м.
6 Математический маятник совершает затухающие колебания с логарифмическим декрементом затухания 0,2. Во сколько раз уменьшится полное ускорение маятника в его крайнем положении за одно колебание?
7 Частица совершает гармонические косинусоидальные колебания вдоль оси около положения равновесия 
. Частота колебаний =4 рад/с. В некоторый момент координата частицы 
=25 см, а ее скорость 
=100 см/с. Найти координату и скорость частицы через 2,4 с после этого момента.
8 Представим себе шахту, пронизывающую Землю по ее оси вращения. Считая Землю за однородный шар (
м) и пренебрегая сопротивлением воздуха, найти: уравнение движения тела, упавшего в шахту; время, которое понадобится этому телу, чтобы достигнуть противоположного конца шахты; скорость тела в центре Земли.
9 Доска с лежащим на ней бруском совершает горизонтальные гармонические колебания с амплитудой 10 см. Найти коэффициент трения между доской и бруском, если последний начинает скользить по доске, когда ее период колебаний меньше 1 с.
10 Найти период малых вертикальных колебаний тела массы 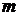, подвешенного на двух последовательно соединенных пружинах, жесткости которых равны 
и 
, а их массы пренебрежимо малы.
11 Тело 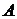массы 
=1 кг и тело 
массы 
=4,1 кг соединены между собой пружиной, как показано на рисунке 1. Тело 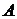совершает свободные вертикальные гармонические колебания с амплитудой 1,6 см и частотой =25 рад/с. Пренебрегая массой пружины, найти наибольшее и наименьшее значение силы давления этой системы на опорную плоскость.
12 
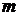Частица массы находится в одномерном потенциальном поле, где потенциальная энергия зависит от координаты как 
, 
и − некоторые постоянные. Найти период малых колебаний частицы около положения равновесия.
13 Частица массы 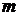находится в одномерном потенциальном поле, где потенциальная энергия зависит от координаты как 
, и 
− некоторые положительные постоянные. Найти период малых колебаний частицы около положения равновесия.
14 
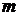Частица массы находится в одномерном потенциальном поле, где потенциальная энергия зависит от координаты как 
, и − некоторые постоянные. Найти период малых колебаний частицы около положения равновесия.
15 
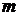Шарик с массой и зарядом 
находится внутри непроводящей трубки между двумя неподвижными заряженными шариками (рисунок 2). Найти период малых колебаний шарика около положения равновесия, если заряды неподвижных шариков равны , а расстояние между их центрами .
16 
Вычислить период малых колебаний ареометра (рисунок 3), которому сообщили небольшой толчок в вертикальном направлении. Масса ареометра 
, радиус его трубки 
, плотность жидкости 
. Сопротивление жидкости считать пренебрежимо малым.
17 Найти частоту малых колебаний системы, показанной на рисунке 4. Известны радиус блока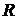 
, его момент инерции относительно оси вращения 
, масса тела 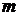и жесткость пружины . Массы нити и пружины пренебрежимо малы, нить по блоку не скользит, трения в оси блока нет.
18 Найти период малых вертикальных колебаний шарика массы 
, укрепленного на середине горизонтально натянутой струны длины 
. Натяжение струны считать постоянным и равным 
.
19 Однородный диск радиуса 
может вращаться вокруг горизонтальной оси, перпендикулярной к его плоскости и проходящей через край диска. Найти период малых колебаний этого диска, если логарифмический декремент затухания 
.
20 Шарик массы 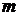, подвешенный на пружине, удлиняет ее на величину 
. Под действием внешней вертикальной силы, меняющейся по гармоническому закону с амплитудой 
, шарик совершает вынужденные колебания. Логарифмический декремент затухания равен 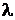. Пренебрегая массой пружинки, найти круговую частоту вынуждающей силы, при которой амплитуда смещения шарика максимальна. Каково значение этой амплитуды?
21 Некоторая точка совершает затухающие колебания с частотой 
. Найти коэффициент затухания 
, если в начальный момент скорость точки равна нулю, а ее смещение из положения равновесия в 
раза меньше амплитуды в этот момент.
22 Найти добротность математического маятника длины 
, если за промежуток времени 
его полная механическая энергия уменьшилась в 
раз.
23 Найти добротность осциллятора, у которого амплитуда смещения уменьшается в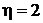 
раза через каждые 
колебаний.
24 Частицу сместили из положения равновесия на расстояние 
и предоставили самой себе. Какой путь пройдет, колеблясь, эта частица до полной остановки, если логарифмический декремент затухания 
?
Ответы
1. T/6. 2. 
Н; 
Дж. 3. Уменьшится в 2 раза. 4. 
. 5. 0,023. 6. 1,22. 7. –29 см; -81 см/с. 8. 42 мин; 7,2 км/час. 9. 
0,4. 10. 
. 11. 60 Н; 40 Н. 12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
, 
21. 
. 22. 
23. 
24. 
.
