Непрерывная случайная величина Х имеет нормальный закон распределения, с параметрами a (математическое ожидание) и s (среднее квадратическое отклонение), если ее плотность вероятности имеет вид:
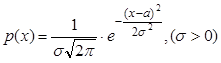 (6)
(6)
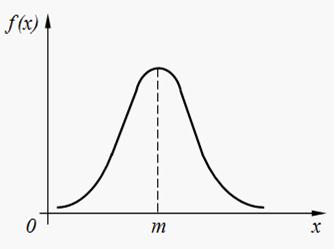
Рис.2. График плотности нормального распределения
График функции (6) называют нормальной кривой (рис.2.)
Функция распределения нормально распределенной случайной величины имеет вид:
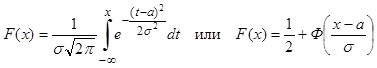 (7)
(7)
Нормальное распределение с параметрами 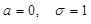 называется нормированным или стандартным, при этом плотность распределения принимает вид:
называется нормированным или стандартным, при этом плотность распределения принимает вид:
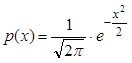 (8)
(8)
Вероятность попадания нормально распределенной случайной величины Х в интервал 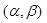 определяется формулой:
определяется формулой:
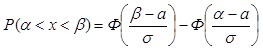 (9)
(9)
где 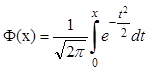 - функция Лапласа
- функция Лапласа
С помощью функции Лапласа определяют вероятность отклонения нормальной случайной величины от среднего значения используя неравенство 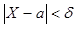 , здесь а математическое ожидание (среднее значение) нормально распределенной величины Х:
, здесь а математическое ожидание (среднее значение) нормально распределенной величины Х:
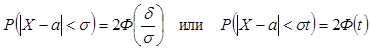 (10)
(10)
где 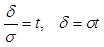
Нормальное распределение является наиболее часто встречающимся в различных случайных явлениях природы.
Например, нормальное или близко к нормальному имеют распределение, следующие величины:
ü вес пойманной рыбы;
ü стоимость акций на рынке;
ü ошибки параметров компьютерных систем;
ü вес и размеры выращенных овощей;
ü цена на определенный товар или изделие;
ü случайные величины, образованные суммированием большого количества случайных слагаемых.
Пример 5: Случайная величина Х имеет нормальное распределение и известны числовые характеристики 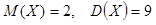 . Записать плотность распределения и функцию распределения вероятностей случайной величины Х.
. Записать плотность распределения и функцию распределения вероятностей случайной величины Х.
Решение: Поскольку случайная величина Х - нормально распределена и по условию задачи параметры распределения величины Х:
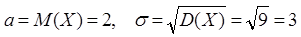
Подставим эти значения в формулу (6), получим
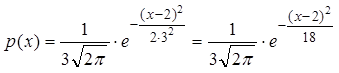 0
0
Теперь по формуле (7) найдем функцию распределения вероятностей
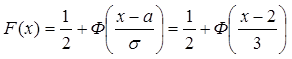
Ответ: 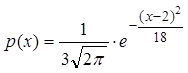 и
и 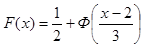
Пример 6: Случайная величина Х имеет нормальное распределение и известны числовые характеристики 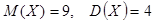 . Найти 1)
. Найти 1) 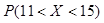 , 2)
, 2) 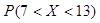 .
.
Решение: Так как случайная величина Х - нормально распределена и по условию задачи параметры распределения величины Х:
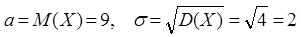
Подставим эти значения в формулу (9), получим
1) 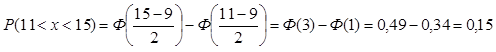
2) 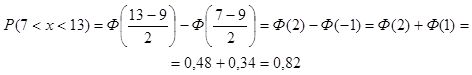
Ответ: 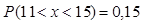 и
и 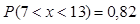
Пример 7: Вес пойманной рыбы подчиняется нормальному закону распределения с параметрами 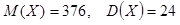 . Найти 1)
. Найти 1) 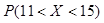 , 2)
, 2) 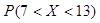 .
.
Решение: Так как случайная величина Х - нормально распределена и по условию задачи параметры распределения величины Х:
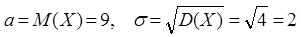
Подставим эти значения в формулу (9), получим
3) 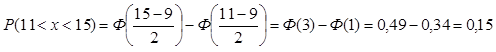
4) 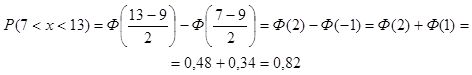
Ответ: 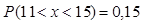 и
и 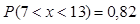
 2014-02-12
2014-02-12 8865
8865