Рассмотрим реализацию серии п независимых испытаний в каждом из которых данное событие А имеет одну и ту же вероятность 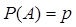 , не зависящую от номера испытания. И для каждого испытания имеются только два исхода:
, не зависящую от номера испытания. И для каждого испытания имеются только два исхода:
3) событие А – успех;
4) событие 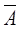 - неуспех,
- неуспех,
с постоянными вероятностями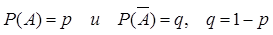
Если число независимых испытаний n устремить к ∞, а вероятность p устремить к нулю так, чтобы np стремилось к некоторой постоянной а, то биномиальное распределение будет неограниченно приближаться к распределению Пуассона. В общем случае говорят, что случайная величина X распределена по закону Пуассона, если она может принимать только целые неотрицательные значения, а вероятности этих значений определяются формулой Пуассона:
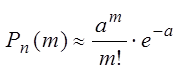 (9)
(9)
где 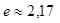 , экспонента и
, экспонента и 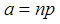 .
.
Закон распределения Пуассона дискретной случайной величины представляют в виде таблицы:
| Х | 0 | 1 | 2 | … | k | … |
| Р | 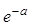 | 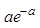 | 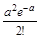 | … | 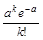 | … |
при этом 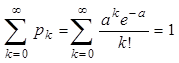
Основные числовые характеристики распределения Пуассона:
1) математическое ожидание 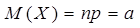 (10)
(10)
2) дисперсия 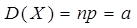 (11)
(11)
3) среднее квадратическое отклонение 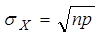 (12)
(12)
Распределение Пуассона используется при анализе результатов выборочных маркетинговых обследований потребителей, расчете характеристик статистического приемочного контроля в случае малых значений приемочного уровня дефектности, для описания числа разладок статистически управляемого технологического процесса в единицу времени, числа «требований на обслуживание», поступающих в единицу времени в систему массового обслуживания, статистических закономерностей несчастных случаев и редких заболеваний, и т.д.
Пример 3: Случайная величина Х распределена по закону Пуассона. Найти математическое ожидание, дисперсию и 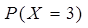 , если а=4.
, если а=4.
Решение: По формуле (9) при известных 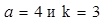 получим
получим
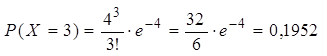
Теперь найдем числовые характеристики Х:
ü дисперсия 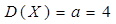
ü среднее квадратическое отклонение 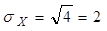
Ответ: 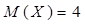
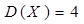
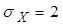
Пример 4: Случайная величина Х распределена по закону Пуассона. Найти математическое ожидание, дисперсию и 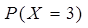 , если а=4.
, если а=4.
Решение: По формуле (9) при известных 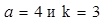 получим
получим
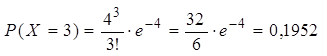
Теперь найдем числовые характеристики Х:
ü математическое ожидание 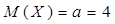
ü дисперсия 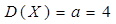
ü среднее квадратическое отклонение 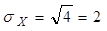
Ответ: 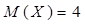
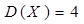
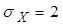
На практике, когда рассматриваются потоки событий в единицу времени Пуассоновское распределение рассматривают следующим образом – пусть имеется некоторая последовательность событий, наступающих в случайные моменты времени (это поток событий). Интенсивность потока – среднее число событий, появляющихся в единицу времени – λ. Пусть данный поток событий обладает следующими свойствами:
1) вероятность появления k событий за определенный промежуток времени зависит только от длины этого промежутка, но не от точки отсчета, т.е. интенсивность потока постоянная величина;
2) вероятность появления k событий в любом промежутке времени не зависит от того, появились события в прошлом или нет;
3) появления более одного события за малый промежуток времени практически не возможно.
При выполнении свойств 1- 3 данный поток событий обладает свойствами распределения Пуассона и тогда вероятность того, что за промежуток времени t событие произойдет k раз, равна
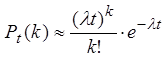 (13)
(13)
Пример 4: Среднее число вызовов, поступающих в сотовую компанию за 1 минуту, равно двум. Найти вероятность того, что за 4 минуты поступит а) четыре вызова, б) менее трех вызовов, в) не менее трех вызовов.
Решение: Исходя из условий задачи имеем дело с потоком событий, имеющих Пуассоновское распределение:
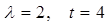
По формуле (13) найдем вероятности поступления 0, 1, 2, 3 или 4 звонка:
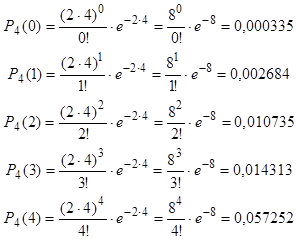
Теперь найдем искомые вероятности:
а) четыре вызова - 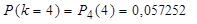
б) менее четырех вызовов

в) не менее четырех вызовов - 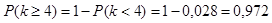
Ответ: 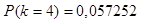
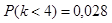
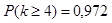
 2014-02-12
2014-02-12 10791
10791